Novocherkassk, Rostov-on-Don, Russian Federation
Novocherkassk, Rostov-on-Don, Russian Federation
from 01.01.2019 until now
Platov South-Russian State Polytechnic University (NPI) (Obscheinzhenernye discipliny, professor)
from 01.01.1980 to 01.01.2019
Moscow, Russian Federation
A mathematical model of a two-dimensional high-speed flow in terms of justification and taking into account several physical assumptions is formulated. The problem is solved analytically in the plane of the velocity hodograph and in the physical plane to determine all parameters in terms of flow flow. The coupling of a uniform flow with a general flow in the form of a "simple wave" made it possible to achieve a reduction in the error of the mathematical model. The adequacy of the pre-sented method is shown. The existing models are described that are insufficiently acceptable and adequate in terms of the geometry of the flow boundary, but with a large mismatch in local depths and velocities. The adequacy of the new model as a whole is characterized by the convergence of the model parameters both in geometry (flow spreading boundaries) and kinematics (depth and flow velocity) increased to 18% in both directions. The section of the "simple wave" should be well combined with the real flow, taking into ac-count the forces of resistance to the flow. The boundaries of the use of the proposed model belong to the section of the expansion of the flow in 3-7 b as required in the reference literature, and have been clarified in earlier works. The proposed model, as shown in the article, takes into account real (experimental) flow spreading and is consistent with previously performed theoretical studies. An important conclusion in the article is that the values of the Froude criterion in the new model can be any in the range from 1 to infinity, and at the same time the section "$X_D^I$" can increase with in-creasing Froude number.
mathematical model, 2D water flow, equations of motion, open channel hydraulics, analytical solution, simple wave
Введение
Объектом исследования являются двумерные плановые потоки, а именно, пространственные потоки, у которых значение скоростей и ускорений по какому-либо направлению пренебрежимо мало. И если это направление нормально к дну водовода, то такие водные потоки называются двумерными плановыми [1]. Необходимо отметить физические допущения для таких потоков [1, 2].
1. Поток в открытом русле, у которого ширина поверхности в несколько раз больше его глубины;
2. Рельеф дна достаточно плавный и искривление струй в плане не слишком велико. Это условие существенно, поскольку при большой кривизне струй образуются значительные перепады свободной жидкости и течение приобретает ярко выраженный пространственный характер.
3. Вертикальные составляющие местных осредненных скоростей и ускорений малы.
4. Векторы скоростей жидких частиц, расположенных на одной вертикали, лежат в одной плоскости.
5. Распределение скоростей на любой вертикали равномерное.
Предметом исследования является математическая модель течения открытого водного потока. Поток свободно растекается за водопропускной трубой прямоугольного сечения и находится в безнапорном режиме. В работе рассматриваются потенциальные в среднем, высокоскоростные потоки, у которых число Фруда больше единицы.
Открытый водный поток при выходе из отверстия может обладать скоростями, существенно превышающими допустимые скорости для неукрепленной части русла. Натурные исследования, выполненные в работах [2, 3], показывают, что основной причиной разрушений гидротехнических сооружений являются опасные размывы нижнего бьефа. Поэтому для расчета крепления отводящего русла проектировщикам ГТС необходима информация по параметрам потока в окрестности выходной кромки трубы (для расчета крепления отводящего русла).
Впервые задача плановой гидравлики поставлена Н.М. Бернадским, В.М. Маккавеевым и разработан один из приближенных методов решения для спокойных (докритических) потоков. Дальнейшее развитие теория плановых потоков получила в работах отечественных исследователей Н.Т. Мелещенко, Г.И. Сухомела, И.И. Леви, С.Н. Нумерова, Ф.И. Франкля, И.А.Шеренкова, Б.Т.Емцева, Л.И. Высоцкого и некоторых зарубежных ученых А.Т. Иппена, Х. Рауза, Д. Гарлемана, и др.
Теория и методы решения задач плановой гидравлики наиболее полно изложены в монографиях Г.И. Сухомела, И.И. Леви, Б.Т. Емцева [1], И.А. Шеренкова [2], В.Н. Коханено [3], В.А. Большакова [4], М.Д. Чертоусова [5].
Различают два основных типа инженерных задач плановой гидродинамики [2]. Первый тип или прямые задачи, в которых, помимо рельефа дна, задается конфигурация русла в плане, т.е. форма его берегов. Дополняя эти данные известными значениями скоростей и глубин в одном из граничных живых сечений, необходимо найти форму свободной поверхности и распределение скоростей в пределах выбранного участка водовода. Второй тип задач — обратные задачи, в которых задается закон изменения некоторых гидравлических параметров и отыскиваются другие параметры потока, а также геометрические характеристики русла (рельеф дна), формирующего указанный поток. При этом необходимо учитывать динамические особенности и свойства течения.
Математической основой указанных выше задач являются квазилинейные дифференциальные уравнения в частных производных. В подавляющем большинстве случаев, вследствие того, что характер движения сложен, получение аналитического решения затруднено.
Поэтому перспективным считается численно-аналитический подход к решению таких задач. Кроме того, приветствуется применение приближенных методов решения.
Известные ранее модели по свободному растеканию высокоскоростного потенциального в среднем потока можно разделить на три группы. Модели основанные на:
- обработке экспериментальных и натурных данных;
- использовании метода характеристик;
- использовании плоскости годографа скорости.
К недостаткам известных моделей можно отнести следующие. Результаты расчетов по модели первой группы могут быть использованы в определенных рамках проведенных экспериментов.
Одним из самых известных методов расчёта параметров высокоскоростного потока является метод И.А. Шеренкова с использованием универсального графика [2], построенного на основе метода характеристик. Однако для практического использования график обладал недостаточной адекватностью. Расхождения между расчетными и экспериментальными значениями достигали 50%. Дальнейшее развитие метод характеристик получил в работах [7-18].
В аналитическом методе, предлагаемом авторами и основанном на использовании плоскости годографа скорости, достигнута погрешность до 20%. Метод хорошо себя зарекомендовал. Однако в моделях раннего периода не учитывалось наличие инерционного фронта и известные положения теории сопряжения равномерного потока с течением общего вида. Не учитывались простые волны в потоке, следовательно не совсем корректно ставилась граничная задача, исходя из известных положений.
Актуальность работы. Результаты работы являются важным этапом в развитии аналитических методов по течению двухмерных в плане открытых водных потоков, а также по сопряжению различных участков потока. Работа является востребованной при проектировании гидротехнических сооружений, в которых водные потоки близки к двухмерным в плане [13-35].
Целью работы является получение аналитического решения задачи построения крайней линии тока при свободном растекании высокоскоростного, потенциального, стационарного, открытого водного потока. При этом требуется определение комплекса параметров высокоскоростного потока за безнапорным отверстием.
Методы решения задачи
Поставленная задача решается аналитически, а также с использованием пакетов прикладных программ [19-21]. Задачу определения границы растекания высокоскоростного потока разобьём на этапы.
1. Выбор схемы растекания потока из накопленных ранее теоретической и экспериментальной информации.
2. Вывод зависимостей для параметров потока.
3. Определение параметров потока вдоль характеристики 1-го семейства в точках ее пересечения с линиями тока с расходом.
4. Определение параметров потока в области течения общего вида.
5. Вывод параметрического уравнения для границы потока.
6. Подтверждение адекватности полученной математической модели реальному потоку.
Рассмотрим свободное растекания бурного потока в широкое гладкое горизонтальное отводящее русло за безнапорной трубой, см. рис. 1. В реальных потоках вследствие сил инерции, сил тяжести и сил сопротивления потоку он принимает форму «лепестка растекания» [1-5]. Для потенциальных высокоскоростных потоков в окрестности выхода потока из трубы, подающей воду, силами сопротивления потоку можно пренебречь [1].
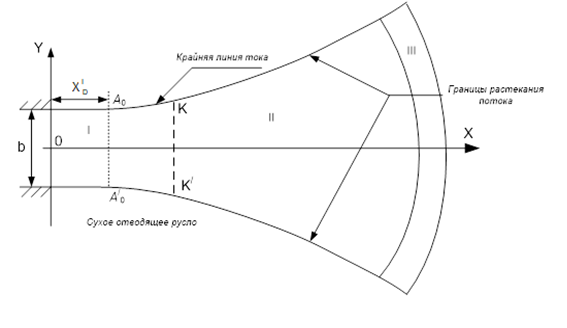
Рис. 1. Схема модели растекания потока: I – участок равномерного течения
(τ=τ_0, $\theta$=0); II – участок переходного основного течения потока;
III – участок радиального течения потока
Проведем анализ интегральных уравнений движения потока.
Уравнение сохранения напора:
$H_0=u^2/2g+h$, (1)
где $H_0=(u_0^2)/2g+h_0$ – постоянная величина; h – местная глубина потока (средняя по сечению); u - местная скорость потока (средняя по сечению); g – ускорение силы тяжести.
Уравнение неразрывности потока:
Q=Buh, (2)
где B – ширина потока.
Введем в системе уравнений (1), (2) параметр $τ=u^2/(2gH_0 )$, который связан с критерием Фруда формулой [1]:
$F=\frac{2τ}{1-τ}$, (3)
F и τ – это параметры, характеризующие кинетичность потока, причем F∈(1,∞), τ∈(1/3,1 для бурных потоков.
Тогда глубину и скорость потока можно выразить через его кинетичность [3]:
$h=H_0$ (1-τ); $u=τ^{1/2} \sqrt{2gH_0}$. (4)
С учетом соотношения (3) систему уравнений (1) и (2) перепишем в виде:
$ \begin{cases}
Q=BH_0 τ^{1/2} \sqrt{2gH_0}(1-τ);\\
h=H_0 (1-τ), u=τ^{1/2} \sqrt{2gH_0}
\end{cases} $ (5)
Исходя из системы равенств (5) и пользуясь известным фактом из гидравлики открытых потоков [1, 3] получим очевидный вывод: бурный поток входя в расширение расширяется и его кинетичность увеличивается. Следовательно в пределе при τ→1 получаем:
$B→∞; h→0; u→u_{max}=\sqrt{2gH_0}$ . (6)
Уравнение характеристики 1-го семейства, выходящей из точки $М_0$ (см. рис. 2), которая принадлежит 1-му участку, имеет вид [1]:
$\theta(τ)=\sqrt{3}arctg\sqrt{\frac{3τ-1}{3(1-τ)}}-arctg \begin{pmatrix}\sqrt{\frac{3τ-1}{1-τ}}+C_1 \end{pmatrix}$ (7)
где $C_1-arctg\sqrt{\frac{3τ_0-1}{1-τ_0}}-\sqrt{3}·arctg \begin{pmatrix}\sqrt{\frac{3τ_0-1}{1-τ_0}}+C_1 \end{pmatrix}$.
При τ→1 имеем
$θ→θ_{max}=C_1+\frac{π}{2}(\sqrt3-1)$.
Известно также [1], что волновой угол (угол между линией тока и характеристикой) $ α=arcsin\sqrt{\frac{1-τ}{2τ}}$ при τ→1 стремится к нулю. Таким образом определяем максимальный угол растекания θmax.
Тогда к условиям (6) необходимо добавить условие предельного угла растекания
$B→∞; h→0; u→u_{max}=\sqrt{2gH0}, θ→θ_{max} . $ (8)
Совокупность условий (8) соответствует участку III на рис. 1 — поток стремится к радиальному потоку. Следовательно задача по определению геометрических и кинематических параметров вдоль границы растекания потока сводится к задаче сопряжения равномерного потока с радиальным потоком.
Выбор схемы растекания потока из накопленных ранее теоретической и экспериментальной информации
Исходя из общих положений теории плановой гидравлики [1-5], сопряжение равномерного потока (I) с радиального растекающимся (IV) возможно только с наличием четырехугольного участка «простые волны» (II), см. рис.2.
Вывод зависимостей для параметров потока
На участке I параметры потока u0, h0, b/2 не изменяются. Точка M0 принадлежит характеристике 1-го семейства с параметрами t0, q=0. Волновой угол в этой точке равен
$a_0=arcsin\sqrt{\frac{1-t_0}{2t_0}}$.
Из теории двухмерных в плане бурных потоков [1] известно, что вдоль характеристики 2-го семейства справедливо равенство
$\frac{dy}{dx}=tg(q-a)$.
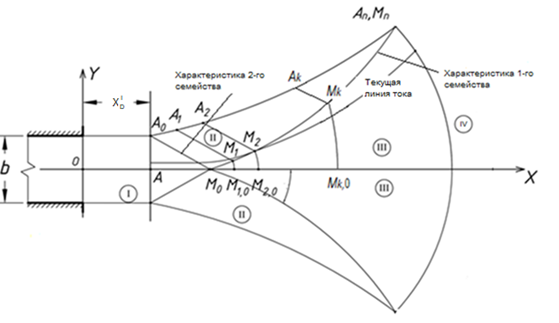
Рис. 2. Схема модели растекания потока по участкам:
I – равномерного течения; II – простых волн; III - общего вида;
IV – радиального растекания потока; $X_D^I$ – длина инерционного фронта; M0, M1,…, Mn – характеристика 1-го семейства;
A0M0, A1M1,…, АnMn – характеристики 2-го семейства (отрезки прямых линий);
u0, h0, b/2 – параметры потока на выходе из трубы (скорость, глубина, ширина), подающей воду
Так как q=0; a=a0, M0A/0 и M0A0 прямые линии, четырехугольник на рис. 3 является прямоугольной трапецией. Таким образом при известном расстоянии $X_D^I$ определяется геометрия и кинематика I-го участка растекания потока.
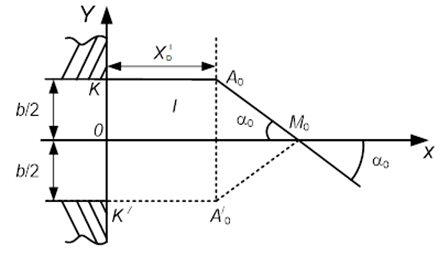
Рис. 3. Схема участка равномерного растекания потока
Для определения параметра $X_D^I$ воспользуемся формулой, приведенной в работах [11-12]
$X_D^I=trunc
\begin{bmatrix}\frac{\sqrt{F_0-1}}{sinθ_{max}(F_0+2)}h_0
\end{bmatrix}+1$ , (9)
где 1 – означает единицу измерения глубины h0. В расчетах это 1 см, в натурных экспериментах — 1 м. Формула (9) выведена из составления структурной формулы и определения коэффициентов методом регрессионного анализа. Для вывода этой формулы была использована информация 70 экспериментов, часть которых опубликована в работе [3].
На участке III, в области течения общего вида, в плоскости годографа скорости линии тока имеют вид
$\Psi=A\frac{sinθ}{τ^{1/2}}=const$, а функция тока $\Psi=\Psi(τ,θ)$ (10)
и удовлетворяют уравнению в частных производных
$\frac{\delta}{\deltaτ}\left\{\frac{2τ}{1-τ}\frac{\delta\psi}{\deltaτ}\right\}+\frac{1-3τ}{2τ(1-τ)^2}\frac{\delta\psi}{\deltaθ}=0$, (11)
приведенному в работе [3]. Соответствующие эквипотенциали выражаются формулой
$\varphi=A\frac{h_0}{H_0}\frac{cosθ}{τ^{1/2}(1-τ)}=const$, а потенциальная функция $\varphi=\varphi(τ,θ)$. (12)
Функция тока (10) и потенциальная функция (12) удовлетворяют системе уравнений в плоскости годографа скорости [1, 3]
$ \begin{cases}
\frac{\delta\varphi}{\deltaθ}=\frac{2h_0}{H_0}\frac{τ}{1-τ}\frac{\delta\varphi}{\deltaτ}\\
\frac{\delta\varphi}{\deltaθ}=\frac{h_0}{2H_0}\frac{3τ-1}{1-τ^2}\frac{\delta\psi}{\deltaθ}
\end{cases}$
При этом справедливы равенства (4) для местных скоростей и глубин.
Одним из решений уравнения (11) является функция
$\psi(τ,θ)=A\frac{sinθ}{τ^{1/2}}$, (13)
которая подходит для описания поведения бурного потенциального в среднем водного потока вдоль линии тока.
В выражении (13): $A=\frac{u_0b}{2sinθ_{max}}$ - постоянная для всего потока [3]; sinθ - функция, возрастающая вниз по течению потока; τ - параметр кинетичности потока также возрастает вниз по течению. Следовательно вдоль фиксированной линии тока (функция (13)) может удовлетворяться условие:
$\psi(τ,θ)=A\frac{sinθ}{τ^{1/2}}=const$.
Линия тока отсекает расход, определяемый коэффициентом K:
QK=KQ ,
где Q – общий расход потока.
Общий расход Q, отнесенный к начальной глубине потока h0 (для верхней части потока относительно оси OX) равен
$Q=u_0\frac{b}{2}=\frac{QK}{2}$ .
Тогда, с учетом выражения (10) получаем зависимость между параметрами потока на участке III вдоль линии тока с расходом, определяемым коэффициентом K:
$\frac{sinθ}{τ^{1/2}}=Ksinθ_{max}, K=\frac{Q_K}{Q}$.
Определение параметров потока в области течения общего вида
1) В плоскости годографа скорости для определения параметров q, t в точке пересечения произвольной линии тока и произвольной эквипотенциали необходимо решить систему уравнений:
$\begin{cases}
A\frac{sin\theta}{\tau^{1/2}}=Ksin\theta_{max};\\
\frac{cos\theta}{\tau^{1/2}(1-\tau)}=\frac{cos\theta_x}{\tau_x^{1/2}(1-\tau_x)}
\end{cases}$ (14)
где K задано; θx, τx – параметры в точке пересечения характеристики первого семейства с линией тока, определяемой коэффициентом расхода K.
Решение системы (14) сводится к решению кубического уравнения [3].
2) Определение координат потока на участке III. Для решения этой задачи воспользуемся дифференциальной связью [3]:
$dx+idy=(dφ+i\frac{h_0}{h}d\psi)\frac{1}{V}e^{iθ}$ (15)
где i – комплексная единица; V – модуль скорости жидкой частицы потока.
Из выражения (15) вдоль линии тока справедливы дифференциальные связи
$dx=\frac{dφ}{V}cosθ;$ $dy=\frac{dφ}{V}sinθ$,
причем
$V=τ^{1/2}\sqrt{2gH_0}; sinθ=K(τ)τ^{1/2}sinθ_{max}; cosθ=\sqrt{1-K^2(τ)τsin^2θ_{max}}.$
Далее интегрированием уравнений (16) определяются координаты X(τ), Y(τ) как приведено в работе [3].
Таким образом на участке потока III (течения общего вида) все параметры потока определяются:
- геометрия потока, т.е. координаты жидкой частицы X(τ), Y(τ);
- параметр кинетичности τ;
- угол θ(τ) наклона вектора скорости к оси симметрии потока Ox;
- величина скорости V(τ);
- глубина потока h(τ).
Определение параметров потока τ, θ вдоль характеристики 1-го семейства в точках ее пересечения с линиями тока расходом, определяемым коэффициентом K
Решая совместно уравнения (7) и (10), определяем коэффициент K как функцию τ:
$K(τ)=\frac{sinθ(τ)}{τ^{1/2}sinθ_{max}}$ . (17)
Задавая параметр τ из уравнения (7) определяем угол q(t), а из уравнения (17) - Kτ .
Параметры τ, θ изменяются вдоль характеристики 1-го семейства, но не изменяются в простых волнах – участок II (от характеристики 1-го семейства до границы потока). Иначе, в плоскости годографа скорости границы потока и характеристики 1- го семейства имеют один и те же вид.
Так как характеристики 2-го семейства прямые линии с постоянными параметрами τ, θ, то в точках пересечения их с границей потока A0, A1,…,An они будут также иметь значения параметров τ, θ.
Для построения крайней линии тока необходимо в точке Мi выбрать пару τ i, θ i и перенести их значения до формирования крайней линии тока в точке Аi, а направление взять вдоль соответствующей линии тока, проходящей через эти точки на характеристике, см. рис. 2.
Вывод параметрического уравнения для границы потока
Используя функции (10), (12) и уравнение связи (15), выражения (16) примут вид
$ dx=\frac{\sqrt{1-K^2(τ)τsinθ_{max}}}{τ^{1/2}\sqrt{2gH_0}}dφ; dy=\frac{K(τ)sinθ_{max}}{\sqrt{2gH_0}}dφ. $ (18)
Потенциальная функция, проходящая через точку τ, θ преобразуется в функцию одной переменной τ:
$ φ(τ,θ)=A\frac{h_0}{H_0}\frac{cosθ}{τ^{1/2}(1-τ)}=A\frac{h_0}{H_0}\frac{\sqrt{1-K2(τ)τsin^2θ_{max}}} {τ^{1/2}(1-τ)}=φ(τ). $ (19)
Из второго уравнения системы (18) и соотношения (17) получим, что
$d[y(τ)]=\frac{K(τ)sinθ_{max}}{\sqrt{2gH_0}}dφ=\psi_1(τ)dτ.$ (20)
Интегрируя (20) с учетом $yτ_0=\frac{b}{2}$, получим совокупность ординат точек потока на его крайней линии
$\psi_1(τ)=\frac{K(τ)sinθ_{max}}{\sqrt{2gH_0}}\frac{dφ}{dt};$ $Y(τ)=\frac{b}{2}+\int_{τ_0}^τ\psi_1(t)dt.$ (21)
Аналогично интегрируя первое уравнение системы (18), получим абсциссы точек потока
$φ(τ)=A\frac{h_0}{H_0}\frac{\sqrt{1-K^2(τ)sinθ_{max}}} {τ^{1/2}(1-τ)}\frac{dφ}{dt};$ $X(τ)=X_D^I+\int_{τ_0}^τφ(t)dt.$ (22)
Интегралы (21), (22) рассчитывались с помощью ППП MathCad.
В частном случае при K=1 из выражения (19) следует:
$d[y(τ)]=\frac{sinθ_{max}}{\sqrt{2gH_0}}dφ,$
где $φ(τ)=A\frac{h_0}{H_0}\frac{cosθ}{τ^{1/2}(1-τ)};$
$Y(τ)=\frac{b}{2}+\frac{sinθ_{max}}{\sqrt{2gH_0}}A\frac{h_0}{H_0}\int_{τ_0}^τ\frac{\sqrt{1-τsin^2θ_{max}}}{ t^{1/2}(1-t)}dt,$
что соответствует теории плановых потоков [1-3].
Скорости и глубины вдоль граничной линии тока при известном t определяются по формулам (4).
Результаты моделирования и их обсуждение
Рассмотрим числовой пример моделирования для свободно растекающегося водного потока в безнапорном режиме за водопропускной трубой прямоугольного сечения со следующими параметрами:
- начальная скорость потока V0=147.7 [см/с];
- начальная глубина потока относительно дна h0=9.27 [см];
- ускорение свободного падения g=981 [см2/с];
- ширина трубы b=16 [см].
Экспериментальные данные заимствованы в работе [3] и для крайней линии тока (в сантиметрах) имеют вид:
$\begin{matrix}
X_Э=(0&4&24&44&64&71)&;\\
Y_Э=(b/2&9.5&32&59&76&80 .
\end{matrix}$
1) Находим кинематику и геометрию I участка растекания потока:
- число Фруда F0=2.397 ;
- гидродинамический напор H0=20.4 м ;
- начальную кинетичность потока τ0=0.545 ;
- волновой угол в точке выхода потока из трубы α0=0.702 p или α0=40°23 ;
- угол наклона вектора скорости потока жидкости к оси ОХ на бесконечности θmax=0.981 p или θmax=56°23 .
- длину инерционного фронта $X_D^I=3$ см ;
- расстояние по оси симметрии потока от конца инерционного участка до точки M0
A0M0=9.46 см ; - длину прямолинейного отрезка характеристики второго семейства между точками A0 и M0 A0M0=1.24 см .
2) Разобьем верхнюю половину трубы на равные отрезки и вычислим коэффициенты расхода K на намеченных линиях тока. Определим параметры потока в точках пересечения конкретной линии тока с характеристикой первого семейства τM, θM . Эти параметры переносим на крайнюю линию тока по простой волне.
3) Вычисляем кинетичность τос потока в точках на оси симметрии при пересечении соответствующей линии тока и эквипотенциали.
4) Строим сетку параметров внутри области общего течения. Линия тока задается коэффициентом расхода, а эквипотенциаль – параметром кинетичности на оси симметрии. Результаты вычислений сведены в таблицу 1.
5) Вычисляем интегралы (21), (22) для получения координат точек потока. Результаты вычислений сведены в таблицу 2.
На рисунке 4 приведен график линий тока и эквипотенциалей потока, построенных по результатам числового расчета.
Выводы
1. В работах [6-18] была предложена модель приемлемой (до 20%) адекватности по геометрии границы растекания потока, но с большим рассогласованием по местным глубинам и скоростям. Адекватность в целом характеризуется сходимостью параметров модели как по геометрии (границы растекания потока), так и по кинематике (глубины и скорости потока). В данной работе авторами достигнута адекватность в пределах до 18% по обоим направлениям.
2. Участок «простые волны», как будет показано в следующих работах, хорошо сочетается с реальным потоком при учете сил сопротивления потоку.
3. Границы пользования моделью принадлежат участку расширения потока $\beta=3\div7$ как это требуется в справочной литературе, и уточнены в работах [4,5].
Таблица 1.
Параметры потока в области его растекания
|
№ шага |
K |
|
|
|
|---|---|---|---|---|
|
0 |
0 |
0.545 |
0 |
0.545 |
|
1 |
0.025 |
0.559 |
0.016 |
0.559 |
|
2 |
0.05 |
0.574 |
0.031 |
0.573 |
|
3 |
0.075 |
0.588 |
0.048 |
0.587 |
|
4 |
0.1 |
0.602 |
0.065 |
0.601 |
|
5 |
0.125 |
0.616 |
0.082 |
0.615 |
|
6 |
0.15 |
0.631 |
0.099 |
0.628 |
|
7 |
0.175 |
0.645 |
0.117 |
0.642 |
|
8 |
0.2 |
0.66 |
0.135 |
0.655 |
|
9 |
0.225 |
0.674 |
0.154 |
0.669 |
|
10 |
0.25 |
0.688 |
0.173 |
0.682 |
|
… |
… |
… |
… |
… |
|
25 |
0.625 |
0.892 |
0.513 |
0.875 |
|
26 |
0.65 |
0.904 |
0.539 |
0.887 |
|
27 |
0.675 |
0.915 |
0.567 |
0.899 |
|
28 |
0.7 |
0.926 |
0.594 |
0.91 |
|
29 |
0.725 |
0.936 |
0.623 |
0.921 |
|
30 |
0.75 |
0.946 |
0.651 |
0.932 |
|
31 |
0.775 |
0.955 |
0.681 |
0.942 |
|
32 |
0.8 |
0.964 |
0.711 |
0.952 |
|
33 |
0.825 |
0.972 |
0.742 |
0.961 |
|
34 |
0.85 |
0.979 |
0.774 |
0.97 |
|
35 |
0.875 |
0.985 |
0.806 |
0.978 |
|
36 |
0.9 |
0.99 |
0.84 |
0.985 |
|
… |
… |
… |
… |
… |
Таблица 2.
Координаты потока в области его растекания (в метрах)
|
№ шага |
|
|
|
|
|
|
|
|---|---|---|---|---|---|---|---|
|
0 |
12.457 |
0 |
0 |
0 |
8 |
8 |
0 |
|
1 |
12.701 |
9.545 |
|
|
9.457 |
9.5 |
0.455 |
|
2 |
12.963 |
9.643 |
|
|
10.304 |
|
|
|
3 |
13.243 |
9.75 |
|
|
11.467 |
|
|
|
4 |
13.542 |
9.868 |
|
|
12.638 |
|
|
|
5 |
13.864 |
9.997 |
|
|
13.818 |
|
|
|
6 |
14.208 |
10.137 |
|
|
14.009 |
|
|
|
7 |
14.578 |
10.29 |
|
|
15.211 |
|
|
|
8 |
14.976 |
10.458 |
|
|
16.425 |
|
0 |
|
9 |
15.406 |
10.64 |
|
|
17.653 |
|
|
|
10 |
15.87 |
10.839 |
|
|
17.897 |
|
|
|
… |
… |
… |
… |
… |
… |
|
… |
|
25 |
32.967 |
18.501 |
|
|
26.419 |
|
|
|
26 |
35.837 |
19.812 |
|
|
27.862 |
|
|
|
27 |
39.285 |
21.395 |
|
|
29.611 |
|
|
|
28 |
43.492 |
23.337 |
24 |
2.761 |
32.771 |
38 |
15.958 |
|
29 |
48.723 |
25.767 |
|
|
34.496 |
|
|
|
30 |
55.373 |
28.878 |
|
|
38.021 |
|
|
|
31 |
64.057 |
32.975 |
|
|
42.723 |
|
|
|
32 |
75.763 |
38.552 |
|
|
49.222 |
|
|
|
33 |
92.256 |
46.495 |
44 |
5.671 |
58.644 |
59 |
0.607 |
|
34 |
116.791 |
58.462 |
64 |
8.654 |
73.13 |
76 |
3.924 |
|
35 |
156.291 |
77.997 |
71 |
9.855 |
97.332 |
80 |
17.807 |
|
36 |
226.119 |
113.119 |
|
|
122.085 |
|
|
|
… |
… |
… |
… |
… |
… |
… |
… |
4. Модель учитывает реальные (экспериментальные) растекания потока и согласуется с ранее накопленными теоретическими исследованиями [32-37].
5. Значения критерия Фруда в модели могут быть любыми F0∈(1, ∞) . В зависимости от этого участок «XDI » может увеличиваться с возрастанием числа Фруда F0.
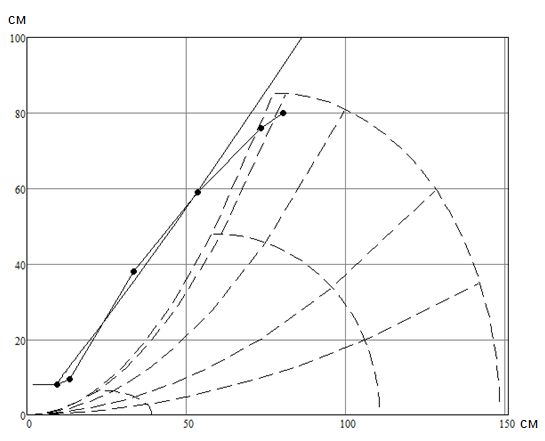
Рис. 4. Результаты числового расчета определения границы растекания потока
(граница потока – сплошная линия;
граница потока по экспериментальным данным - точки;
линии тока и эквипотенциали – пунктирные линии)
1. Yemtsev, B.T. Two-dimensional stormy streams. Moscow: Energiya Publ., 1967. 212 P. (in Rus-sian).
2. Sherenkov, I.A. On the planned problem of spreading a jet of a turbulent flow of an incompress-ible liquid. News of the Academy of Sciences of the USSR. 1958, № 1. - Pp. 72-78. (in Rus-sian)
3. Kokhanenko, V.N. Modeling of stormy two-dimensional in terms of water flows. Rostov-on-Don: Yuzhnij federal‘nij universitet Publ., 2013. 180 P. (in Russian).
4. Bolshakov, V.A. Handbook of hydraulics. Kiev: Higher school, 1984. 343 p. (in Russian).
5. Chertousov, M.D. Hydraulics. Special course. - M.-L.: Gosenergoizdat, 1962. - 624 P. (in Rus-sian)
6. Aleksandrova, M.S. The method of analogies between the hydraulics of two-dimensional in terms of water flows and gas dynamics. Construction and Architecture. 2020. Vol. 8. Issue 2(27). Pp. 49-52. DOI:https://doi.org/10.29039/2308-0191-2020-8-2-49-52. (in Russian). EDN: https://elibrary.ru/QNQOGB
7. Duvanskaya, E.V. Solving the problem of coupling calm water flows in rectangular channels of various widths with the expansion of the channel and taking into account the friction forces. Ecology, economics, technologies and equipment. Rostov-on-Don, 2002. Pp.163-172. (in Rus-sian).
8. Kosichenko, Yu.M. Analysis of the study and refinement of methods of free flow spreading be-hind non-pressurized culverts VESTNIK of Samara University. 2011. Issue 9. Pp. 27-33. http://www.sgau.ru/izdatelstvo/vestnik (in Russian).
9. Papchenko, N.G. Determination of the equation of the extreme current line in the plane of the velocity hodograph in the problem of free spreading of a turbulent flow behind pressure-free pipes. Science journal Bulletin of higher education institutes North Caucasus region. Techn. sci-ence. 2013. 3. Pp. 53-54. ISSN 0321-2653 (in Russian). EDN: https://elibrary.ru/QITKPB
10. Papchenko, N.G. General technology for solving practical problems of hydraulics of two-dimensional in terms of stationary turbulent water flows by an analytical method using the plane of the velocity hodograph. Scientific journal Proceeding of Voronezh State University. Series: Phisics. Mathematics. 2014. Pp. 159-163. (in Russian).
11. Kokhanenko, V.N., Kondratenko, A.I., Kosichenko M.Yu., Lidnevskij, V.I., Kelekhsaev, D.B. Solving the problem of free flow spreading behind non-pressurized culverts. Science journal Bulletin of higher education institutes North Caucasus region. Natural science. 2017. 2 (194). Pp. 12-25. DOIhttps://doi.org/10.23683/0321-3005-2017-2-15-25 (in Russian). EDN: https://elibrary.ru/ZAFAPJ
12. Kelekhsaev, D. B., Kondratenko, A.I., Evtushenko S.I. A System of Equations for Potential Two-Dimensional In-Plane Water Courses and Widening the Spectrum of Its Analytical Solutions. AIP Conference Proceedings, 2019. 2188, 050017. DOI:https://doi.org/10.1063/1.5138444 EDN: https://elibrary.ru/GSOFUL
13. Aleksandrova, M.S. Simple waves in the theory of two-dimensional in terms of water flows and the scheme of their use for free flow spreading. Construction and Architecture. 2020. Vol. 8. Is-sue 3. Pp. 47-50. DOI:https://doi.org/10.29039/2308-0191-2020-8-3-47-50. (in Russian). EDN: https://elibrary.ru/BUVVRF
14. Kokhanenko, V.N., Aleksandrova, M.S., Kondratenko, A.I. A model of the process of free prop-agation of a two-dimensional water flow behind pressure-free openings. Vestnik MGSU. 2021. 16(1). Pp. 67-74. DOI:https://doi.org/10.22227/1997-0935.2021.1.67-74. (in Russian). EDN: https://elibrary.ru/SVXXOL
15. Burtseva, O.A., Aleksandrova, M.S., Kondratenko, A.I. Solving the problem of free spreading of a turbulent two-dimensional water flow when flowing out of a pressure-free pipe. Construction and Architecture. 2021. Vol. 9 Issue 2. Pp. 21-25. DOI:https://doi.org/10.29039/2308-0191-2021-9-2-21-25. (in Russian). EDN: https://elibrary.ru/JGAGUR
16. Aleksandrova, M.S., Kondratenko, A.I. Determination of the parameters of the limiting expan-sion of the flow in the problem of free spreading of a turbulent flow. Construction and Archi-tecture. 2021. Vol. 9. Issue 2(31). Pp. 16-20. DOI:https://doi.org/10.29039/2308-0191-2021-9-2-16-20. (in Russian). EDN: https://elibrary.ru/NHKDNL
17. Kondratenko, A.I., Aleksandrova, M.S. Estimation of a motion equations system of a potential two-dimensional in a water flow plan to dimensionless form. IOP Conference Series: Materials Science and Engineering. "VII International Scientific Conference "Integration, Partnership and Innovation in Construction Science and Education", IPICSE 2020" 2021. No. 012122. DOI: https://doi.org/10.1088/1757-899X/1030/1/012122; EDN: https://elibrary.ru/NNMOOG
18. Burtseva, O.A., Kokhanenko, V.N., Evtushenko, S.I., Alexandrova, M.S. The model of free spreading a flow rapid behind a rectangular pipe. International Journal for Computational Civil and Structural Engineering. 2022. 18(2). Pp. 74-84. DOIhttps://doi.org/10.22337/25879618-2022-18-2-74-84. DOI: https://doi.org/10.22337/2587-9618-2022-18-2-74-84; EDN: https://elibrary.ru/GXINFK
19. Papchenko N.G. Certificate of Registration of Computer Programs, Federal Institute of Indus-trial Property (FIPS) No. RU 2014611308, 2014, Russia. Available online: https://www1.fips.ru/ ofpstorage/Doc/PrEVM/RUNWPR/000/002/022/618/552/2014611308-00001/
20. Burtseva, O.A. Determination of Parameters of a Freely Spreading Flow. Certificate of Registra-tion of Computer Programs, Federal Institute of Industrial Property (FIPS) No. RU 2022618552, 2022, Russia. Available online: https://www1.fips.ru/ ofpstor-age/Doc/PrEVM/RUNWPR/000/002/022/618/552/2022618552-00001/ (accessed on 1 July 2023)
21. Aleksandrova, M.S. Determination of Parameters of Flow along the extreme current line. Certif-icate of Registration of Computer Programs, Federal Institute of Industrial Property (FIPS) No. RU 2022666655, 2022, Russia. Available online: https://www1.fips.ru/ ofpstor-age/Doc/PrEVM/RUNWPR/000/002/022/618/552/2022666655-00001/ (accessed on 1 July 2022)
22. Tang, S. L., Antonia, R. A., Zhou, Y. Transport equation for the mean turbulent energy dissipa-tion rate on the centerline of a fully developed channel flow. Journal of Fluid Mechanics. 2015. DOI:https://doi.org/10.1017/jfm.2015.342. EDN: https://elibrary.ru/STINRJ
23. Anderson, W., Barros, J.M., Christensen, K.T. & Awasthi, A. Numerical and experimental study of mechanisms responsible for turbulent secondary flows in boundary layer flows over span wise heterogeneous roughness. Journal of Fluid Mechanics. 2015. 768, Pp. 316-347. DOI:https://doi.org/10.1017/jfm.2015.91.
24. Aranda, J.Á., Beneyto, C., Sánchez-Juny, M., Bladé, E. Efficient Design of Road Drainage Sys-tems. Water, 2021. 13. 1661. DOI.org/10.3390/w13121661
25. Marcos Sanz-Ramos, Ernest Bladé, José Luis Aragón-Hernández. Interpreting the manning roughness coefficient in overland flow simulations with coupled hydrological-hydraulic distrib-uted models. Water. 2021. (Switzerland). DOI:https://doi.org/10.3390/w13233433.
26. Anees, M.T. et all. One- and Two-Dimensional Hydrological Modelling and Their Uncertainties. Flood Risk Manag. 2017, 11, 221-244. DOI:https://doi.org/10.5772/intechopen.68924
27. Nematollahi, B., Abedini, M.J. Analytical Solution of Gradually Varied Flow Equation in Non-prismatic Channels. Iranian Journal of Science and Technology - Transactions of Civil Engineer-ing. 2020. 44(1). DOI:https://doi.org/10.1007/s40996-019-00316-5.
28. Hager, W., Castro-Orgaz, O. Transcritical Flow in Open Channel Hydraulics: From Böss to De Marchi Journal of Hydraulic Engineering. 2016. 142(1). DOI:https://doi.org/10.1061/(asce)hy.1943-7900.0001091.
29. Hager, W. Unconfined Expansion of Supercritical Water Flow. Journal of Engineering Mechan-ics. 1997. 123(5) Pp. 451-457. DOI https://doi.org/10.1061/(asce)hy.1943-7900.0001091
30. Liu, J. L., Wang, Z. Z., Zhao, Y. F. Explicit equations for critical depth in open channels with complex compound cross sections. Flow Measurement and Instrumentation. 2012. DOI:https://doi.org/10.1016/j.flowmeasinst.2011.12.005.
31. Hubert, Chanson Explicit equations for critical depth in open channels with complex compound cross sections: A discussion. Flow Measurement and Instrumentation. 2013. DOI:https://doi.org/10.1016/j.flowmeasinst.2012.10.006.
32. Castro-Orgaz, O, Cantero-Chinchilla, F.N. Non-linear shallow water flow modelling over to-pography with depth-averaged potential equations. Environmental Fluid Mechanics 2020. DOI:https://doi.org/10.1007/s10652-019-09691-z EDN: https://elibrary.ru/STHVPF
33. Li, J, Li, S.S. Near-bed velocity and shear stress of open-channel flow over surface roughness. Environmental Fluid Mechanics. 2020. DOI:https://doi.org/10.1007/s10652-019-09728-3 EDN: https://elibrary.ru/IECTJP
34. Jesusdhas V., Balachandar R., Wang H., Murzyn F. Modelling hydraulic jumps: IDDES versus experiments. Environmental Fluid Mechanics. 2020. DOI:https://doi.org/10.1007/s10652-019-09734-5
35. Leng, X., Chanson, H. Hybrid modelling of low velocity zones in box culverts to assist upstream fish passage. Environ Fluid Mech. 2020. DOI:https://doi.org/10.1007/s10652-019-09700-1. EDN: https://elibrary.ru/AXSAPI
36. Yesin A.I. Problems of technical fluid mechanics in natural coordinates. Saratov, 2003. 144 P. (in Russian). EDN: https://elibrary.ru/TDMQSL
37. Yesin A.I. To the question of the unsteady flow of water in an open channel. Improvement of methods of hydraulic calculations of culverts and sewage treatment plants.2016. Issue 1(42), Pp. 12-19. (in Russian).






















