from 01.01.2015 until now
Russian Federation
Rostov na donu, Rostov-on-Don, Russian Federation
from 01.09.2014 until now
Kazan (Volga) Federal University (Institute of Design and Spatial Arts, Chief Researcher)
Bataysk, Rostov-on-Don, Russian Federation
The article presents a numerical and analytical solution to the problem of optimizing compressed rods according to the criterion of the maximum critical load with a possible loss of stability in two planes. We consider a wooden bar of rectangular cross section, the height of which varies according to a linear law, and the width is constant. The calculation is performed in an elastic formulation. A constraint on the constancy of the rod mass is introduced. Variable parameters are the ratio of the minimum section height to the maximum, as well as the ratio of the section width to the maximum height. Numerical search for the optimal solution is performed in the MATLAB environment using the method of sequential quadratic programming. It has been established that the use of rods with a cross-sectional height that varies linearly along the length is effective only if the rod is fixed in at least one of the planes according to the “pinched-free end” scheme. It has been established that the increase in the critical load when using rods with a linearly varying cross-sectional height can be up to 22%.
rod, wood, stability, optimization, sequential quadratic programming.
Введение
Древесина на протяжении многих веков является одним из основных конструкционных материалов в строительстве, что обусловлено ее высокими физико-механическими и техническими качествами. На современном этапе развития строительной отрасли в области проектирования и возведения зданий и сооружений с использованием конструкций из дерева имеет место значительный прогресс благодаря применению клееных деревянных конструкций [1-3].
Для совершенствования проектных решений и снижения материалоемкости строительства требуется разработка и развитие научно-обоснованных методов расчета и оптимизации строительных конструкций. Во многих конструкциях используются элементы с постоянной по длине геометрией поперечного сечения, однако из соображений уменьшения расхода материала в некоторых случаях целесообразно применять элементы переменной жесткости [4-6].
Постановка задачи о наивыгоднейшем очертании колонны принадлежит Ж.Л. Лагранжу. Подробный обзор аналитических решений задачи Лагранжа представлен в работах А.П. Сейраняна [7-8]. Особенностью аналитических решений задачи оптимизации сжатой колонны является наличие точек с нулевой площадью, где будут возникать бесконечные напряжения. Таким образом, для создания реальных конструкций эти решения неприменимы.
Решение с учетом ограничения на минимальную площадь поперечного сечения может быть выполнено с использованием численных методов. Численные решения задач оптимизации сжатых стержней приведены в работах [9-13]. В указанных публикациях найденная оптимальная форма стержня описывается нелинейной функцией, что затрудняет практическую реализацию таких решений, особенно в случае использования дерева в качестве конструкционного материала. Представляет интерес решение задач оптимизации стержней с линейно меняющейся высотой поперечного сечения и определение области их эффективного использования.
Методы
Рассматривается упругая деревянная стойка прямоугольного поперечного сечения, ширина которой постоянна и равна b, а высота меняется от h0 до βh0 по линейному закону (рис. 1). Стойка сжимается силой F. В качестве варьируемых параметров примем высоту h0, отношение β, а также параметр α=b/h0. Стойка может иметь различные закрепления в плоскостях xz и xy, коэффициенты приведения длины в этих плоскостях равны μxz и μyz соответственно. Требуется найти такие значения параметров α и β, чтобы критическая сила достигла максимума при постоянной массе стержня.
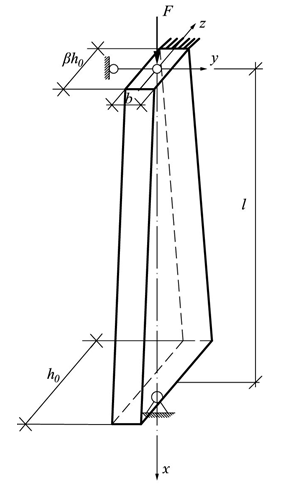
Рис. 1. Расчетная схема
Объем стержня можно вычислить по формуле:
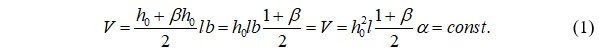
Выразим из (1) h0:
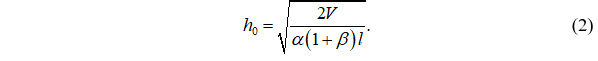
Для стержня постоянного сечения из упругого материала критическая сила определяется по известной формуле Эйлера:
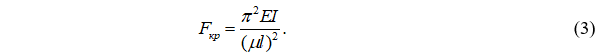
В действующих нормах проектирования деревянных конструкций для стержней с линейно меняющейся высотой поперечного сечения переменная жесткость учитывается коэффицентом kжN, который зависит от способа закрепления и параметра β. Уточнение нормативных формул коэффициента kжN нами было выполнено ранее. Расчетные формулы для коэффициента kжN представлены в таблице 1.
Табл. 1. Расчетные формулы коэффициента kжN
| закрепление | μ | плоскость xz | плоскость xy |
| шарнир-шарнир | 1 | 0.5116β2+0,5004β-0,0103 | -0,1305β2+0,7193β+0,4079 |
| шарнир-защемление | 0,7 | 0,515β2+0,5054β-0,0157 | -0,1731β2+0,793β+0,3783 |
| защемление-защемление | 0,5 | 0,5158β2+0,5037β-0,0172 | -0,2186β2+0,8624β+0,3499 |
| защемление-свободный край | 2 | -0,1158β2+1,0848β+0,025 | -0,1236β2+0,5089β+0,612 |
Критическая сила при потере устойчивости в плоскости xz может быть вычислена как:
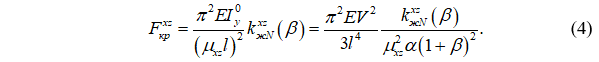
При потере устойчивости в плоскости xy формула критической силы принимает вид:
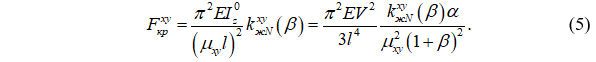
Целевую функцию представим в виде:
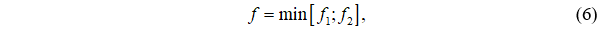
где 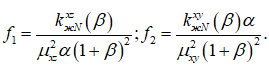
Требуется найти такие α и β, чтобы целевая функция принимала максимальное значение.
Решение задачи нелинейной оптимизации выполнялось в среде MATLAB с использованием пакета Optimization Toolbox для всех возможных сочетаний μxy = [0,5; 0,7; 1; 2] и μxz = [0,5; 0,7; 1; 2]. В качестве оптимизационного метода использовался алгоритм последовательного квадратичного программирования (SQP) [14-16]. Для β принимался диапазон возможных значений от 0,1 до 1, а для α — от 0,1 до 10.
Результаты и обсуждение
Полученные в результате оптимальные значения параметров α и β сведены в табл. 2.
Табл. 2. Оптимальные значения параметров α и β при различных закреплениях в двух плоскостях
|
μxz μxy |
0,5
|
0,7
|
1
|
2
|
| 0,5 | α=0,9817 β=0,9593 |
α=0,7021 β=0,9593 |
α=0,4877 β=0,9479 |
α=0,2162 β=0,5036 |
| 0,7 | α=1,3957 β=0,9905 |
α=0,9924 β=0,9801 |
α=0,6865 β=0,961 |
α=0,2998 β=0,4911 |
| 1 | α=2 β=1 |
α=1,4309 β=0,9955 |
α=0,991 β=0,9784 |
α=0,4235 β=0,4742 |
| 2 | α=3,4156 β=0,7719 |
α=2,4346 β=0,7671 |
α=1,6883 β=0,7556 |
α=0,731 β=0,3765 |
В табл. 2 серым выделены варианты, для которых оптимальный параметр β оказался близок к 1. Для этих вариантов использование переменного сечения неэффективно. Вообще говоря, для указанных вариантов βопт = 1, а αопт = μxy/μxz (из условия равноустойчивости в двух плоскостях), в чем можно убедиться, если построить поверхности f(α,β). Одна из таких поверхностей, соответствующая μxz=1 и μxy=0,7, показана на рис. 2. Оптимальная точка, найденная при помощи MATLAB, отмечена красным маркером. Отклонение β от 1 связано с тем, что касательная в отмеченной точке и при β=1 практически горизонтальна.

Рис. 2. Поверхность f(α, β) при μxz = 1 и μxy = 0,7
Из таблицы 2 видно, что использование переменного сечения с линейным изменением высоты по длине эффективно, только когда хотя бы в одной из плоскостей стержень закреплен по схеме «защемление-свободный край». На рисунке 3 приведена одна из таких поверхностей f(α,β), соответствующая случаю μxz=2 и μxy=0,5. При любых μxz и μxy поверхности f(α,β) имеют гребень, соответствующий равноустойчивому состоянию, на котором и находится оптимальная точка.
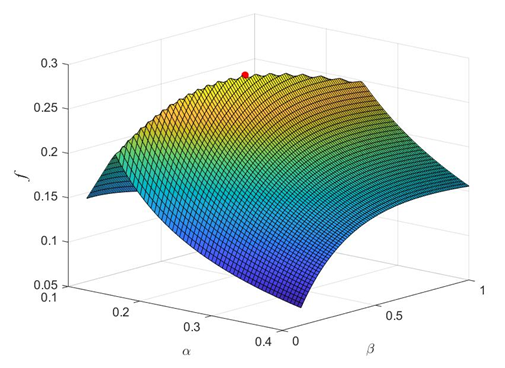
Рис. 3. Поверхность f(α, β) при μxz=2 и μxy=0,5
Положение этого гребня можно найти, если приравнять (4) и (5). В результате получим формулу:
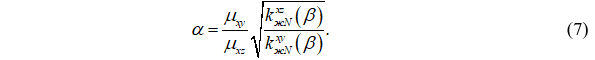
Подстановка (7) в (6) приведет к следующему выражению для целевой функции:
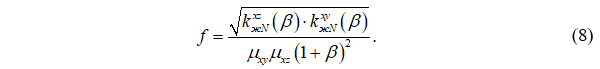
Продифференцируем (8) по β и приравняем к нулю:
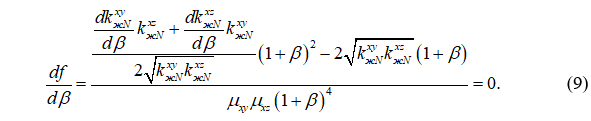
После упрощений задача поиска оптимального β сводится к уравнению:
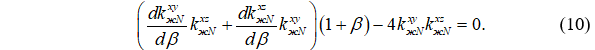
При использовании зависимостей, представленных в действующих нормах расчета деревянных конструкций, для некоторых вариантов закрепления решение уравнения (10) может быть получено аналитически. Так, при μxz=μxy=2:
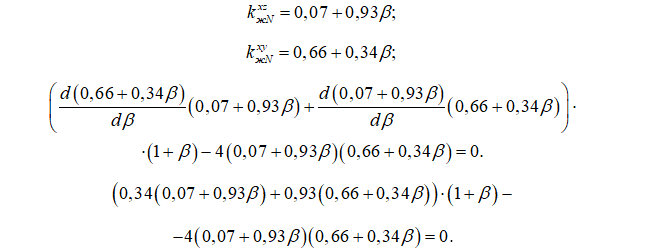
После упрощений имеем квадратное уравнение, которое в диапазоне β∈[0;1] имеет корень β=0,3071. Данное решение несколько отличается от результата, представленного в табл. 2, что объясняется различием нормативных и полученных нами формул коэффициентов kжN. При поиске минимума функции (6) в MATLAB с использованием нормативных формул было получено значение β=0,3072. По сравнению со стержнем постоянного сечения для оптимального стержня критическая нагрузка оказалась выше на 22%. Отметим, что в задаче Лагранжа максимально возможный прирост критической нагрузки составляет 33% [17-20].
Выводы
Аналитически и численно решена задачи оптимизации стержня прямоугольного поперечного сечения, высота которого меняется по линейному закону при возможной потере устойчивости в двух плоскостях. Для различных вариантов закрепления найдены оптимальные значения безразмерных геометрических параметров, обеспечивающие максимум критической нагрузки.
Установлено, что применение стержней с линейно меняющейся высотой целесообразно только в случае, когда по крайней мере в одной плоскости стержень закреплен по схеме «защемление-свободный край».
При использовании стержней переменной жесткости c линейно меняющейся высотой сечения прирост критической нагрузки может составить 22% по сравнению со стержнями постоянной жесткости.
1. Serov E. N., Labudin B. V. Kleyenyye derevyannyye konstruktsii: sostoyaniye i problemy razvitiya [Glued wooden structures: state and development problems] //Izvestiya vysshikh uchebnykh zavedeniy. Lesnoy zhurnal. - 2013. - No. 2 (332). - Pp. 137-146.
2. Pashkova M. E., Bazarova E. A., Andriyenko V. V. Bol'sheproletnyye derevyannyye konstruktsii [Long-span wooden structures] // Nauka i obrazovaniye: problemy, idei, innovatsii. - 2018. - No. 5. - Pp. 18-22.
3. Meshcheryakova A. A., Belokonev V. V. Kleyenyye derevyannyye konstruktsii i perspektivy ikh ispol'zovaniya [Glued wooden structures and prospects for their use] //Pokoleniye budushchego: vzglyad molodykh uchenykh. - 2016. - Pp. 45-48.
4. Nemirovskiy Yu. V., Boltayev A. I. Ratsional'noye proyektirovaniye sloistykh derevyannykh konstruktsiy [Rational design of layered wooden structures] // Problemy optimal'nogo proyektirovaniya sooruzheniy. - 2017. - Pp. 193-201.
5. Malykhina V. S., Ryazanova A. A. Analiz konstruktivnykh resheniy derevyannykh trekhsharnirnykh ram [Analysis of constructive solutions for wooden three-hinged frames] / V. S. Malykhina, A. A. //Vestnik Belgorodskogo gosudarstvennogo tekhnologicheskogo universiteta im. V. G. Shukhova. - 2018. - No. 6. - Pp. 33-38.
6. Karamisheva A. A., Yazyev S. B., Avakov A. A. Calculation of plane bending stability of beams with variable stiffness //Procedia Engineering. - 2016. - Vol. 150. - Pp. 1872-1877.
7. Seyranyan A. P. Zadacha Lagranzha o naivygodneyshem ochertanii kolonny [The Lagrange problem of the most advantageous outline of a column] // Uspekhi mekhaniki. - 2003. - No. 2. - Pp. 45 - 96.
8. Seyranian A. P., Privalova O. G. The Lagrange problem on an optimal column: old and new results // Structural and multidisciplinary optimization. - 2003. - Vol. 25. - No. 5. - Pp. 393-410.
9. Chepurnenko A. S., Yazyev B, M. Optimizatsiya formy poperechnogo secheniya szhatykh sterzhney iz usloviya ustoychivosti [Optimization of the cross-sectional shape of compressed rods from the stability condition] // Nauchnoye obozreniye. - 2012. - № 6. - Pp. 202-204.
10. Manevich A. I., Raksha S. V. Optimal'nyye tsentral'no szhatyye sterzhni otkrytogo profilya [Optimal centrally compressed open profile rods] // Theoretical Foundations of Civil Engineering - VÍÍÍ: Ed. by W. Szczsniak, OW PW Warsaw. - 2000. - Pp. 484-489.
11. Leont'yevskaya E. D., Tukhfatullin B. A., Puteyeva L. E. Optimizatsiya formy poperechnogo secheniya sterzhney pri ogranicheniyakh po ustoychivosti i prochnosti na szhatiye [Optimization of the shape of the cross-section of rods under constraints on stability and compressive strength] // Izbrannyye doklady 62-y universitetskoy nauchno-tekhnicheskoy konferentsii studentov i molodykh uchenykh. - 2016. - Pp. 41-44.
12. Lyakhovich L. S. Osobyye svoystva form poteri ustoychivosti sterzhney minimal'noy materialoyemkosti pri ogranichenii velichiny kriticheskoy nagruzki dlya sluchayev lineynoy zavisimosti momentov inertsii secheniy i funktsii tseli ot var'iruyemogo parametra [Special properties of buckling forms of rods with minimum material consumption when limiting the critical load value for cases of linear dependence of the moments of inertia of sections and the target function on a variable parameter] //Vestnik Tomskogo gosudarstvennogo arkhitekturno-stroitel'nogo universiteta. - 2011. - No. 4. - Pp. 106-112.
13. Fedorov I. M., Temis Yu. M. Optimizatsiya formy sterzhney pri nekonservativnom nagruzhenii po kriteriyu poteri ustoychivosti [Optimization of the shape of rods under non-conservative loading according to the criterion of buckling] // Problemy prochnosti i plastichnosti. - 2007. - No. 69. - Pp. 24-37.
14. Gill P. E., Murray W., Saunders M. A. SNOPT: An SQP algorithm for large-scale constrained optimization //SIAM review. - 2005. - Vol. 47. - No. 1. - Pp. 99-131.
15. Biggs M.C. Constrained Minimization Using Recursive Quadratic Programming // Towards Global Optimization (L.C.W. Dixon and G.P. Szergo, eds.), North-Holland. - 1975. - Pp. 341-349.
16. Nocedal J., Wright S. J. Numerical Optimization, Second Edition. Springer Series in Operations Research, Springer Verlag, 2006. - 664 p.
17. Antonenko E. V., Khloptseva N. S. Effektivnost' szhatykh sterzhney [Efficiency of compressed rods] //Matematika. Mekhanika. - 2007. - No. 9. -Pp. 124-126.
18. Yegorov Yu. V. O zadache Lagranzha ob optimal'noy forme kolonny [On the Lagrange problem of the optimal form of a column] // Doklady Akademii nauk. - Federal'noye gosudarstvennoye byudzhetnoye uchrezhdeniye "Rossiyskaya akademiya nauk", 2003. - Vol. 392. - No. 5. - Pp. 598-602.
19. Yegorov Yu. V., Kondrat'yev V. A. Ob optimal'noy forme kolonny [On the optimal form of a column] //Doklady Akademii nauk. - Rossiyskaya akademiya nauk, 1996. - Vol. 350. - No. 6. - Pp. 727-729.
20. Goncharov V. Yu., Muravey L. A. Nekotoryye ostsillyatsionnyye svoystva resheniy v zadache o potere ustoychivosti kolonny [Some oscillatory properties of solutions in the problem of column buckling] //Differentsial'nyye uravneniya, matematicheskoye modelirovaniye i vychislitel'nyye algoritmy. - 2021. - Pp. 90-92.


















