from 01.01.1977 to 01.01.2023
Rostov-on-Don, Rostov-on-Don, Russian Federation
Rostov-on-Don, Rostov-on-Don, Russian Federation
The dynamic impact of moving vehicles can cause effects leading to landslide processes in slopes. Even insignificant displacements and speeds lead to a relative displacement of the layers. In this case, the physical and mechanical parameters of the soils that make up the slope can change significantly. For example, the decrease in adhesion C may be analogous to the decrease in the force of static friction by the transition to sliding friction. This is due to the fact that the mutual movement leads to slippage of small soil fragments relative to each other. The influence of vehicles on possible landslide processes increases with an obvious tendency to increase the speed and mass of the rolling stock. This, as well as the complex geological structure of the slopes and the need to take into account the reinforcing structures, leads to the need to build refined mechanical and mathematical models for the joint operation of road structures, the slope and the reinforcing structures in a dynamic formulation. The creation of a refined model of the slope geometry, the highway and the slope reinforcement structures are today solved mainly by the finite element method (FEM). The problem of constructing a numerical solution of such problems based on direct methods of integrating the equations of motion is topical. In this case, it is necessary to take into account the change in the distribution of masses when moving vehicles along the road at different speeds. In any of works of the author [1-6], an explicit absolutely stable scheme for integrating the equations of motion of the FEM was used to solve this problem. This article considers testing of the method by comparing numerical solutions with known ones for problems that are simpler in terms of topological structure. Namely, the comparison of the method with the solutions of the classical problem "movement of a massive load along a massive beam" was carried out. V.V. Bolotin's solution [7-9] was adopted as a "reference" one. Numerical solutions showed a high degree of convergence of results by the proposed and "reference" methods.
finite element method, variational equation, equation of motion, variable mass, dynamics, static, stability of numerical methods, explicit direct integration schemes, implicit direct integration schemes, absolutely stable schemes
Введение
Рост скорости и массы подвижного состава неуклонно возрастает последние десятилетия. В связи с этим возрастает роль динамического расчета инженерных конструкций на действие подвижных нагрузок. К таким расчетам относятся задачи нахождения напряженно-деформированного состояния (НДС) системы и его максимальных параметров (максимальных напряжений, перемещений, скоростей и ускорений), задачи определения несущей способности и устойчивости конструкции под воздействием подвижных нагрузок.
Исследования, посвященные учету динамических эффектов от движения нагрузки, начались более 150 лет назад – после обрушения Честерского моста (Англия, май 1847 г). Работы, посвященные этой проблеме, выполнялись известными учеными: Брессом, Гогенемзером, Прагером, С. А. Бернштейном, А. Н. Крыловым, С. П. Тимошенко, Я. Г. Пановко и И. И. Губановой, А. П. Филипповым и многими другими.
По степени учета инертности конструкции и нагрузки эти исследования разделялись на четыре класса:
- без учета инерционных свойств конструкции и нагрузки,
- учет только инерционных свойств конструкции,
- безмассовая конструкция и массивная нагрузка,
- учитывается как масса конструкции, так и нагрузки.
Очевидно, что последняя постановка наиболее общая, т.к. первые три могут рассматриваться как частные случаи решения в постановке учета масс конструкции и груза.
Прямое интегрирование уравнений движения в форме метода конечных элементов
При движении транспорта по полотну автомобильной дороги на части объема V1 инерционные свойства системы остаются постоянными, но на поверхности полотна происходит постоянное перераспределение масс системы за счет перемещающихся со скоростью vt массивных объектов.
Согласно [11-13], на основе уравнения Мещерского, уравнения динамической теории упругости с переменной массой записаны в (1):
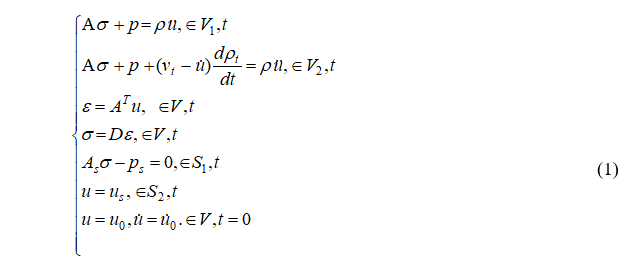
Вариационное уравнение типа Лагранжа в свертках для системы с переменной массой (2) получено на основе известного подхода Гэртина [11].
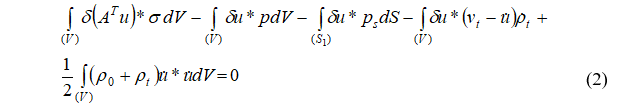
Для пространственной области уравнения движения в форме метода конечных элементов (3) строится традиционно.
В работе используется явная абсолютно устойчивая схема прямого интегрирования уравнений движения с переменной массой (4), которая была впервые получена в работах Л.Н.Панасюка и В.П.Матуа [7, 10-11]:
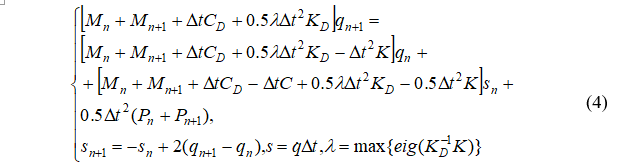
Приведенная явная схема является абсолютно устойчивой в смысле критерия Дж.Неймана [4]. Доказательство факта абсолютной устойчивости базируется на разложении (4) по собственным формам матрицы KD-1K. Доказана ортогональность собственных векторов разложения. В результате чего систему (4) можно представить в «расщепленной» форме (5) [5-6]:
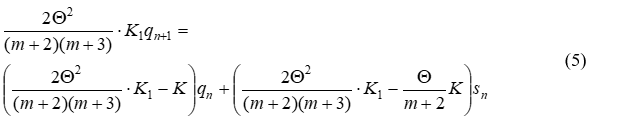
Абсолютная устойчивость обеспечена при =0.5(m+3)λ. Здесь ƛ – максимальное собственное число матрицы (KD)-1K [43, 48-50].
«Эталонное» решение задачи
Для тестирования схемы (4) рассмотрено известное решение В.В. Болотина [1-3, 8]. Им обобщена предложенная Инглисом система дифференциальных уравнений движения по балке произвольной системы масс в любой комбинации нагрузок. Инерционные свойства подвижной нагрузки были построены в форме (6):
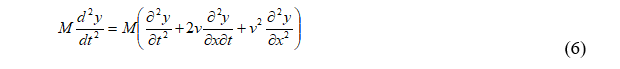
Во многих исследованиях задач динамики балок с подвижными массивными нагрузками результаты В. В. Болотина принимаются за эталон. Уравнение вида (6) называют уравнением Инглиса — Болотина. Аналитическое решение (6) не найдено. Известные решения получены численно. Наиболее часто применяемым является метод Бубнова-Галеркина. При удержании одного симметричного члена разложения (7) априори задается симметричная изогнутая ось балки в любой момент времени, что не соответствует истинной картине решения. Для уточнения решения В.В.Болотина в работе рассмотрена аппроксимация со вторым кососимметричным слагаемым (8).
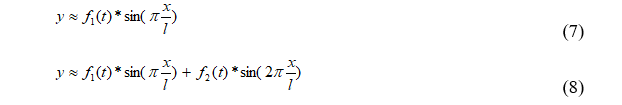
Использование (7) и (8) порождает системы обыкновенных дифференциальных уравнений (9) и (10) относительно аргумента времени t:
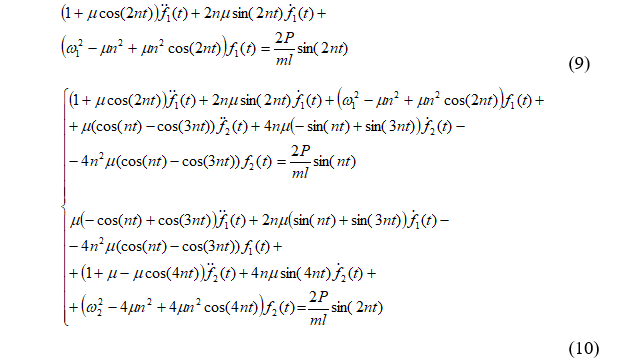
В (9)-(10) использованы обозначения:
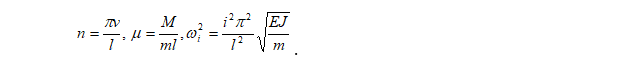
Используя замену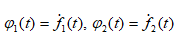 
, уравнения (9) и (10) сводятся к системе из двух и четырех уравнений первого порядка соответственно (здесь не приведены).
Численное решение последних уравнений используется для получения «эталонных» численных решений методом Рунге-Кутта 6 порядка, реализация выполнена с использованием функций комплекса Scilab.
При реализации предлагаемого МКЭ подхода (4) ось балки разбивалась на плоские балочные конечные элементы с четырьмя степенями свободы (продольными деформациями пренебрегали). Ось балки разбита на 100 конечных элементов. Локальные матрицы балочных элементов (11) построены традиционно. Тестируемое решение строилось в комплексе Scilab.
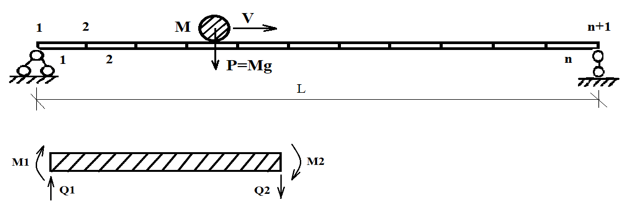
Рисунок 1. МКЭ модель балки и степени свободы балочного элемента
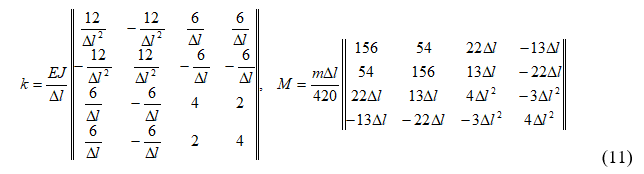
Выборка результаты тестовых расчетов
В расчетах варьировались отношение массы груза к массе балки в сегменте [0.05…0.5] и отношение скорости груза к «критической» в таком же сегменте.
На рис. 2-7 показана выборка некоторых результатов сравнительных расчетов. Графически результаты представлены в виде четырех графиков. Три графика отражают колебания точек балки на расстоянии 0.25, 0.50 и 0.75 от длины пролета. На четвертом графике показана деформированная ось балки в различные моменты времени. В первых трех графиках время сопоставлено с положением груза на балке приведенной единичной длины. Т.е., эти три графика можно рассматривать как динамические линии влияния перемещений различных точек балки единичной длины. Графики даны на сегменте [0…1.4] от длины пролета, что соответствует движению груза по балке и после схода с нее. На сегменте [1… 1.4] наблюдаем свободные колебания, возникающие после «схода» груза с конструкции.
Влияние удержания одного или двух членов аппроксимации решения методом Бубнова-Галеркина отчетливо прослеживается для сечений балки, расположенных на первой и последней четверти пролета. Для них более приближенное решение при удержании одного члена аппроксимации (зеленая ветвь) имеет большую погрешность, чем для практически совпадающих решений согласно (4) и (10). Однако для центрального сечения балки все три решения практически совпадают. Также совпадают все три решения в области свободных колебаний сечений после схода груза с балки.
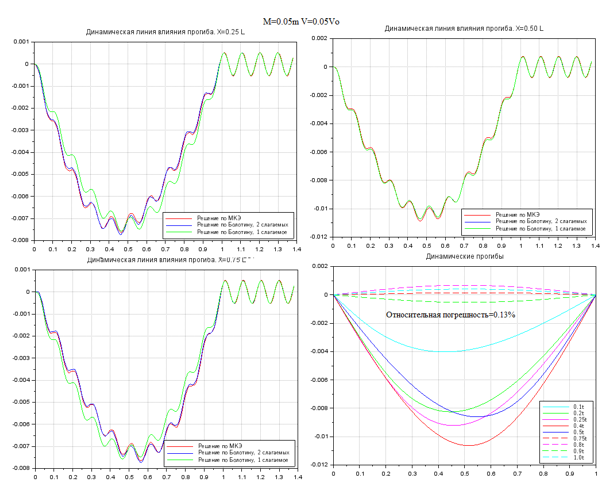
Рисунок 2. Колебания при M=0.05m, V=0.05V0
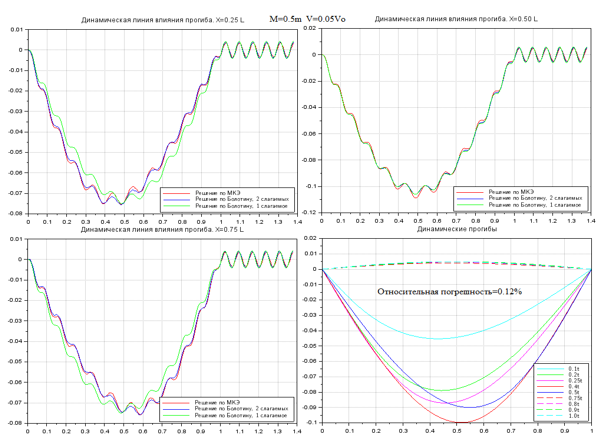
Рисунок 3. Колебания при M=0.5m, V=0.05V0
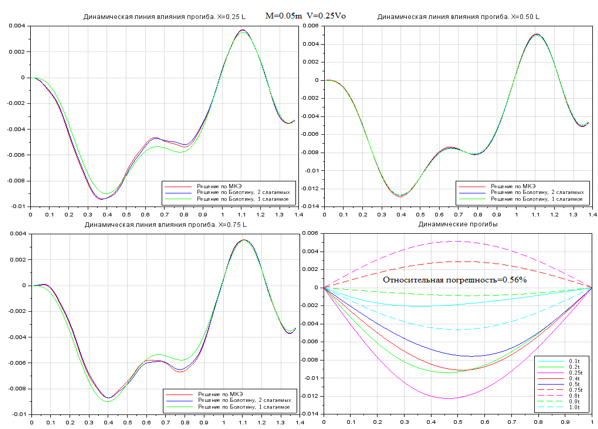
Рисунок 4. Колебания при M=0.05m, V=0.25V0
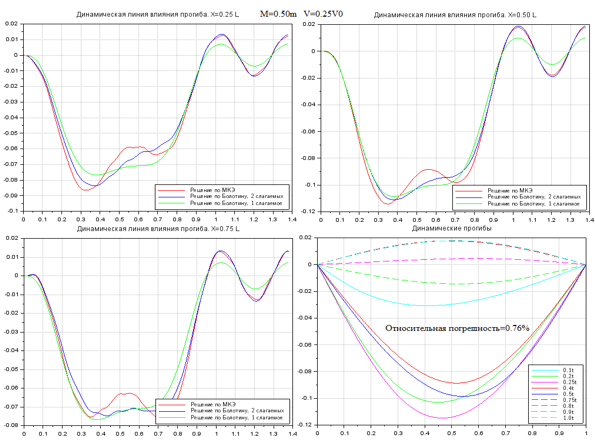
Рисунок 5. Колебания при M=0.50m, V=0.25V0
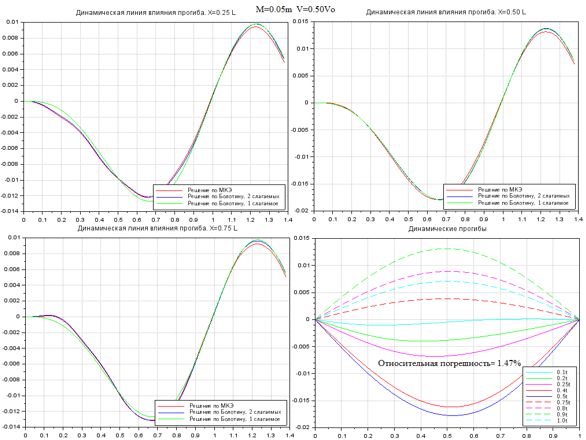
Рисунок 6. Колебания при M=0.05m, V=0.50V0
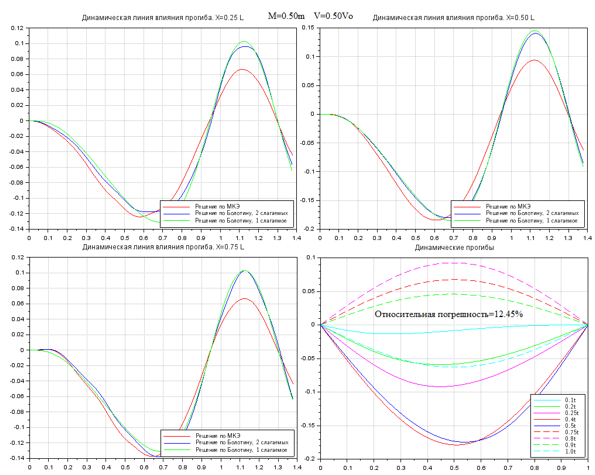
Рисунок 7. Колебания при M=0.50m, V=0.50V0
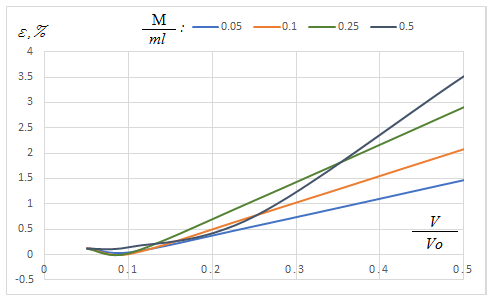
Рисунок 8. Среднеквадратичная погрешность, (%)
Выводы по тестовой задаче
Анализ результатов показывает высокую степень совпадения результатов, полученных по тестируемой схеме (4) с известными «эталонными» решениями (9)-(10).
Отметим, что решения (4) в большей части области совпадает с уточненным решением уравнений В.В. Болотина (10). Различия между результатами по (9) и по (10) указывают на необходимость учитывать кососимметричные слагаемые в аппроксимации по пространственной оси в методе Бубнова-Галеркина.
Относительная погрешность для большей части результатов между эталонным (10) и тестируемым (4) имеет порядок 0.1%.
Максимальная погрешность достигается при высоких скоростях движения, равных половине критической скорости, но не превышает 3-3.5%.
Анализ погрешности решения позволяет сделать вывод, что явную абсолютно устойчивую схему интегрирования уравнений движения в форме МКЭ (4) можно применять в реальных задачах со сложной геометрией и распределением физико-механических параметров расчетной пространственной области.
Модельный пример расчета движения автомобилей по двухполосной дороге, расположенной на склоне
По изложенной методике выполнено моделирование движения автомобилей по автомобильной дороге, расположенной на склоне. В расчете варьировались типы и скорости движения автомобилей, полоса движения (первая или вторая), расположение автодороги от края склона (0,25; 0,5; 0,75; 1,0 метров). Конечно-элементная модель неоднородного склона (по поперечному сечению) приведена на рис. 9. В данной реализации программного комплекса в графическом редакторе формировалась конечно-элементная модель поперечника склона. Системы разрешающих уравнений (4) для пространственной задачи автоматически формировались методом экструзии из плоской конечно-элементной модели поперечника [14-15]. Расчет выполнялся в пространственной постановке. Конечные элементы – треугольные призмы, с тремя линейными степенями свободы в узлах – автоматически формируются из плоских треугольных элементов.
Результаты приведены для некоторых типов автомобилей (двухосный грузовой автомобиль, четырехосный грузовой автомобиль, трехосный седельный автопоезд). Параметры автомобилей приняты согласно действующим нормам проектирования автомобильных дорог.
Основные данные расчета: ширина одной полосы автомобильной дороги 3.5м. Состав дорожной конструкции: верхний слой 50мм – мелкозернистый асфальтобетон ЩМА-15, второй слой 100мм – крупнозернистый пористый асфальтобетон, третий слой 300мм – гравийно-песчаная смесь С1. Параметры автомобилей показаны на рис. 3.1.
Размер сетки конечных элементов варьировался от 0,1м в окрестности автомобильной дороги и угловых точек до 0,5 – 0,6 м в удаленных зонах. Общее число узлов сетки конечных элементов 427 тысяч, что соответствует порядку матрицы жесткости 1281000. Матрица масс принята несогласованной, точечные массы консолидированы в узлах. Поэтому матрица масс диагональная. Для устранения эффекта отражения волн от границ области в окрестности границ введено два фиктивных слоя с повышенными коэффициентами демпфирования (0,5 и 0,7 от критического). Этот известный прием обеспечивает затухание прямой и отраженных волн в окрестности границ расчетной области.
Рассматривался фрагмент автодороги длиной 30м. Автомобили с разной скоростью двигались по дороге. Шаг интегрирования принят 0,001с.
В результатах фиксировались данные по среднему сечению (на расстоянии 15м от начала автомобильной дороги).
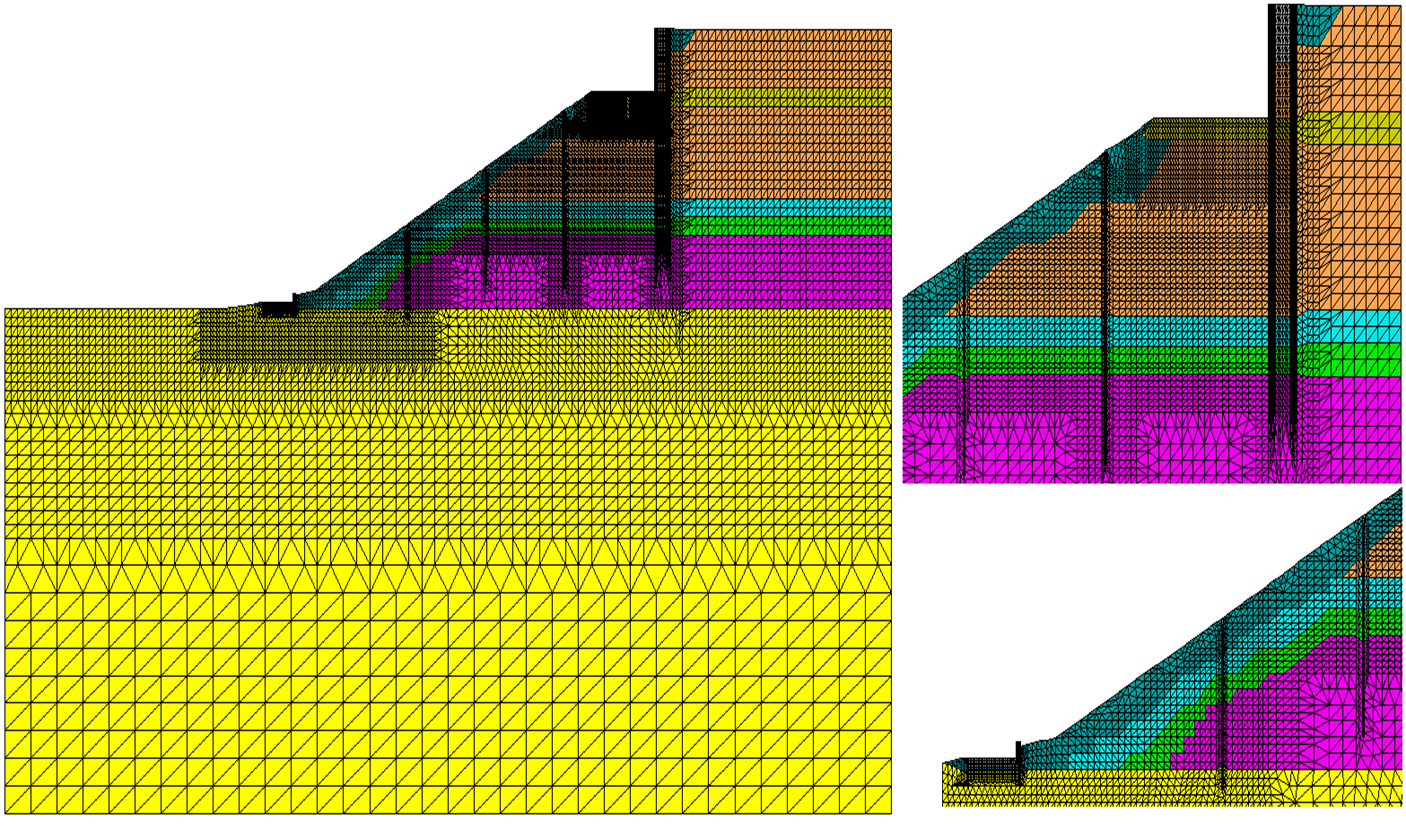
Рис. 9. Конечно-элементная модель поперечного сечения усиленного склона
На рисунках 10-11 показаны примеры графиков колебаний ряда точек поперечного сечения на расстоянии 15м от начала дороги. На каждом рисунке в левом ряду графиков показаны динамические перемещения точек при движении автомобиля по полосе 1 (ближней к краю откоса), в правом ряду – при движении по полосе 2 (дальней от края откоса).
В результатах очевидно влияние скорости движения на динамическую реакцию конструкции. Хотя для каждого типа автомобилей неизменна нагрузка, передаваемая со стороны колес на поверхность дороги, также неизменны расстояния между колесными осями и расположением колес на оси, очевидно отличие в графиках колебаний при движении с разной скоростью. Статическая постановка не позволяет учесть этот эффект. При увеличении скорости нарастают максимальные перемещения, а также увеличивается «выпор» — подъем в процессе колебаний отдельных точек дорожной конструкции. Затем, при увеличении скорости, перемещения начинают снижаться. Также величины перемещений зависят от полосы движения. При движении автомобиля по дальней от края откоса полосе перемещения снижаются – рис. 12.
На каждом графике рис. 10-11 показаны колебания по 15 точкам поперечного сечения. Отчетливо просматривается, что в колебательный процесс входят не только точки, расположенные по колее движения автомобиля, но и точки, расположенные на свободных от воздействия полосах дороги.
Прослеживается воздействие колес передней и задних осей. На рис. 10 точки автомобильной дороги «не успели» вернуться в исходное состояние перед воздействием задних колес. На рис. 11 колеса задней оси действуют на сечение, получившее противоположное перемещение (вверх).
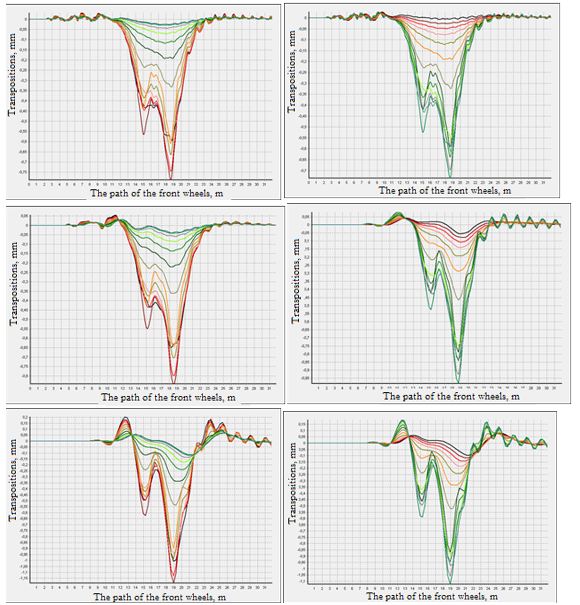
Рисунок 10. Двухосный грузовой автомобиль. Полосы 1- 2. A= 0.25м. v=30, 60, 90, 110км/ч
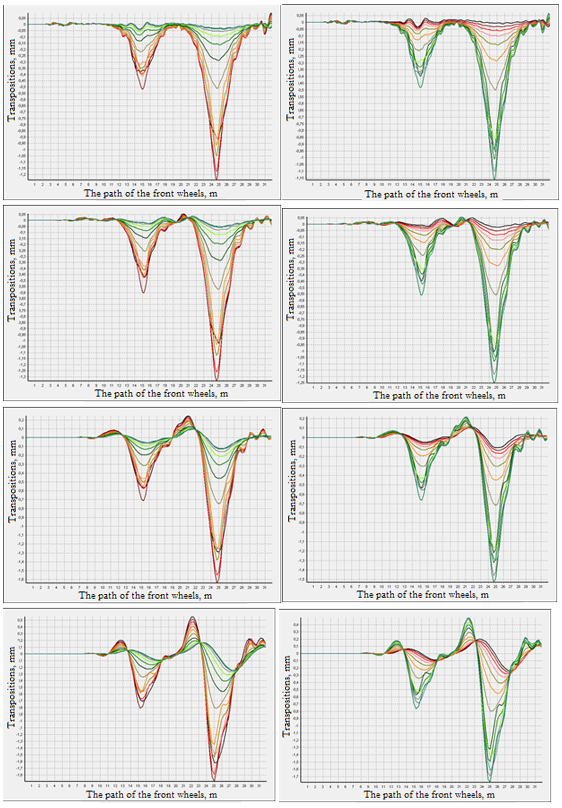
Рисунок 11. Трехосный седельный автопоезд. Полосы 1 и 2. A= 0,25м. v=30, 60, 90, 110км/ч
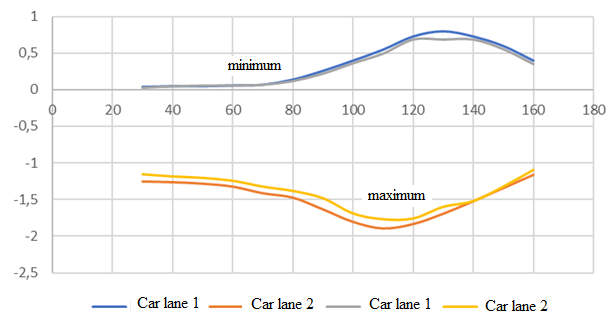
Рисунок 12. Максимальные перемещения (прогиб и выпор) при движении
Выводы
Основной вывод состоит в том, что моделирование работы склона в динамической постановке позволяет получить эффекты решения, которые нельзя моделировать в статической постановке.
Приведенный пример показывает необходимость использования динамического подхода при моделировании работы оползневых склонов.
Построенные уравнения позволяют учитывать такие параметры, как:
- инерционность подвижного состава и дорожной конструкции;
- скорость движения отдельных транспортных средств;
- предполагаемую интенсивность грузопотока в различные моменты времени (года и суток);
- влияние сезонно-климатических факторов (влажность грунта и температура асфальтобетона), изменение температуры в течение суток;
- неоднородность конструкций дорожной одежды и грунтового массива в плане и по глубине.
1. Bolotin V.V. On the impact of a moving load on bridges / - Proceedings of MYIT, vol. 74, 1950.
2. Bolotin V.V. On the dynamic calculation of railway bridges, taking into account the mass of the moving load. - Proceedings of MIIT, vol. 76, 1952.
3. Bolotin V.V. The problem of vibrations of bridges under the action of a moving load / - Izv. USSR Academy of Sciences, OTN, mech-ka and mechanical engineering, No. 4, 1961.
4. Vasilkov, G. V., Panasiuk, L. N. On the solution of physically nonlinear problems of the dynamics of structures by direct methods. - Izvestiya Universities. Construction and architecture, 1988, N 5, - S. 39-43.
5. G. I. Marchuk, Splitting methods. - M.: Nauka, 1988. - S. 28-40.
6. Marchuk, G. I. Mathematical modeling in the environmental problem. - M.: Nauka, 1982. - 341 p.
7. Matua V.P., Panasiuk L.N., Chirva D.V., Mironchuk S.A., Sizonnets S.V., Isaev E.N. - Modern methods for predicting residual deformations in road structures (scientific monograph). - Rostov n/a. : DSTU, 2019
8. Morgaevsky A.B. Investigation of beam oscillations under the action of a moving load in the form of a half-strip at high speeds Issled. on the theory of structures", issue 13, M. 1964, pp. 105-120
9. Panasiuk L.N., Tyurina V.S., Chubka Yu. Sh., Poshev A.U-B. Simulation of the operation of landslide slopes under dynamic impact // Engineering Bulletin of the Don [Electronic resource]: electron. scientific - innovative. magazine 2018. №2.
10. 10. Panasiuk L.N., Matua V.P. Mechanical and mathematical model for predicting the accumulation of residual deformations in the elements of road structures in real conditions of their operation, - Improving the quality and durability of road structures: materials of the International. scientific-practical. conf., May 24-25, 2018 / Don. state tech. un-t. - Rostov n / a.: DSTU, 2018. - P. 27-34
11. Panasiuk, LN On the construction of stable schemes for direct integration of nonlinear equations of motion. Rostov n / a, RGAS. - Dep. in VINITI N 1099-B94.-8p.
12. Panasiuk, LN On the construction of explicit unconditionally stable schemes for direct integration of the problem of structure dynamics. Izvestiya vuzov. Construction, 1995.
13. Panasiuk L.N., Kravchenko G.M., Matua V.P. Numerical method for solving the problems of the building structures dynamics with a mobile massive load// Materials Science Forum ISSN: 1662-9752, Vol. 931 MSF, pp 72-77, 2018 Trans Tech Publications, Switzerland
14. L Panasiuk, V Turina, D Stupina. The supported landslide slopes' operation simulation //IOP Conference Series: Materials Science and Engineering. Construction mechanics, building materials and theory of structures, civil and industrial engineering: Volume 698, Issue 2.
15. L Panasiuk, V Turina. The stress-strain state simulation of slopes with dynamic loads //IOP Conference Series: Materials Science and Engineering. Construction mechanics, building materials and theory of structures, civil and industrial engineering: Volume 698, Issue 2.
