Novocherkassk, Rostov-on-Don, Russian Federation
graduate student
Novocherkassk, Rostov-on-Don, Russian Federation
employee
Novocherkassk, Rostov-on-Don, Russian Federation
from 01.01.2019 until now
Platov South-Russian State Polytechnic University (NPI) (Obscheinzhenernye discipliny, professor)
from 01.01.1980 to 01.01.2019
Moskva, Moscow, Russian Federation
BBK 308 Монтаж, эксплуатация, ремонт машин и промышленного оборудования
The paper studies a two-dimensional water flow that flows from a non-pressure rectangular or round pipe into a wide horizontal channel. To simplify the problem, the real three-dimensional flow is modeled as a two-dimensional zone by eliminating the velocities and accelerations of liquid particles in the direction perpendicular to the flow zone. To describe the law of motion of the water flow, the equations of L. Euler for the ideal fluid are used, taking into account the continuity equations and the Bernoulli equation. Models of two-dimensional flow in the spreading zone with the degree of adequacy sufficient for practice describe the movement of water flows arising in the lower races of road drainage systems, systems of Liman irrigation, small bridges, channels of volley of water, various culverts and water-crossing facilities. The obtained dependences of the velocity distribution, depth and water flow geometry give an accuracy exceeding that known by the previously used methods both by the velocity values and by the geometry of the boundary current lines.
hydraulic structures, two-dimensional open water flow, rectangular and circular cross-section pipes, wide horizontal diverting channel, Euler equations, calculation of velocities and boundary current lines
Целью настоящей работы является обзор различного вида уравнений движения двухмерного в плане открытого водного потока и решение некоторых практических задач с помощью этих уравнений.
Основные допущения и исходные физические предпосылки двухмерных в плане водных потоков следующие:
а) вертикальные (или нормальные к выбранной координатной плоскости) составляющие местных осреднённых скоростей и ускорений малы;
б) векторы скоростей жидких частиц, расположенных на одной вертикали, лежат в одной плоскости;
в) распределение скоростей на любой вертикали практически равномерное.
Можно выделить достаточно широкий класс потоков, параметры которых отвечают этим допущениям.
Такие потоки называют двухмерными в плане, отражая то, что для их описания достаточно двух геометрических координат x, y.
В широкой математической и технической литературе известно, что для постановки и решения различных прикладных задач по течению водных потоков необходимо пользоваться уравнениями движения, описывающими процесс течения жидкости, и знать начальные и граничные условия.
Так сложилось исторически, что основоположники теории двухмерных в плане водных потоков исходили из динамических уравнений движения идеального двухмерного открытого водного потока в форме Л. Эйлера (уравнений движения идеальной жидкости), дополненных слагаемыми, учитывающими силы сопротивления жидкости:
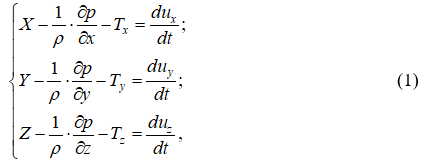
где X, Y, Z – компоненты объёмных сил; Tx, Ty, Tz – компоненты сил сопротивления, отнесённых к единице массы жидкости; r – плотность жидкости; p – местное давление; ux, uy, uz – компоненты вектора местной скорости.
Для установившегося потока при вертикальном направлении оси z и действии в жидкости единственной объёмной силы (силы тяжести) система (1) приобретает вид:
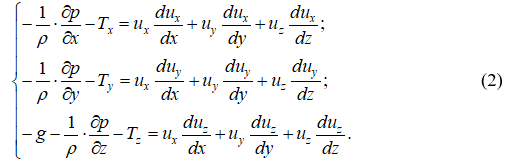
В силу посылки о малости вертикальных составляющих скоростей и ускорений все инерционные составляющие, содержащие uz и её производные, могут быть отброшены.
Тогда третье уравнение системы (2) примет вид:
где g – ускорение силы тяжести.
Интегрируя уравнение (3), получим:
где 
– произвольная функция.
С учётом того, что на свободной поверхности 
, приходим к гидростатическому закону распределения давлений на вертикали:
Обозначив через z0 координату дна водотока, получим:
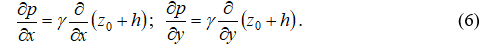
Тогда систему динамических уравнений движения потока можно записать в виде:
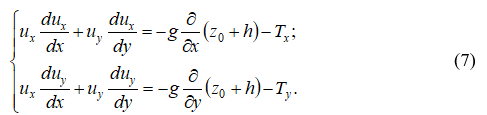
Дополнив эту систему уравнений уравнением неразрывности потока:
получим следующую систему течения потока в виде:
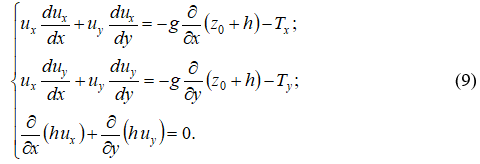
В частном случае, когда дно водовода горизонтальное, система (9) приобретает вид:
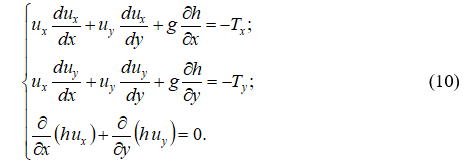
В ряде потоков, встречающихся в практике (выход потока из отверстия в расширение, вход потока в сужение, течение на виражах, на коротких участках) силами сопротивления потоку можно пренебречь, особенно в бурных высокоскоростных потоках, для которых силы инерции значительно превосходят силы тяжести, и система уравнений (10) приобретает вид:
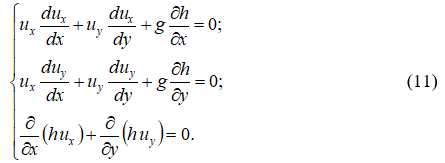
Система дифференциальных уравнений в частных производных (11) описывает течение двухмерных в плане открытых стационарных потоков в горизонтальном водоводе без учёта сил сопротивления потоку.
Эта система является системой существенно нелинейных уравнений, замкнутой относительно неизвестных функций:
С использованием системы (11) решаются различные задачи по течению двухмерных в плане водных потоков, как прямые, так и обратные.
Если ввести дополнительное условие потенциальности потока:
где W – вихрь для двухмерного потока, то существует потенциальная функция 
Система уравнений (11) в этом случае сводится к виду:
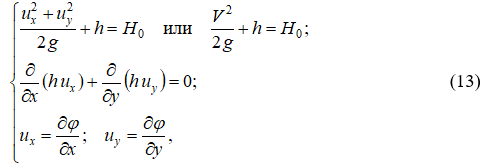
где H0 – постоянная для всего потока, определяемая по параметрам потока V0, h0 в некоторой характерной точке потока.
Первое конечное уравнение в системе (13) имеет название интеграла Д. Бернулли для двухмерных в плане водных потоков.
Система уравнений (13) сводится к одному уравнению второго порядка в частных производных относительно потенциальной функции 
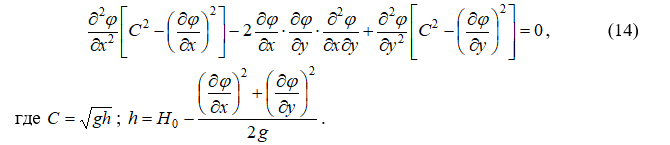
Это уравнение по внешнему виду совпадает с уравнением для потенциала скорости плоского безвихревого газа, причём скорости звука соответствует волновая скорость C.
Из уравнения неразрывности потока (8) следует существование функции тока, удовлетворяющей условиям:
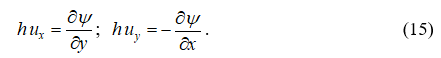
Поэтому систему (11) можно свести также к одному дифференциальному уравнению второго порядка в частных производных относительно функции тока 
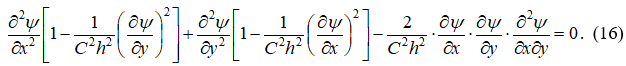
Уравнения (14), (16) служат исходными для разработки методов расчёта двухмерных в плане бурных потоков.
Для бурных потоков эти уравнения относятся к гиперболическому типу и для их исследования может быть использован метод характеристик.
К сожалению, метод расчёта потоков с использованием характеристик является численно-графо-аналитическим и даёт не всегда достаточную адекватность для практического пользования результатами модели.
Гораздо более точные результаты дают аналитические модели, изложенные в монографиях.
Следует заметить, что модель двухмерного в плане потенциального бурного потока, несмотря на значительную степень идеализации, имеет важное теоретическое и практическое значение.
Теоретическое значение заключается в том, что, исследуя простую модель, можно выявить характерные свойства потока и использовать их в более сложных моделях.
Практическое использование результатов модели потенциального течения в горизонтальном русле возможно в случаях, когда роль сил сопротивления относительно невелика (местные сужения, расширения или изгибы русла). В таких потоках основное формирующее влияние на параметры потока оказывает его инерционность и, если протяжённость потока незначительна, влиянием сил сопротивления можно пренебречь.
Аналитические методы решения различных задач по течению двухмерных в плане потенциальных потоков применяются:
а) в случае упрощений для потенциальной модели:
- уравнения движения простой центрированной волны;
- радиальный поток (безнапорный потенциальный источник).
б) при использовании вспомогательной плоскости годографа скорости.
Согласно уравнениям (13), (15) систему движений двухмерных в плане потенциальных водных потоков можно записать в виде:
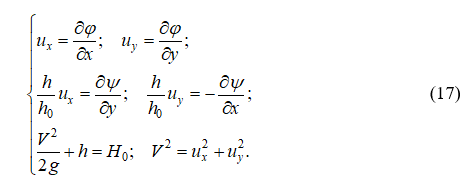
Переходом в плоскость годографа скорости 
, в которой независимыми координатами являются 
(квадрат скоростного коэффициента) и угол q, характеризующий направление вектора скорости, уравнения (17) трансформируются к виду:
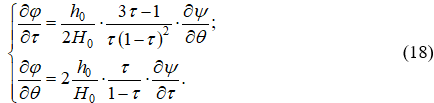
Формулы для определения глубин и скоростей при заданном параметре t имеют вид:
Зависимыми параметрами, неизвестными функциями в системе (18) являются 
– потенциальная функция; 
– функция тока, при этом для бурных потоков
Формулы (19) следуют из интеграла Бернулли и из выражения для параметра t.
Система уравнений (18) является уже линейной системой дифференциальных уравнений в частных производных в отличие от системы (11). Эта система сводится к решению следующего уравнения математической физики:
Это уравнение рядом замен приводится к гипергеометрическому уравнению с действительными коэффициентами, решения которого известны. Авторы работы на базе аналитических решений системы (18) развили метод, который может использоваться при решении различных задач по течению потенциальных двухмерных в плане открытых стационарных водных потоков.
Сначала решается граничная задача в плоскости годографа скорости.
Далее переход в физическую плоскость течения потока осуществляется использованием дифференциальной связью между планом течения потока и плоскостью годографа скорости:
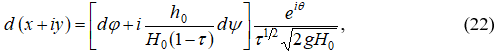
где 
– мнимая единица; x, y – координаты жидкой частицы потока в плане его течения; t, q – независимые координаты в плоскости годографа скорости; 
– потенциальная функция; 
– функция тока.
В работах авторы разработали детальную технологию решения задач по течению двухмерных в плане потенциальных потоков.
В работах приведены уравнения характеристик в плоскости годографа скорости; этот результат и аналогия внешнего вида уравнений совершенного газа и потенциального двухмерного в плане водного потока позволили авторам работ использовать преобразование С.А. Чаплыгина для получения системы (18) и разделения решения граничной задачи на два этапа:
1-й – решение задачи в плоскости годографа скорости;
2-й – получение алгоритма определения параметров потока в физической плоскости течения (в плане течения) с помощью интегрирования связи (22) при найденных на 1-м этапе функциях 
Далее приведём один из методов определения сил сопротивления потоку при использовании системы (9).
Для потоков, в которых нельзя пренебречь силами сопротивления потоку со стороны водовода, учёт сил сопротивления можно по предложению авторов в осуществить сведением поверхностных сил к некоторым эквивалентным объёмным.
Если t – касательное напряжение в основании элементарного цилиндрического объёма, то сила трения по дну равна 
. Направление вектора этой силы противоположно направлению вектора скорости 
Тогда абсолютные величины этой силы, отнесённые к единице массы выделенного объёма, выразятся формулами:
Или, вводя коэффициент гидравлического трения:
компоненты сил сопротивления переписываются в виде:
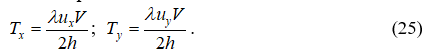
Как известно из, коэффициент Шези C связан с коэффициентом гидравлического трения соотношением:
причём 
; показатель y определяется конкретным законом сопротивления, приводимым в известной литературе по гидравлике; n – коэффициент шероховатости стенок водовода.
Для разрывных течений по параметрам потока пользуются двухмерными уравнениями планового потока (Сен-Венана), записанными в виде:
S – произвольная поверхность в пространстве (x, y, t), ограничивающая некоторый объём R в этом же пространстве; h – глубина потока; u, u – соответственно продольная и поперечная компоненты скорости; zn – отметка свободной поверхности потока; zд – отметка дна; l – коэффициент гидравлического трения; g – ускорение силы тяжести.
Для дифференцируемых функций, применяя к (26) теорему Гаусса – Остроградского, после некоторых преобразований получим уравнения Сен-Венана в дифференциальном виде:
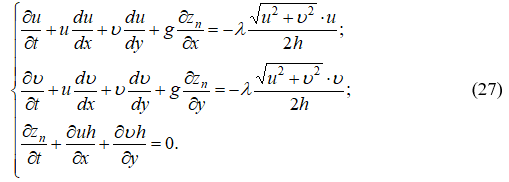
Для стационарных потоков и для 
получим:
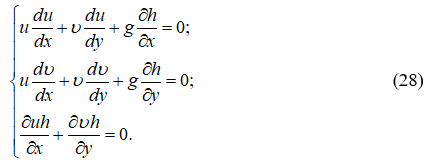
Эта система совпадает с точностью до обозначений компонент скорости с системой (11).
Приведём метод решения важной для практики задачи определения сопряжённых параметров струи двухмерного в плане бурного потока при её ударе о боковую стенку (рис. 1) на базе использования уравнений движения в интегральной форме.
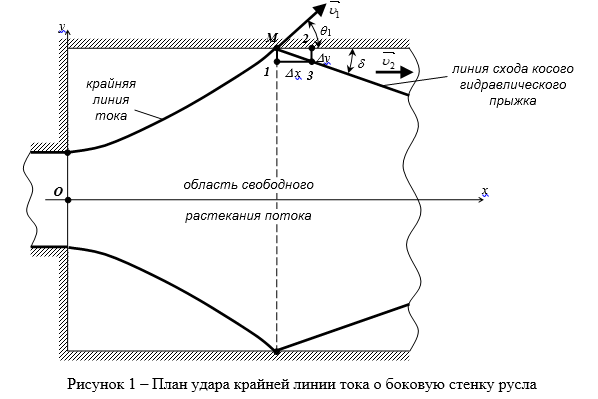
Пусть в точке M до удара крайней линии потока о боковую стенку русла он имеет параметры V1, h1, q1.
Необходимо определить параметры потока в точке M после удара V2, h2 и угол d отклонения линии схода от боковой стенки русла.
Для определения величин V2, h2, d воспользуемся уравнением стационарного движения потока в интегральной форме без учёта сил сопротивления потоку:
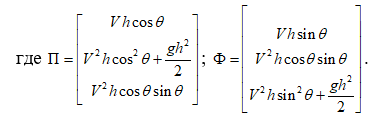
Составляя алгоритмическую форму уравнения применительно к четырёхточечному шаблону 1M23 (см. рис. 1), две точки которого находятся на линии схода, и разрешая её относительно параметров потока в точке M, получим алгебраическую систему:
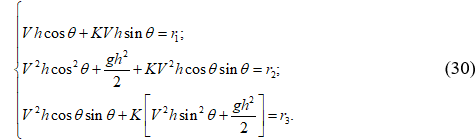
Так как до удара крайней линии тока о боковую стенку системе (30) должны удовлетворять параметры V1, h1, q1, то
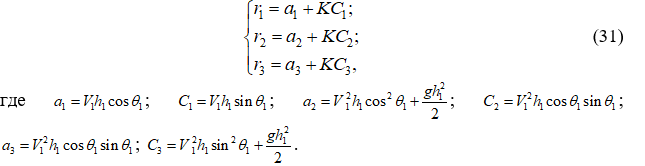
За прыжком в точке M угол 
и, следовательно, из системы (30) следует:
В системе (32) три неизвестных параметра V2, h2, K и для её совместности должно выполняться условие:
Определив из уравнения (33) неизвестное K, определим далее и сопряжённые параметры потока V2, h2, d за прыжком:
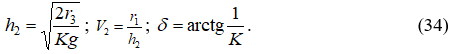
Ранее в литературе по гидравлическим расчётам для решения задачи определения параметров V2, h2, d необходимо было пользоваться громоздкими номограммами, имеющими ограничения 
, что сильно затрудняло получение достоверного результата.
Выводы. Исследователи в области моделирования течений двухмерных в плане открытых водных потоков могут воспользоваться уравнениями движения потока в зависимости от решаемой задачи в любой форме, изложенной в настоящей работе, и получить результаты моделирования с точностью, превышающей известную по ранее используемым методам. Особенно удобен метод расчёта потенциальных потоков с использованием плоскости годографа скорости.
1. Emcev B.T. Dvuhmernye burnye potoki. - M.: Energiya, 1967. - 212 s.
2. Vysockiy L.I. Upravlenie burnymi potokami na vodosbrosah. - M.: Energiya, 1990. - 280 s.
3. Korn G., Korn T. Spravochnik po matematike dlya nauchnyh rabotnikov i inzhenerov. - M.: Nauka, 1970. - 720 s.
4. Arsenin V.Ya. Metody matematicheskoy fiziki i special'nye funkcii. - M.: Nauka, 1984. - 384 s.
5. Tihonov A.N., Samarskiy A.A. Uravneniya matematicheskoy fiziki. - M.: Nauka, 1986. - 106 s.
6. Esin A.I. Razvitie teorii i metodov rascheta stacionarnyh i nestacionarnyh dvizheniy vody: Avtoref. diss. na soisk. uch. step. d-ra tehn. nauk: 05.23.16. - M., 2004. - 48 s.
7. Esin A.I. Zadachi tehnicheskoy mehaniki zhidkosti v estestvennyh koordinatah / FGOU VPO «Saratovskiy GAU». - Saratov, 2003. - 144 s.
8. Chaplygin S.A. Izbrannye trudy / Mehanika zhidkosti i gaza. Matematika. Obschaya mehanika. - M.: Nauka, 1976. - 496 s.
9. Kohanenko V.N., Volosuhin Ya.V. i dr. Modelirovanie odnomernyh i dvuhmernyh otkrytyh vodnyh potokov / NGMA; V.N. Kohanenko, Ya.V. Volosuhin, V.V. Shiryaev, N.V. Kohanenko; pod obsch. red. d-ra tehn. nauk, prof. V.N. Kohanenko. - Rostov n/D: Izd-vo YuFU, 2007. - 168 s.
10. Kohanenko V.N., Volosuhin Ya.V. i dr. Modelirovanie burnyh dvuhmernyh v plane vodnyh potokov: monografiya / V.N. Kohanenko, Ya.V. Volosuhin, M.A. Lemeshko, N.G. Papchenko; pod obsch. red. d-ra tehn. nauk, prof. V.N. Kohanenko. - Rostov n/D: Izd-vo YuFU, 2013. - 180 s.
11. Shiryaev V.V., Micik M.F. i dr. Razvitie teorii dvuhmernyh otkrytyh vodnyh potokov: monografiya / V.V. Shiryaev, M.F. Micik, E.V. Duvanskaya; pod obsch. red. V.V. Shiryaeva. - Shahty: Izd-vo YuRGUES, 2007. - 133 s.
12. Shterenliht D.V. Gidravlika. / Izd. 3-e, pererab. - M.: Kolos, 2005. - 656 s.
13. Spravochnik po gidravlike / Pod red. V.A. Bol'shakova. Izd. 2-e, pererab. i dop. - K.: Vischa shkola, 1984. - 343 s.
14. Militeev A.N., Togunova N.P. Metod rascheta sopryazheniya b'efov v prostranstvennyh usloviyah / Gidravlika sooruzheniy orositel'nyh sistem: tr. NIMI. - Novocherkassk, 1976. - T. 18. - Vyp. 5. - S. 180-194.
15. Weiming Wu, M.ASCE Depth-Averaged Two-Dimensional Numerical Modeling of Unsteady Flow and Nonuniform Sediment Transport in Open Channels // Journal of Hydraulic Engineering Vol. 130, Issue 10 (October 2004) doi:https://doi.org/10.1061/(ASCE)0733-9429(2004)130:10(1013)
