employee
Rostov-na-Donu, Rostov-on-Don, Russian Federation
employee
Rostov-na-Donu, Rostov-on-Don, Russian Federation
Don State Technical University (Undergraduate)
Donskoy gosudarstvennyy tenicheskiy universitet
Russian Federation
Russian Federation
GRNTI 67.23 Архитектурно-строительное проектирование
GRNTI 67.01 Общие вопросы строительства
OKSO 270000 АРХИТЕКТУРА И СТРОИТЕЛЬСТВО
BBK 382 Изыскания и проектирование в строительстве
BBK 308 Монтаж, эксплуатация, ремонт машин и промышленного оборудования
TBK 5414 Строительные конструкции
The evolution of the formation of a rotative surface formed by an arbitrary spatial curve by rolling without sliding the moving torso along the fixed torso is studied. The optimum form for creation of unique architectural appearance of a construction is received. The finite element model of the building of parametric architecture by the finite element method is developed. To confirm the correctness of the design solutions, the dynamic calculation and analysis of the obtained frequencies and eigenfrequencies were performed.
parametric architecture, rotative surface, finite element method, finite element model
Исследована эволюция формообразования ротативной поверхности, образованной произвольной пространственной кривой качением без скольжения подвижного торса по неподвижному торсу [1-2]. Производящая кривая совершает ротативное движение, при котором бесконечно малые последовательные перемещения кривой будут перемещениями вращения вокруг непрерывно изменяющейся оси [3]. Торсы, при помощи которых происходит движение производящей кривой линии, называются подвижными и неподвижными аксоидами. Плоскость, цилиндр, конус и прямая линия являются частными видами торса. Не любое сочетание аксоидов дает возможность осуществить ротативное движение - торс может катиться без скольжения только по своему изгибанию. Существует десять возможных сочетаний неподвижного и подвижного аксоидов: прямая – плоскость; плоскость – конус; плоскость – цилиндр; плоскость – торс; конус – плоскость; конус – конус; цилиндр – плоскость; цилиндр – цилиндр; торс – плоскость; торс – торс (Рис. 1). Конус и цилиндр, цилиндр и торс не могут составить пар аксоидов для ротативного движения.
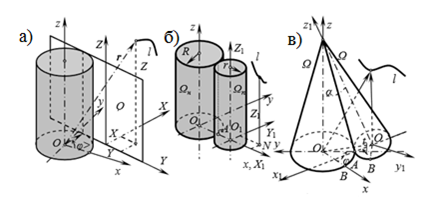
Рис 1. Ротативные поверхности: а) аксоиды «цилиндр-плоскость»;
б) аксоиды «цилиндр-цилиндр»; в) аксоиды «конус-конус»
Параметрическая форма поверхности описывается следующими функциями:
X= XU* (cos(f)*cos(v)*cos(n*v)-sin(v)*sin(n*v))+ZU*sin(f)*cos(v);
Y= XU*(cos(f)*sin(v)*cos(n*v)+cos(v)*sin(n*v))+ZU*sin(f)*sin(v);
Z= XU*cos(n*v)*sin(f)-ZU*cos(f);
Переменные: XU=-b*(u-c)*(u-c)/(c*c)+b; ZU=a+u,
где b – радиус кривизны оболочки;
с –растяжение оболочки по высоте;
n - количество выпуклых частей поверхности в плоскости XY;
а - ширина раскрытия оболочки по верхнему контуру;
f - отношение углов наклона поверхности к образующей.
Формообразование поверхности с помощью генератора линий и поверхностей в ПК САФИР представлено на рис. 2.
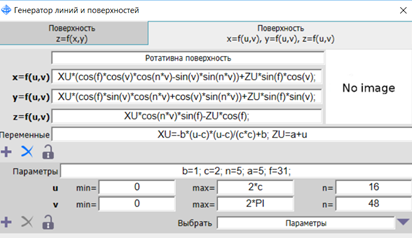
Рис 2. Генератор линий и поверхностей в ПК САФИР
Изменение формообразования поверхности при изменении отношения углов наклона поверхности к образующей показано на рис.3.
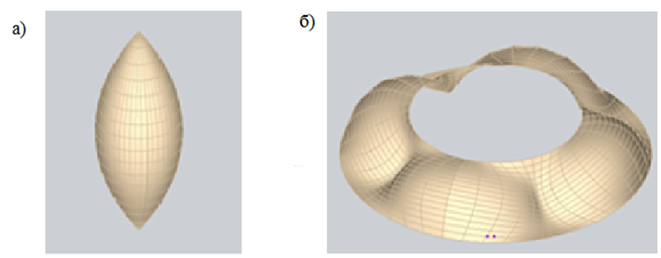
Рис. 3. Формообразование по параметру f: а) f =0 ; б) f=1
Методом итераций подобрано оптимальное соотношение углов наклона. Для дальнейшего исследования формообразования принято отношение Sinα/Sinφ=31 (Рис. 4).
Рис. 4. Формообразование при f=31
На следующем этапе определена ширина раскрытия оболочки по верхнему контуру (Рис. 5). Окончательно принято значение параметра а=5.
Рис. 5. Формообразование по ширине раскрытия оболочки: а) а=0; б) а=5
Параметром n регулируется количество выпуклых частей поверхности в плоскости XY. Для проектирования объекта параметрической архитектуры принята поверхность с пятью выпуклыми частями (Рис. 6).
Рис. 6. Варьирование количеством выпуклых частей: а) n=3; n=5
В результате получена оболочка диаметром 90 м и высотой 45 м.
Для разработки конструктивной схемы объекта и рационального использования внутреннего пространства оболочки необходимо убрать пазухи, образованные на внутренней поверхности ребер [4-5]. Оболочка импортирована и доработана в программном комплексе АutoCAD (Рис. 7).
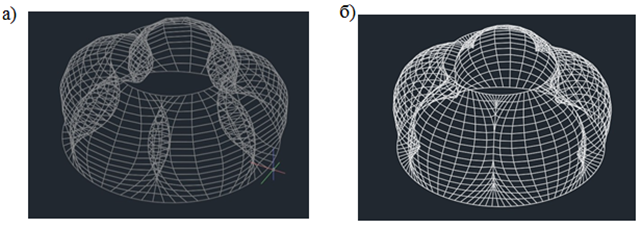
Рис. 7. Оболочка в ПК AutoCAD: а) до обработки; б) после обработки
Полученные результаты экспортированы в ПК САПФИР и приняты за исходные данные при разработке конструктивных решений (Рис. 8).
Рис. 8. Поверхность в ПК«САПФИР»: а) вариант конструктивных решений; б) расчетная схема
Каркас здания выполнен из монолитных железобетонных колонн и плит перекрытий. Толщина плит перекрытий – 200 мм, колонны диаметром 600 мм на нижних этажах, далее 500 мм с уменьшением до 400 мм. Каркас оболочки включает балки из стальных горячекатаных двутавров №18.
Конечно-элементная модель разработана в ПК Лира-САПР [6]. При создании использованы универсальные пространственные стержни, четырех узловые оболочки и одноузловые конечный элемент с упруго податливой связью (Рис. 9).
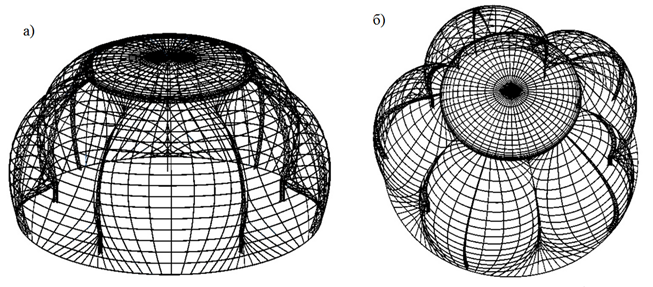
Рис. 9. Конечно-элементная модель каркаса здания: а) вид 1; б) вид 2
Для проверки правильности конструктивных решений выполнен динамический расчет каркаса здания [7-8]. Исследованы частоты и формы свободных колебаний конечно-элементной модели, дающие представление о возможных способах деформирования конструкции (Рис. 10). На этапе проектирования модальный анализ позволяет уточнить принятые значения геометрических и физических характеристик каркаса [9].
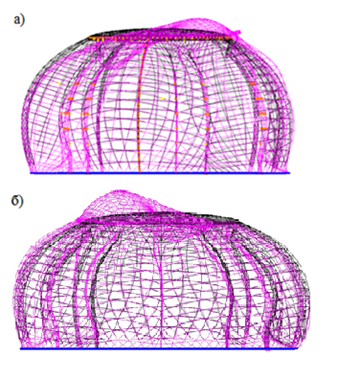
Рис. 9. Формы колебаний каркаса: а) 1-я форма; б) 3-я форма
В результате динамического расчета получены главные формы собственных колебаний, частоты и перемещения в узлах. Первая и вторая формы собственных колебаний – поступательная; третья – крутильная; четвертая - изгибно-крутильная. Полученная последовательность характера форм собственных колебаний подтверждает рациональность каркаса сооружения [10].
Итак, исследование эволюции формообразования объекта параметрической архитектуры позволяет выбрать оптимальный вариант аналитической ротативной поверхности для проектирования уникального сооружения. Моделирование объектов параметрической архитектуры методом конечных элементов приводит к созданию каркаса сооружения отвечающего требованиям прочности, надежности и экономичности проектных решений.
1. Ebeling V., Engel' A., Fajstel' R.. Fizika processov evolyucii. Per.nem. YU. A. Danilova. M.: Editorial URSS, 2001. 328 p.
2. Stessel' S.A. Zaimstvovanie prirodnyh principov formoobrazovaniya v parametricheskoj arhitekture // Vektor nauki TGU. 2015. №2. S. 52-57.
3. Krivoshapko S.N., Ivanov V.N., Halabi S.M. Analiticheskie poverhnosti: materialy po geometrii 500 poverhnostej i informaciya k raschetu na prochnost' tonkih obolochek. M.: Nauka, 2006. 544 p.
4. Kravchenko G.M., Manojlenko A. YU., Litovka V.V. Primenenie parametricheskogo proektirovaniya pri modelirovanii metodom konechnyh elementov // Inzhenernyj vestnik Dona, 2019, №3.
5. Kravchenko G.M., Trufanova E.V., Kochura V.G. Informacionnoe modelirovanie ob"ekta parametricheskoj arhitektury. Izvestiya vysshih uchebnyh zavedenij. Severo-Kavkazskij region. Seriya: Tekhnicheskie nauki. 2019. № 1 (201). p. 17-22.
6. Agahanov E.K. O razvitii kompleksnyh metodov resheniya zadach mekhaniki deformiruemogo tverdogo tela. Vestnik Dagestanskogo gosudarstvennogo tekhnicheskogo universiteta. Tekhnicheskie nauki. - 2013. - № 2. - p. 39-45.
7. Agahanov E.K., Kravchenko G.M., Trufanova E.V. Regulirovanie parametrov sobstvennyh kolebanij prostranstvennogo karkasa zdaniya //Vestnik Dagestanskogo gosudarstvennogo tekhnicheskogo universiteta. Tekhnicheskie nauki, - 2016. - № 3. - p. 8-15.
8. Agahanov E. K., Kravchenko G. M., Osadchij E.V., Trufanova E.V. Raschet zdanij slozhnoj geometricheskoj formy na vetrovye vozdejstviya. Vestnik Dagestanskogo gosudarstvennogo tekhnicheskogo universiteta. Tekhnicheskie nauki. - 2017. - № 2. - p. 8-17.
9. Savost'yanov V.N., Agahanov E.K. Ob ekvivalentnosti vozdejstvij v staticheskoj zadache mekhaniki deformiruemogo tverdogo tela. Izv. Vuzov. Stroitel'stvo. - 1995. - № 10. - p. 26-30.
10. Kravchenko G.M., Trufanova E.V., Tronin D.I., Gunba A.E.Issledovanie dinamicheskih harakteristik karkasa zdaniya metodom konechnyh elementov. Stroitel'stvo i arhitektura. 2019. T. 7. № 1. p. 39-44.
