Rostov-na-Donu, Rostov-on-Don, Russian Federation
Rostov-on-Don, Russian Federation
from 01.09.2018 until now
Rostov-na-Donu, Rostov-on-Don, Russian Federation
GRNTI 67.23 Архитектурно-строительное проектирование
GRNTI 67.01 Общие вопросы строительства
OKSO 270000 АРХИТЕКТУРА И СТРОИТЕЛЬСТВО
BBK 8511 Архитектура
BBK 308 Монтаж, эксплуатация, ремонт машин и промышленного оборудования
TBK 852 Архитектура
Modern trends in parametric architecture take us away from the use of static surfaces, pushing the dynamics to the first place. A new approach to architecture is opened, based on the dynamic development of shaping. The desire to develop the most optimal ratio of strength and expended material leads to an assessment of the prospects for the use of minimal and one-sided surfaces. Using the example of varying the parameters of a onesided Klein surface, the evolution of a parametric object from a simple Mobius strip to a complex dynamic form is demonstrated. The formation of the analytical surface in various software packages was studied. The sphere of applicability of various stages of form evolution to architectural objects is established.
parametric architecture, analytic surface, bionics, Klein surface, evolution
Потребности архитекторов, дизайнеров и инженеров-проектировщиков в инновационном формообразовании ставят вопрос о движении в архитектуре. Стационарная архитектура не в состоянии реагировать на факторы окружающей среды.
Средства вычислительного проектирования помогли установить связь между параметрическим и имитационным моделированием, что позволило анализировать поведение сооружения в течение времени. [1]
Архитекторы могут оценить поведение объекта, будь то здание, город, ландшафт или инфраструктура. Открывается новый подход в архитектуре, основанный на динамическом развитии формообразования [2]. Идея производительности становится прецедентом для формирования поверхности, а архитектурная форма - перформативным аспектом.
Для сбора качественных и количественных аспектов эффективности архитектурных артефактов на ранних стадиях дизайна необходимо оптимизировать форму, используя различные вычислительные инструменты.
За последние 5 лет появилось множество монографий [3,4], научных статей [5,6], в которых анализируются возможности применения канонических и неканонических аналитических поверхностей, подразделяющихся на различные типы и подклассы. В энциклопедии [7] представлены 500 поверхностей, заданных в параметрической, векторной и неявной формах, их которых не более 5% используются в архитектуре. Наиболее широко применяются поверхности вращения и пологие оболочки переноса, распространен гиперболоид, как формообразующая покрытия большепролетных сооружений. Менее популярны зонтичные поверхности и линейчатые поверхности различной гауссовой кривизны. Однако, современные тренды параметрической архитектуры отводят нас от использования статических поверхностей, выдвигая на первое место динамику. Стремление выработать наиболее оптимальное соотношение прочности и затраченного материала подводит к оценке перспектив использования минимальных и односторонних поверхностей.
Минимальная поверхность, у которой средняя кривизна равна нулю во всех точках, идеальна для тонкостенных конструкций. Поверхность сооружения должна быть замкнутой и определять целиком скелет здания. На замкнутой h-связной поверхности можно провести h-1 замкнутых кривых, не разбивающих поверхность. Поверхность, пересекающая саму себя, является односторонней поверхностью. Для наглядности представим, что вдоль замкнутой кривой на гладкой поверхности, находящейся в некотором пространстве, движется вектор нормали. Если при возвращении вектора в исходную точку его направление противоположно исходному, перед нами односторонняя замкнутая поверхность. Очевидно, что если вектор пройдет ещё один круг вдоль замкнутой кривой, то направление вектора совпадёт с исходным.
Простейшей односторонней поверхностью является лента Мебиуса. Для моделирования ленты Мебиуса достаточно взять длинную бумажную полоску и склеить противоположные концы, предварительно перевернув один из них. Лента Мебиуса является символом динамики формы, подчеркивая цикличность движения, и используется как международный символ переработки отходов. (рис 1.)
Рис. 1. Международный символ переработки отходов в форме ленты Мебиуса
Если затрагивать вопросы экономичности и экологии объекта, то предложенные классы поверхностей позволяют создать тонкостенные оболочки, требующие минимальных затрат материала. Процесс формообразования объекта параметрической архитектуры и дальнейшей оптимизации обеспечен возможностью создания таких поверхностей в большинстве расчетных комплексов.
Такой подход предполагает создание структурного скелета из облегченных элементов, конструируя сложные узлы сопряжения, используя BIM-технологии [8].
Сооружения, использующие аналитические поверхности, считают уникальными с точки зрения формы, а не принятой классификации, заложенной в определение уникальных зданий в разных странах. Объекты параметрической архитектуры привлекают инвесторов, положительно влияют на развитие туризма.
Для исследования применения поверхности Клейна к проектированию зданий и сооружений выполнен анализ минимальных и односторонних поверхностей. Выявлено, что поверхность Клейна в виде замкнутой односторонней поверхности без особых точек является идеальным отображением ленты Мебиуса в объеме. Существует несколько работ, посвященных исследованию математических свойств поверхности Клейна [9,10].
Параметрическая форма задания поверхности Клейна:
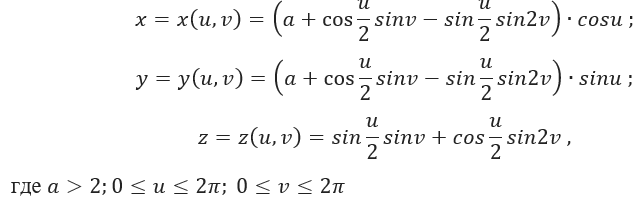
Классический вид соответствует следующим параметрам:
где nu и nv - количество шагов табуляции переменных u и v соответственно.
Задание параметров поверхности выполнено в программном комплексе SCAD (рис 2).
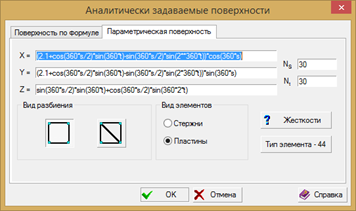
Рис. 2. Задание параметров аналитической поверхности
На рис.3 представлена параметрическая поверхность, которая может быть использована при проектировании здания с атриумом внутри.
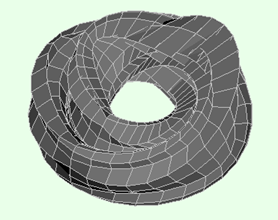
Рис. 3. Параметрическая поверхность при а=2.1
При увеличении параметра а с постоянной табуляцией и диапазоном u и v, возрастает радиус внутреннего свободного пространства (рис.4).
Рис. 4. Параметрическая поверхность при а=5
При отсутствии атриума следует снизить параметр а до значения, меньше либо равном 1. Уменьшение количества шагов табуляции nv до 10 позволяет упростить сетку элементов и получить качественно новую форму поверхности. Для сравнения объект параметрической архитектуры воспроизведен в ПК ЛИРА (САПФИР-3Д) (рис. 5).
Рис. 5. Поверхность Клейна при а=1, nv=10 в ПК SCAD, ЛИРА соответственно
Уменьшение диапазона значений v в два раза позволяет получить форму, близкую к бионике. (рис. 6). Поверхность, параметр v которой принимает значения от 0 до π, симметрична по горизонтальной плоскости поверхности, параметр v которой принимает значения от π до 2π (рис 7).
Рис. 6. Поверхность Клейна при а=2.1, 0≤v≤π в ПК SCAD, ЛИРА соответственно
Функциональное назначение полученного объекта параметрической архитектуры выставочное или торговое пространство, ведущее посетителей вдоль траектории развития поверхности.
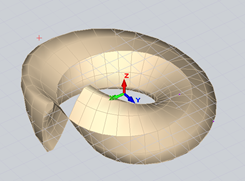
Рис. 7. Поверхность Клейна при а=2.1, π≤v≤2π в ПК ЛИРА
Отсюда следует, что при варьировании параметров u и v важна разность максимальных и минимальных значений параметров, а не их конкретные значения (рис 8).
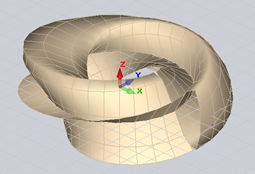
Рис. 8. Поверхность Клейна при а=2.1, -0.125π≤v≤1.25π в ПК ЛИРА
Поверхности со значениями параметров, не кратными π, не представляют интереса для практического применения, так как выглядят незавершенными, что противоречит концепции бионики.
Концепция бионики включает принцип минимизации затрат в реализуемых технических объектах и принцип разнообразия форм, который широко используется в параметрической архитектуре. Варьирование параметров аналитической поверхности неслучайно привело к формам, совпадающим с теми, что создала природа, копируя параметры живых организмов. Объект параметрической архитектуры предполагает разработку дополнительных оптимальных конструктивных решений каркаса.
Концепция параметризма включает эволюцию архитектурных объектов в соответствии с жизненным циклом объектов живой природы.
Отличие полученных форм поверхности Клейна в ПК SCAD и ЛИРА подчеркивает необходимость разработки современных комплексов, ресурсы которых могут быть использованы архитекторами и проектировщиками при развитии параметрической архитектуры.
Эволюция поверхности Клейна демонстрирует поведение объекта параметрической архитектуры в динамике от простой ленты Мебиуса до бионической формы, являющейся инновационным способом представления пространства.
Варьирование параметров поверхности Клейна позволило выявить многофункциональность, что дает основание для применения ее в качестве формообразующей к уникальным и перспективным объектам. Попытка применения поверхности Клейна к формообразованию зданий и сооружений предпринята впервые.
Итак, исследовано формообразование поверхности Клейна в различных программных комплексах. Анализ результатов позволяет сделать вывод о том, что при варьировании параметров u и v важна разность максимальных и минимальных значений параметров, а не их конкретные значения. Поверхность Клейна может быть использована как при проектировании сооружений с большим внутренним свободным пространством, так и объектов, пространство которых задает направление траектории развития. Функциональное назначение зданий с аналитической поверхностью Клейна – выставочные и торговые павильоны, в которых обтекаемая форма сооружения обеспечивает оптимальную организацию потоков большого количества людей.
В дальнейшем предполагается развитие концепции параметрической архитектуры в направлении совмещения аналитической поверхности и структурного скелета зданий и сооружений.
1. Lenka Kormaníková et al: Shape Design and Analysis of Adaptive Structures, Procedia Engineering 190 (2017) pp 7 - 14.
2. E. Reyssat1and, L. Mahadevan, Hygromorphs: From pine cones to biomimetic bilayers, Journal of The Royal Society Interface. 6 (2009) pp 951-957.
3. Krivoshapko S.N., Mamieva IA. Analiticheskie poverhnosti v arhitekture zdanii: konstrukciy i izdeliy: Monografiya. - M.: Knizhnyy dom «LIBROKOM», 2012. - 328 s.
4. Krasic Sonja. Geometrijske povrsi u arhitekturi. - Gradevinsko- arhitektonski fakultet Univerzitet u Nisu. - Stampa Galaksija: Nis, 2012 - 238 c.
5. Hyeng Christian A. Bock, Yamb E.B. Application of cyclic shells in architecture, ma¬chine design, and bionics International Journal of Modern Engineering Researches. - 2012. - Vol. 2.-Iss.3.-P.799-806.
6. Grin'ko EA. Obzornye raboty po geometrii, prochnosti, ustoychivosti, dina¬mike i primeneniyu obolochek so sredinnymi poverhnostyami razlichnyh klassov// Montazhnye i special'nye raboty v stroitel'stve. - 2012. - № 2. - S. 15-21.
7. Krivoshapko C.H., Ivanov B.H. Enciklopediya analiticheskih poverhnostey. - M.: Knizhnyy dom «LIBROKOM», 2010. - 560 s.
8. Manav Mahan Singh et al: Modular coordination and BIM: Development of rule based smart building components / Procedia Engineering 123 (2015) pp 519 - 527.
9. Gou nakamura. Compact non-orientable surfaces of genus 4 with extremal metric discs / An Electronic Journal of the American Mathematical Society Volume 13, Pages 124-135 (April 22, 2009).
10. C. Bagi´nski, G. Gromadzki. Permutations of the boundary of Klein surfaces / RACSAM (2012) 106: pp 359-369.
