Ростов-на-Дону, Ростовская область, Россия
Ростовская область, Россия
с 01.09.2018 по настоящее время
Ростов-на-Дону, Ростовская область, Россия
ГРНТИ 67.23 Архитектурно-строительное проектирование
ГРНТИ 67.01 Общие вопросы строительства
ОКСО 270000 АРХИТЕКТУРА И СТРОИТЕЛЬСТВО
ББК 8511 Архитектура
ББК 308 Монтаж, эксплуатация, ремонт машин и промышленного оборудования
ТБК 852 Архитектура
Современные тренды параметрической архитектуры отводят нас от использования статических поверхностей, выдвигая на первое место динамику. Открывается новый подход в архитектуре, основанный на динамическом развитии формообразования. Стремление выработать наиболее оптимальное соотношение прочности и затраченного материала подводит к оценке перспектив использования минимальных и односторонних поверхностей. На примере варьирования параметров односторонней поверхности Клейна продемонстрирована эволюция параметрического объекта от простой лентой Мебиуса к сложной динамической форме. Исследовано формообразование аналитической поверхности в различных программных комплексах. Установлена сфера применимости различных стадий эволюции формы к архитектурным объектам.
параметрическая архитектура, аналитическая поверхность, бионика, поверхность Клейна, эволюция
Потребности архитекторов, дизайнеров и инженеров-проектировщиков в инновационном формообразовании ставят вопрос о движении в архитектуре. Стационарная архитектура не в состоянии реагировать на факторы окружающей среды.
Средства вычислительного проектирования помогли установить связь между параметрическим и имитационным моделированием, что позволило анализировать поведение сооружения в течение времени. [1]
Архитекторы могут оценить поведение объекта, будь то здание, город, ландшафт или инфраструктура. Открывается новый подход в архитектуре, основанный на динамическом развитии формообразования [2]. Идея производительности становится прецедентом для формирования поверхности, а архитектурная форма - перформативным аспектом.
Для сбора качественных и количественных аспектов эффективности архитектурных артефактов на ранних стадиях дизайна необходимо оптимизировать форму, используя различные вычислительные инструменты.
За последние 5 лет появилось множество монографий [3,4], научных статей [5,6], в которых анализируются возможности применения канонических и неканонических аналитических поверхностей, подразделяющихся на различные типы и подклассы. В энциклопедии [7] представлены 500 поверхностей, заданных в параметрической, векторной и неявной формах, их которых не более 5% используются в архитектуре. Наиболее широко применяются поверхности вращения и пологие оболочки переноса, распространен гиперболоид, как формообразующая покрытия большепролетных сооружений. Менее популярны зонтичные поверхности и линейчатые поверхности различной гауссовой кривизны. Однако, современные тренды параметрической архитектуры отводят нас от использования статических поверхностей, выдвигая на первое место динамику. Стремление выработать наиболее оптимальное соотношение прочности и затраченного материала подводит к оценке перспектив использования минимальных и односторонних поверхностей.
Минимальная поверхность, у которой средняя кривизна равна нулю во всех точках, идеальна для тонкостенных конструкций. Поверхность сооружения должна быть замкнутой и определять целиком скелет здания. На замкнутой h-связной поверхности можно провести h-1 замкнутых кривых, не разбивающих поверхность. Поверхность, пересекающая саму себя, является односторонней поверхностью. Для наглядности представим, что вдоль замкнутой кривой на гладкой поверхности, находящейся в некотором пространстве, движется вектор нормали. Если при возвращении вектора в исходную точку его направление противоположно исходному, перед нами односторонняя замкнутая поверхность. Очевидно, что если вектор пройдет ещё один круг вдоль замкнутой кривой, то направление вектора совпадёт с исходным.
Простейшей односторонней поверхностью является лента Мебиуса. Для моделирования ленты Мебиуса достаточно взять длинную бумажную полоску и склеить противоположные концы, предварительно перевернув один из них. Лента Мебиуса является символом динамики формы, подчеркивая цикличность движения, и используется как международный символ переработки отходов. (рис 1.)

Рис. 1. Международный символ переработки отходов в форме ленты Мебиуса
Если затрагивать вопросы экономичности и экологии объекта, то предложенные классы поверхностей позволяют создать тонкостенные оболочки, требующие минимальных затрат материала. Процесс формообразования объекта параметрической архитектуры и дальнейшей оптимизации обеспечен возможностью создания таких поверхностей в большинстве расчетных комплексов.
Такой подход предполагает создание структурного скелета из облегченных элементов, конструируя сложные узлы сопряжения, используя BIM-технологии [8].
Сооружения, использующие аналитические поверхности, считают уникальными с точки зрения формы, а не принятой классификации, заложенной в определение уникальных зданий в разных странах. Объекты параметрической архитектуры привлекают инвесторов, положительно влияют на развитие туризма.
Для исследования применения поверхности Клейна к проектированию зданий и сооружений выполнен анализ минимальных и односторонних поверхностей. Выявлено, что поверхность Клейна в виде замкнутой односторонней поверхности без особых точек является идеальным отображением ленты Мебиуса в объеме. Существует несколько работ, посвященных исследованию математических свойств поверхности Клейна [9,10].
Параметрическая форма задания поверхности Клейна:
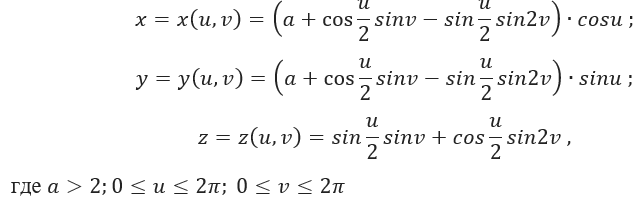
Классический вид соответствует следующим параметрам:
![]()
где nu и nv - количество шагов табуляции переменных u и v соответственно.
Задание параметров поверхности выполнено в программном комплексе SCAD (рис 2).
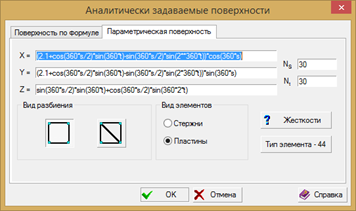
Рис. 2. Задание параметров аналитической поверхности
На рис.3 представлена параметрическая поверхность, которая может быть использована при проектировании здания с атриумом внутри.
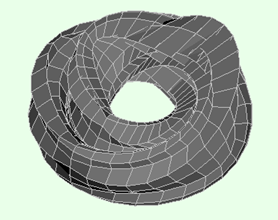
Рис. 3. Параметрическая поверхность при а=2.1
При увеличении параметра а с постоянной табуляцией и диапазоном u и v, возрастает радиус внутреннего свободного пространства (рис.4).

Рис. 4. Параметрическая поверхность при а=5
При отсутствии атриума следует снизить параметр а до значения, меньше либо равном 1. Уменьшение количества шагов табуляции nv до 10 позволяет упростить сетку элементов и получить качественно новую форму поверхности. Для сравнения объект параметрической архитектуры воспроизведен в ПК ЛИРА (САПФИР-3Д) (рис. 5).

Рис. 5. Поверхность Клейна при а=1, nv=10 в ПК SCAD, ЛИРА соответственно
Уменьшение диапазона значений v в два раза позволяет получить форму, близкую к бионике. (рис. 6). Поверхность, параметр v которой принимает значения от 0 до π, симметрична по горизонтальной плоскости поверхности, параметр v которой принимает значения от π до 2π (рис 7).

Рис. 6. Поверхность Клейна при а=2.1, 0≤v≤π в ПК SCAD, ЛИРА соответственно
Функциональное назначение полученного объекта параметрической архитектуры выставочное или торговое пространство, ведущее посетителей вдоль траектории развития поверхности.
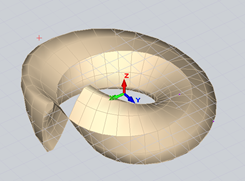
Рис. 7. Поверхность Клейна при а=2.1, π≤v≤2π в ПК ЛИРА
Отсюда следует, что при варьировании параметров u и v важна разность максимальных и минимальных значений параметров, а не их конкретные значения (рис 8).
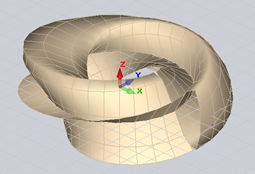
Рис. 8. Поверхность Клейна при а=2.1, -0.125π≤v≤1.25π в ПК ЛИРА
Поверхности со значениями параметров, не кратными π, не представляют интереса для практического применения, так как выглядят незавершенными, что противоречит концепции бионики.
Концепция бионики включает принцип минимизации затрат в реализуемых технических объектах и принцип разнообразия форм, который широко используется в параметрической архитектуре. Варьирование параметров аналитической поверхности неслучайно привело к формам, совпадающим с теми, что создала природа, копируя параметры живых организмов. Объект параметрической архитектуры предполагает разработку дополнительных оптимальных конструктивных решений каркаса.
Концепция параметризма включает эволюцию архитектурных объектов в соответствии с жизненным циклом объектов живой природы.
Отличие полученных форм поверхности Клейна в ПК SCAD и ЛИРА подчеркивает необходимость разработки современных комплексов, ресурсы которых могут быть использованы архитекторами и проектировщиками при развитии параметрической архитектуры.
Эволюция поверхности Клейна демонстрирует поведение объекта параметрической архитектуры в динамике от простой ленты Мебиуса до бионической формы, являющейся инновационным способом представления пространства.
Варьирование параметров поверхности Клейна позволило выявить многофункциональность, что дает основание для применения ее в качестве формообразующей к уникальным и перспективным объектам. Попытка применения поверхности Клейна к формообразованию зданий и сооружений предпринята впервые.
Итак, исследовано формообразование поверхности Клейна в различных программных комплексах. Анализ результатов позволяет сделать вывод о том, что при варьировании параметров u и v важна разность максимальных и минимальных значений параметров, а не их конкретные значения. Поверхность Клейна может быть использована как при проектировании сооружений с большим внутренним свободным пространством, так и объектов, пространство которых задает направление траектории развития. Функциональное назначение зданий с аналитической поверхностью Клейна – выставочные и торговые павильоны, в которых обтекаемая форма сооружения обеспечивает оптимальную организацию потоков большого количества людей.
В дальнейшем предполагается развитие концепции параметрической архитектуры в направлении совмещения аналитической поверхности и структурного скелета зданий и сооружений.
1. Lenka Kormaníková et al: Shape Design and Analysis of Adaptive Structures, Procedia Engineering 190 (2017) pp 7 - 14.
2. E. Reyssat1and, L. Mahadevan, Hygromorphs: From pine cones to biomimetic bilayers, Journal of The Royal Society Interface. 6 (2009) pp 951-957.
3. Кривошапко С.Н., Мамиева ИА. Аналитические поверхности в архитектуре здании: конструкций и изделий: Монография. - М.: Книжный дом «ЛИБРОКОМ», 2012. - 328 с.
4. Krasic Sonja. Geometrijske povrsi u arhitekturi. - Gradevinsko- arhitektonski fakultet Univerzitet u Nisu. - Stampa Galaksija: Nis, 2012 - 238 c.
5. Hyeng Christian A. Bock, Yamb E.B. Application of cyclic shells in architecture, ma¬chine design, and bionics International Journal of Modern Engineering Researches. - 2012. - Vol. 2.-Iss.3.-P.799-806.
6. Гринько ЕА. Обзорные работы по геометрии, прочности, устойчивости, дина¬мике и применению оболочек со срединными поверхностями различных классов// Монтажные и специальные работы в строительстве. - 2012. - № 2. - С. 15-21.
7. Кривошапко C.H., Иванов B.H. Энциклопедия аналитических поверхностей. - М.: Книжный дом «ЛИБРОКОМ», 2010. - 560 с.
8. Manav Mahan Singh et al: Modular coordination and BIM: Development of rule based smart building components / Procedia Engineering 123 (2015) pp 519 - 527.
9. Gou nakamura. Compact non-orientable surfaces of genus 4 with extremal metric discs / An Electronic Journal of the American Mathematical Society Volume 13, Pages 124-135 (April 22, 2009).
10. C. Bagi´nski, G. Gromadzki. Permutations of the boundary of Klein surfaces / RACSAM (2012) 106: pp 359-369.


















