Moscow, Russian Federation
Russian Federation
Lyubercy, Russian Federation
Poluchena formula dlya rascheta progiba staticheski opredelimoy ploskoy fermy pod deystviem ravnomerno raspredelennoy nagruzki. Usiliya v sterzhnyah opredelyayutsya metodom vyrezaniya uzlov. Progib v zavisimosti ot chisla paneley nayden po formule Maksvella – Mora s primeneniem metoda indukcii i sistemy komp'yuternoy matematiki Maple
Fermaferma, progib, kinematicheskoe vyrozhdenie, formula Maksvella- –Mora, Maple
На рис. 1 и 2 приведены два варианта одной и той же схемы решетчатой симметричной фермы при разных числах панелей n = 2k. Схемы почти неотличимы, однако в первом случае это статически определимая неизменяемая ферма, во втором — мгновенно изменяемая конструкция. Выяснить это в общем случае коварное свойство конструкции удалось при выводе формулы прогиба фермы методом индукции [6]. Оказалось, что если число панелей k в половине пролета кратно 7, то определитель матрицы уравнений равновесия узлов обращается в ноль. Аналогичный эффект был обнаружен в плоских фермах [2; 3] и в пространственной ферме [5].
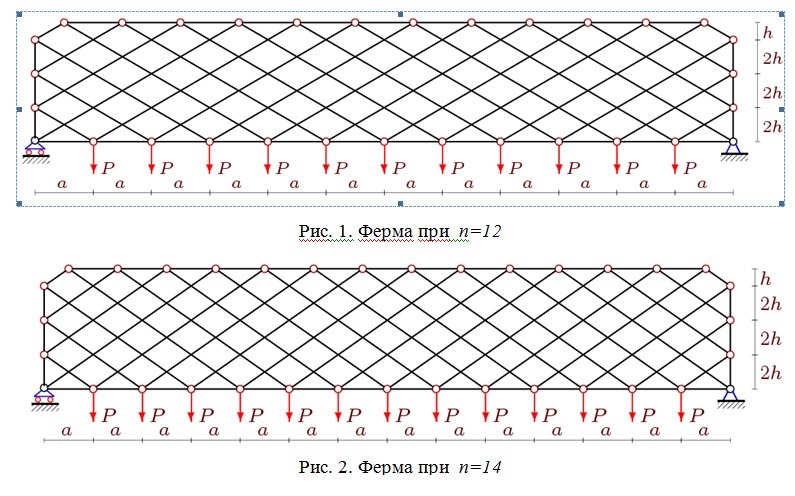
Приведем весь алгоритм вывода прогиба фермы. За прогиб примем вертикальное смещение среднего узла нижнего пояса. Рассмотрим случай действия равномерной по нижнему поясу нагрузки. Ферма содержит 2n + 7 узлов, m = 4n + 14 стержней. В это число входят n стержней нижнего пояса, 6 боковых стоек, n + 1 стержней верхнего пояса, 2n + 4 раскосов и 3 опорные опорных стержня. Усилия в стержнях рассчитываются методом вырезания узлов по программе [54]. Для ввода данных фермы в программу необходимо ввести координаты узлов. Начало координат расположено в левой подвижной опоре. В системе Maple ввод выглядит следующим образом:

1. Kirsanov M.N., Maslov A.N. Formuly dlya rascheta progiba balochnoj mnogoreshetchatoj fermy [The formula for calculation of the deflection of multiple lattice beam truss] Stroitel'naya mekhanika i raschet sooruzhenij. 2017. 2(271). pp. 4-10.
2. Kirsanov M.N. Ocenka progiba i ustojchivosti prostranstvennoj balochnoj fermy [Evaluation of deflection and stability of spatial girder] Stroitel'naya mekhanika i raschet sooruzhenij. 2016. № 5 (268). pp. 19-22.
3. Jiang H., Kirsanov M.N. An analytical expression for the influence line of the truss. Vestnik nauchnyh konferencij. 2016. № 1-5 (5). pp. 10-11. DOI:https://doi.org/10.17117/cn.2016.01.05
4. Kirsanov M.N. Reshebnik. Teoreticheskaya mekhanika/Pod red. A.I.Kirillova [Solver. Theoretical mechanics] Moscow: Fizmatlit, 2008. 382 p.
5. Tin'kov D.V. Sravnitel'nyj analiz analiticheskih reshenij zadachi o progibe fermennyh konstrukcij [Comparative analysis of analytical solutions to the problem of deflection of truss structures] Inzhenerno-stroitel'nyj zhurnal. 2015. №5(57). pp. 66-73.
6. Kijko L.K. Analiticheskaya ocenka progiba arochnoj fermy pod dejstviem vetrovoj nagruzki [Analytical evaluation of deflection of arched trusses under wind load] Nauchnyj vestnik. 2016. № 1 (7). pp. 247-254.



















