г. Москва и Московская область, Россия
Россия
Люберцы, Россия
Получена формула для расчета прогиба статически определимой плоской фермы под действием равномерно распределенной нагрузки. Усилия в стержнях определяются методом вырезания узлов. Прогиб в зависимости от числа панелей найден по формуле Максвелла – Мора с применением метода индукции и системы компьютерной математики Maple
Фермаферма, прогиб, кинематическое вырождение, формула Максвелла- –Мора, Maple
На рис. 1 и 2 приведены два варианта одной и той же схемы решетчатой симметричной фермы при разных числах панелей n = 2k. Схемы почти неотличимы, однако в первом случае это статически определимая неизменяемая ферма, во втором — мгновенно изменяемая конструкция. Выяснить это в общем случае коварное свойство конструкции удалось при выводе формулы прогиба фермы методом индукции [6]. Оказалось, что если число панелей k в половине пролета кратно 7, то определитель матрицы уравнений равновесия узлов обращается в ноль. Аналогичный эффект был обнаружен в плоских фермах [2; 3] и в пространственной ферме [5].
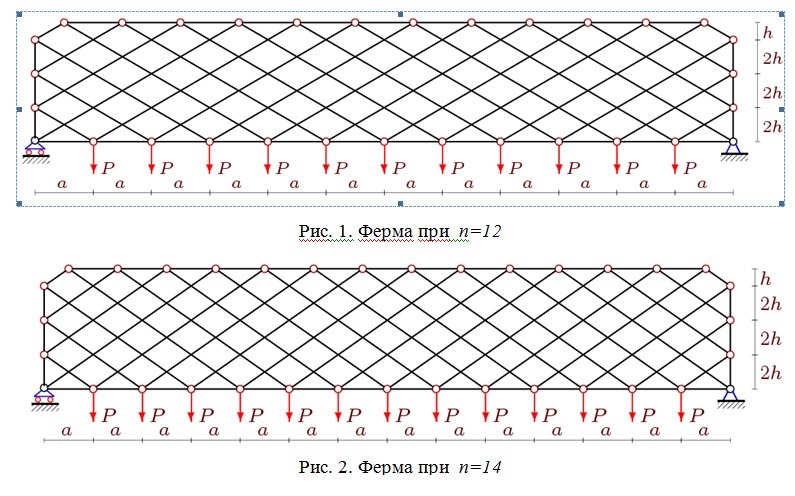
Приведем весь алгоритм вывода прогиба фермы. За прогиб примем вертикальное смещение среднего узла нижнего пояса. Рассмотрим случай действия равномерной по нижнему поясу нагрузки. Ферма содержит 2n + 7 узлов, m = 4n + 14 стержней. В это число входят n стержней нижнего пояса, 6 боковых стоек, n + 1 стержней верхнего пояса, 2n + 4 раскосов и 3 опорные опорных стержня. Усилия в стержнях рассчитываются методом вырезания узлов по программе [54]. Для ввода данных фермы в программу необходимо ввести координаты узлов. Начало координат расположено в левой подвижной опоре. В системе Maple ввод выглядит следующим образом:

1. Кирсанов М.Н., Маслов А.Н. Формулы для расчета прогиба балочной многорешетчатой фермы//Строительная механика и расчет сооружений. 2017. 2(271). С. 4-10.
2. Кирсанов М.Н. Оценка прогиба и устойчивости пространственной балочной фермы//Строительная механика и расчет сооружений. 2016. № 5 (268). С. 19-22.
3. Jiang H., Kirsanov M.N. An analytical expression for the influence line of the truss// Вестник научных конференций. 2016. № 1-5 (5). С. 10-11. DOI:https://doi.org/10.17117/cn.2016.01.05
4. Кирсанов М.Н. Решебник. Теоретическая механика/Под ред. А.И.Кириллова -М.: Физматлит, 2008. 382 с.
5. Тиньков Д.В. Сравнительный анализ аналитических решений задачи о прогибе ферменных конструкций // Инженерно-строительный журнал. 2015. №5(57). С. 66-73.
6. Кийко Л.К. Аналитическая оценка прогиба арочной фермы под действием ветровой нагрузки // Научный вестник. 2016. № 1 (7). С. 247-254.



















