Ростов-на-Дону, Ростовская область, Россия
Россия
Московский технический университет связи и информатики, Северо-Кавказский филиал (Кафедра «Информатика и вычислительная техника»)
Россия
УДК 68 Различные отрасли промышленности и ремесла
ГРНТИ 50.13 Технология и оборудование для производства средств автоматики и вычислительной техники
ББК 3297 Вычислительная техника
В монографии рассмотрено современное состояние вопроса создания нечетко-логических оптических устройств, служащих для разработки высокоэффективных экспертных систем, которые будут обеспечивать запросы специалистов из самых различных областей. Применение аппарата нечетких систем обусловлено тенденцией увеличения сложности математических и формальных моделей реальных систем и процессов управления, связанной с желанием повысить их адекватность и учесть все большее число различных факторов, оказывающих влияние на процессы принятия решений. Основные направления приведенных в монографии исследований направлены на разработку основных элементов оптического компьютера. Авторами данной работы было запатентовано свыше 50 различных нечетко-логических оптических устройств и способов обработки информации с их использованием, многие из которых подробно рассмотрены в данной монографии. Написание книги было инициировано задачами, сформулированными в рамках проекта СМАРТ (Спутниковый Мониторинг – Активному Развитию Территорий), где рассматривается ряд принципиальных проблем, включая адаптивность принятия управленческих решений. Книга предназначена для научных работников, специалистов, аспирантов и магистрантов, специализирующихся в области фотоники, разработки нечетко – логических методов и устройств, а также для студентов старших курсов физико-математических факультетов и инженерных вузов по соответствующим специальностям.
Нечетко-логические оптические процессоры, нечетко-логические системы и устройства, элементы оптических нечетко-логических процессоров, оптические фаззификаторы, конъюнкторы и дизъюнкторы, оптические нечетко-логические функциональные преобразователи, оптоэлектронные дефаззификаторы, современные способы обработки цифровой информации
ВВЕДЕНИЕ
В современной действительности нечеткое моделирование и применение аппарата нечетких систем является одним из наиболее перспективных направлений прикладных исследований в области управления и принятия решений. Нечеткое моделирование и управление оказываются особенно полезными, когда в описании технических систем и технологических процессов присутствует неопределенность, которая затрудняет или даже исключает применение точных количественных методов и подходов для принятия решений.
В настоящей работе рассмотрено современное состояние вопроса создания нечетко-логических оптических устройств, служащих для разработки высокоэффективных экспертных систем, обеспечивающих запросы специалистов самых различных областей информации.
Востребованность применения аппарата нечетких систем обусловлена тенденцией увеличения сложности математических и формальных моделей реальных систем и процессов управления, связанной с желанием повысить их адекватность и учесть все большее число различных факторов, оказывающих влияние на процессы принятия решений.
Авторами данной работы было запатентовано свыше 50 различных нечетко-логических оптических устройств и способов обработки информации с их использованием [3,4, 27 - 66], многие из которых подробно рассматриваются ниже.
Решение проблем использования нечетко-логических оптических устройств и способов обработки информации с их использованием было инициировано задачами, поставленными в рамках проекта СМАРТ (Спутниковый Мониторинг – Активному Развитию Территорий), где рассматривается ряд принципиальных проблем, включая адаптивность принятия управленческих решений и задачу создания объединенных информационных ресурсов, формируемых различными системами и структурами (данные дистанционного зондирования Земли из космоса (ДЗЗ), информация стационарного и мобильного мониторинга для органов местного самоуправления, муниципальных предприятий жизнеобеспечения, объектов социальной сферы, сельхозтоваропроизводителей, организаций и органов охраны правопорядка и ликвидации чрезвычайных ситуаций и др.).
Решение таких сложных задач зачастую базируется на одновременном использовании целого ряда универсальных информационно – коммуникационных платформ:
- инструментального типа для формирования и использования систем интегрированных геопространственных данных и данных формирования информационного пространства;
- интеллектуального типа - платформы сбора данных, охватывающие стационарные и мобильные комплексы видеонаблюдения (с распознаванием), георадарное оборудование, автоматизированные лаборатории, информацию от различных датчиков, информацию от приборов учета, показания высокотехнологичного медицинского оборудования для телемедицины, данные ДЗЗ, включающие модели для тематического дешифрирования и др.;
- аналитического типа для формирования и анализа ресурсов ГИС-схем планирования развития территорий: интерактивные 3D-ГИС модели, модели топологии транспортных инженерных систем и систем телекоммуникаций, балансные модели «актив-ресурс-проект» и др.
С одной стороны, традиционные методы построения моделей не приводят к удовлетворительным результатам, когда исходное описание подлежащей решению проблемы заведомо является неточным или неполным. С другой стороны, стремление получить всю исчерпывающую информацию для построения точной математической модели сложной реальной ситуации может привести к потере времени и средств, поскольку это может быть в принципе невозможно.
В подобных случаях наиболее целесообразно воспользоваться такими методами, которые специально ориентированы на построение моделей, учитывающих неполноту и неточность исходных данных. Именно в таких ситуациях технология нечеткого управления оказывается наиболее конструктивной, что объективно подтверждено появлением огромного числа устройств для сбора и обработки информации в системах автоматизации и управления технологическими процессами, промышленным производством, решения социальных приложений.
Нечеткая логика, которая служит основой для реализации методов управления, более естественно описывает характер человеческого мышления и ход его рассуждений, чем традиционные формально-логические системы. Именно поэтому использование математических средств для представления нечеткой исходной информации позволяет строить модели, которые наиболее адекватно отражают различные аспекты неопределенности, постоянно присутствующие в окружающей нас реальности.
Сегодня для построения любых систем управления (как автоматизированных, так и автоматических) требуются эффективные, надежные и недорогие технические средства, которые могли бы осуществлять выполнение нечетких алгоритмов управления в реальном масштабе времени с высокой точностью вычисления.
В настоящее время техническую базу реализации нечетких технологий составляют микропроцессорные средства и микроконтроллеры, аналоговые и аналого-цифровые СБИС. Однако микропроцессоры и однокристальные микроконтроллеры не способны в полной мере реализовать все потенциальные возможности нечеткой логики по следующим объективным причинам:
- их быстродействие ограничено в части реализации ряда сложных нечетких операторов из-за последовательной обработки данных, присущей современным микропроцессорным средствам;
- погрешность вычислений с течением времени постоянно растет из-за неизбежных методических ошибок, обусловленных использованием цифровых методов вычисления;
- в микропроцессорных системах обработки нечеткой информации с увеличением значений базовых шкал нечетких переменных происходит нелинейное увеличение времени выполнения операций над элементами термов этих переменных, а также этапов фаззификации и дефаззификации; в свою очередь, увеличение значений базовых шкал нечетких множеств ведет к неизбежному увеличению областей памяти микропроцессорных реализаций для хранения и обработки данных, что ведет к увеличению времени выполнения вычислительных операций.
Кроме того, существующие микропроцессорные системы обработки нечеткой информации обладают значительными габаритами, массой и потребляемой мощностью.
При применении же цифро-аналоговых СБИС для конструирования нечетких процессоров разработчики будут неизбежно сталкиваться с проблемой разброса параметров аналоговых интегральных микросхем, что может существенно сказываться на стоимости разработки систем и устройств за счет применения дополнительных схемно-технических решений для стабилизации параметров и характеристик приборов. Также могут возникнуть трудности и в процессе эксплуатации таких средств – за счет разбалансировки параметров приборов, трудностей регулировки параметров аналоговых устройств, дрейфа рабочих точек, более низких показателей надежности аналоговых устройств по сравнению с цифровыми и пр.
На сегодняшний день известны устройства, альтернативные электронным - построенные на основе оптических методов обработки информации, в частности, методов Фурье-оптики и Фурье-голографии. Но эти методы, в свою очередь, достаточно трудно реализуемы и не позволяют обеспечить весь комплекс операций над нечеткими множествами и отношениями, что не дает возможности осуществить нечетко-логический вывод в целом.
Поэтому возникает задача разработки методов проектирования и создания совершенно нового класса вычислительных устройств, обладающих значительным быстродействием, надежностью, простотой настройки параметров, меньшей конструктивной сложностью и реализующих при этом принципы нечеткой логики с сохранением точности выполняемых вычислений на произвольном интервале времени.
В связи с этим, в настоящей книге исследуются методы синтеза устройств, базирующихся на способах представления информации, ориентированных на оптическую природу ее носителя, и реализующие вычислительные операции аппарата нечетких систем практически в реальном времени.
Глава 1. Анализ состояния современных нечетких систем и перспектив их развития.
1.1 Нечеткая логика в слабо формализованных задачах принятия решений
Традиционный подход к решению задач теории систем управления на основе существующих в прикладной математике формально-логических методов ставит своей целью создание точных (в широком смысле слова) моделей строгих рассуждений и выводов. Основное внимание здесь приходится уделять вопросам корректности, полноты, непротиворечивости, замкнутости, устойчивости, управляемости и многим другим качественным аспектам описания моделей объектов и алгоритмов управления. Вопрос же оценки истинности утверждения логических высказываний типа «математическая модель адекватна реальному объекту управления» остается при этом, по существу, открытым и не может быть решен только в рамках принятого метода исследования.
Построение моделей динамических систем как объектов управления представляет собой одну из основных задач теории автоматического управления [84]. Основное содержание этой задачи состоит в решении проблем описания процессов, происходящих в объектах и САУ, выбора соответствующих методов формализации и установления соответствия (адекватности) получаемых таким образом моделей с исходным объектом, а также с методами исследования (в зависимости от уровня физической и математической строгости). Особое место здесь занимают методы синтеза устройств для моделирования и фильтрации случайных процессов [16].
Следует отметить, что процесс построения моделей физических процессов носит сложный эволюционный характер; связан с неизбежной аппроксимацией реального объекта и приводит к потере информации при его описании. При этом гипотезы и аксиомы, по которым осуществляется аппроксимация и описание реального объекта соответствующей моделью, могут не учитывать реальной сущности физического процесса, что приводит к дополнительному приращению риска и неопределенности в описании объекта управления.
С точки зрения теории нечетких моделей здесь рассматриваются два варианта [6, 85]: 1) нечеткость описания, как аппроксимация слабо структурированной и слабо формализованной модели реального объекта управления из-за его сложности и неопределенности информации о его свойствах; 2) объективная внутренняя нечеткость функционирования, которой обладает любой реальный объект.
В последние два десятилетия резко возрос интерес к различным аспектам проблемы интеллектуального управления, (см., например, [6, 12]). Одно из основных направлений, связанных с решением этой проблемы, состоит в использовании аппарата нечетких систем: нечетких множеств, нечеткой логики, нечеткого моделирования и т.п.
Применение этого аппарата приводит к построению нечетких систем управления различных классов, позволяющих решать задачи управления в ситуациях, когда традиционные методы неэффективны или даже вообще неприменимы из-за отсутствия достаточно точного знания об объекте управления [67].
Основу нечетких моделей САУ в общем случае представляют собой нечеткие логические регуляторы (НЛР), которые широко применяются при создании робототехнических комплексов, АСУТП, гибких производственных систем управления сложными динамическими системами и др. НЛР используют в своей основе модели нечеткой логики: модели нечеткой импликации и композиционного правила вывода. Для нечетких регуляторов, использующих реализацию соответствующей модели продукционного нечеткого логического вывода на основе нечеткого продукционного процессора, традиционна следующая схема лингвистического описания: операторы перевода в нечеткие значения (фаззификаторы), нечеткая импликация, нечеткие модификаторы, нечеткие логические связки, композиционное правило вывода и операторы перевода в четкие значения (дефаззификаторы).
Основу проектирования интеллектуальных нечетких регуляторов составляет конструирование «базы знаний» с использованием методов представления и поиска знаний. Структура интеллектуальной системы управления динамическими технологическими процессами или объектами с нечетким регулятором представляет собой структуру классической замкнутой САУ, осуществляющей управление по отклонению, где в качестве регулятора применяется НЛР. Такая структура представлена на рисунке 1.1.
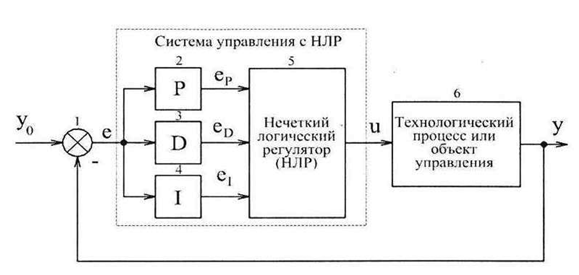
Рис. 1.1. Структура интеллектуальной системы управления динамическими технологическими процессами или объектами с нечетким регулятором
Выходная переменная у технологического процесса (или параметр объекта управления) 6 сравнивается с ее заданным значением у0 в инвертирующем сумматоре 1 и ошибка рассогласования е поступает на входы блоков пропорциональности (масштабирования) 2, дифференцирования 3 и интегрирования 4. На выходе последних формируются сигналы, пропорциональные величине самой ошибки еР, ее производной еD и первообразной еI. Далее еР , еD и еI поступают в главный элемент системы управления - в НЛР 5, который вырабатывает на основе поступивших данных управляющее воздействие на технологический процесс (объект управления) 6. Показанная на рис. 1.1 система управления с НЛР, по сути, является так называемым нечетким ПИД-регулятором, используемым традиционно для управления динамическими технологическими процессами или объектами. Если управляемые технологические процессы и (или) объекты являются статическими, т.е. изменения параметров процесса (объекта) являются относительно медленными и некритичны к выбору управляющего воздействия, то в структуре системы управления с НЛР (рис. 1.1), не используются блоки дифференцирования 3 и интегрирования 4. В общем случае представление знаний в управляющих системах в теории искусственного интеллекта осуществляется логическими, реляционными, фреймовыми и продукционными языками. Учитывая такую важную специфику работы систем автоматического регулирования, как режим работы в реальном времени и удобство представления информации о процедурах и условиях их применения, на практике в основном используется продукционная модель описания знаний в нечетких регуляторах. Каждая продукция представляется в виде набора правил, представляющих собой фрагмент знаний — ядро в инженерии знаний. Она имеет вид «условие — действие».
Более сложный вариант фрагмента знаний «ситуация — стратегия управления — действие» рассмотрен в [21]. В общем случае структура нечеткого логического регулятора представляет собой структуру нечеткой модели, подробно описанной в [67] и показанной на рис. 1.2.
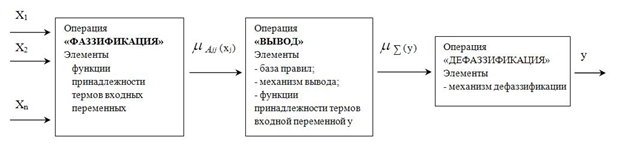
Рис. 1.2 Структура нечеткой модели
На входы нечеткой модели подаются четкие числовые значения Х1, Х2,…, Хn. Блок, выполняющий операцию или этап «ФАЗЗИФИКАЦИЯ» - далее фаззификатор, вычисляет значение степени принадлежности входной переменной Хi входным нечетким множествам Аij (i=1, 2,.., m; j = 1, 2,.., n). То есть фаззификатор переводит четкие значения входных переменных в их лингвистические значения. Для выполнения указанной операции блок фаззификации должен иметь доступ к точно определенным функциям принадлежности ![]() (хj) входов (i=1, 2,.., m; j = 1, 2,.., n).
(хj) входов (i=1, 2,.., m; j = 1, 2,.., n).
Блок, выполняющий операцию или этап «ВЫВОД» - далее блок вывода, на входе получает значения функций принадлежности ![]() (хj) и на выходе вычисляет т. н. результирующую (аккумулированную) функцию принадлежности
(хj) и на выходе вычисляет т. н. результирующую (аккумулированную) функцию принадлежности ![]() выходного значения модели. Данная функция обычно имеет сложную форму и определяется посредством вывода, который может быть осуществлен множеством способов [67]. Для выполнения вычислений блок вывода должен включать в себя следующие строго определенные элементы:
выходного значения модели. Данная функция обычно имеет сложную форму и определяется посредством вывода, который может быть осуществлен множеством способов [67]. Для выполнения вычислений блок вывода должен включать в себя следующие строго определенные элементы:
- база правил или т. н. база знаний;
- механизм вывода;
- функции принадлежности выходного параметра у.
База правил содержит логические правила, которые задают имеющие место в системе причинно-следственные отношения между нечеткими значениями ее входных и выходных величин. Как правило, база знаний нечетких регуляторов строится на основе продукционной модели знаний, имеющей конструкцию вида «если..., то...». Каждая продукция, представляющая собой множество пар «ситуация - действие», позволяет ставить в соответствии со сложившейся ситуацией действие регулятора в виде значения регулирующего воздействия на объект. База правил может иметь, например, следующий вид:
Правило 1: ЕСЛИ х1 есть А11 И Х2 есть А12 И..И хn есть А1n, ТО у есть В1;
Правило 2: ЕСЛИ х1 есть А21 И Х2 есть А22 И..И хn есть А2n,
ТО у есть В2;
…………
Правило i : ЕСЛИ х1 есть Аi1 И Х2 есть Аi2 И..И хn есть Аin,
ТО у есть Вi;
………
Правило m: ЕСЛИ х1 есть Аm1 И Х2 есть Аm2 И..И хn есть Аmn, ТО у есть Вm;
где х1 , х2,.., хn – n входных переменных нечеткой продукционной системы;
Аij - терм j-й входной переменной Xj в i-м правиле, представленный нечетким множеством с соответствующей функцией принадлежности ![]() (хj) (i=1, 2,.., m; j = 1, 2,.., n);
(хj) (i=1, 2,.., m; j = 1, 2,.., n);
у - выходная переменная нечеткой продукционной системы;
Вi - терм выходной переменной у в i -м правиле, представленный нечетким множеством с соответствующей функцией принадлежности ![]() (i=1, 2,.., m).
(i=1, 2,.., m).
Решение возложенной на блок вывода задачи, связанной с определением результирующей функции принадлежности ![]() , обеспечивается механизмом вывода, который состоит из следующих элементов:
, обеспечивается механизмом вывода, который состоит из следующих элементов:
- элемент, выполняющий операцию агрегирования - процесса определения степени истинности условия (антецедента) аi в каждом i-м правиле базы знаний (i=1, 2,.., m);
- элемент, выполняющий операцию активизации - процесса определения модифицированной функций принадлежности ![]() выходной переменной у в заключении (консеквенте) каждого i -го правила базы знаний;
выходной переменной у в заключении (консеквенте) каждого i -го правила базы знаний;
- элемент, выполняющий операцию аккумулирования – процесса определения результирующей функции принадлежности ![]() выходной переменной у путем объединения модифицированных нечетких множеств В'i по каждому i-му правилу базы знаний.
выходной переменной у путем объединения модифицированных нечетких множеств В'i по каждому i-му правилу базы знаний.
Блок, выполняющий операцию или этап «ДЕФАЗЗИФИКАЦИЯ» - далее дефаззификатор, на основе результирующей функции принадлежности ![]() вычисляет четкое числовое значение у выходного параметра, являющееся результатом для входных числовых значений х1 , х2,.., хn. Данная операция выполняется посредством механизма дефаззификации, который определяется соответствующим методом вычисления. Примеры механизмов дефаззификации приведены в [67], где также указывается, что к числу подходов, ориентированных на синтез нечетких регуляторов, относятся следующие:
вычисляет четкое числовое значение у выходного параметра, являющееся результатом для входных числовых значений х1 , х2,.., хn. Данная операция выполняется посредством механизма дефаззификации, который определяется соответствующим методом вычисления. Примеры механизмов дефаззификации приведены в [67], где также указывается, что к числу подходов, ориентированных на синтез нечетких регуляторов, относятся следующие:
- на основе знаний, полученных от экспертов;
- путем моделирования действий эксперта в качестве
регулятора (на основе управляющих сигналов, вырабатываемых экспертом); - на основе модели объекта управления.
Мировая практика разработки и использования систем с нечеткими регуляторами выявила ряд общих особенностей [85]:
- при исследовании и проектировании НЛР авторы не опирались на точную модель процесса. При этом интуиция разработчика, его знания о процессе непосредственно учитывались в алгоритме управления. Далее следовал итерационный процесс, заключающийся в проверке функционирования алгоритма, изучения его поведения и последующей модификации соответствующих управляющих правил. Часто это процедура требует значительных затрат времени;
- нечеткие подмножества включали лингвистические переменные, например, «положительно большой» или «отрицательно малый», что отражает общий подход к выбору определенных интервалов квантованных величин;
- как правило, во всех НЛР использовался основополагающий принцип регулирования - принцип регулирования по отклонению.
Перспективным направлением в развитии теории нечеткого управления и НЛР является создание адаптивных и самообучающихся нечетких систем. В работе [67] рассматриваются проблемы адаптивного нечеткого управления и указывается, что если параметры управляемого технологического процесса или объекта меняются, то можно воспользоваться методами оперативной идентификации. На этой основе осуществляется непрерывная подстройка параметров нечеткого регулятора или отдельных его частей. Структура адаптивной системы с нечетким регулятором приведена на рисунке 1.3.
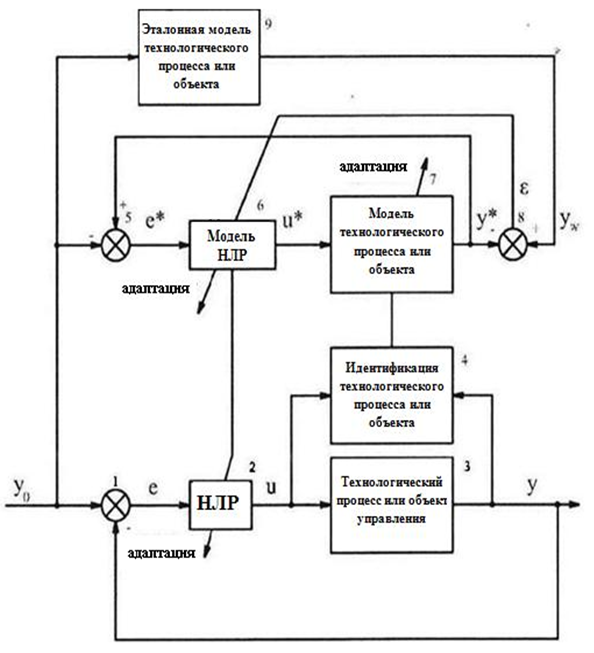
Рис. 1.3 Адаптивная система управления с НЛР
Нижняя часть данной структуры представляет собой замкнутую систему управления, состоящую из управляемого технологического процесса или объекта 3 и НЛР 2. Верхняя часть этой структуры — это модель реальной системы управления, включающая модель управляемого технологического процесса (или объекта) 7 и модель НЛР 6. Модель управляемого технологического процесса (или объекта) 7 настраивается на основе текущих значений замеров входного сигнала и выходного сигнала у. Обновленные значения параметров передаются в модель управляемого технологического процесса (или объекта) 7. Такая модификация (адаптация) параметров модели управляемого технологического процесса (или объекта) 7 активизирует алгоритм, настраивающий параметры модели НЛР 6. Для адаптации параметров модели НЛР 6 можно воспользоваться методом обратного распространения ошибки  , которая представляет собой разность между задающим (опорным) сигналом уW, вырабатываемым эталонной моделью управляемого технологического процесса (или объекта) 9 (определяет желаемое поведение системы управления в целом), и выходом у* модели управляемого технологического процесса (или объекта) 7. В конечном счете, модифицированные значения параметров модели управляемого технологического процесса 7 и модели НЛР 6 передаются в НЛР 2, который управляет рассматриваемым технологическим процессом (или объектом) 3. Описанная адаптация осуществляется непрерывно (оперативный режим), либо периодически. Отметим, что структура, изображенная на рисунке 1.3, состоит из двух последовательно соединенных и одновременно настраиваемых подсистем (настройка модели управляемого технологического процесса (объекта) 7 и модели НЛР 6). Таким образом, система может потерять устойчивость, особенно при быстром изменении значений параметров объекта. Следовательно, по соображениям безопасности, рассмотренную выше структуру адаптации можно применять для «медленных» объектов (в смысле изменения значений их параметров) или же при изменении параметров рассматриваемого объекта, проявляющихся от случая к случаю.
, которая представляет собой разность между задающим (опорным) сигналом уW, вырабатываемым эталонной моделью управляемого технологического процесса (или объекта) 9 (определяет желаемое поведение системы управления в целом), и выходом у* модели управляемого технологического процесса (или объекта) 7. В конечном счете, модифицированные значения параметров модели управляемого технологического процесса 7 и модели НЛР 6 передаются в НЛР 2, который управляет рассматриваемым технологическим процессом (или объектом) 3. Описанная адаптация осуществляется непрерывно (оперативный режим), либо периодически. Отметим, что структура, изображенная на рисунке 1.3, состоит из двух последовательно соединенных и одновременно настраиваемых подсистем (настройка модели управляемого технологического процесса (объекта) 7 и модели НЛР 6). Таким образом, система может потерять устойчивость, особенно при быстром изменении значений параметров объекта. Следовательно, по соображениям безопасности, рассмотренную выше структуру адаптации можно применять для «медленных» объектов (в смысле изменения значений их параметров) или же при изменении параметров рассматриваемого объекта, проявляющихся от случая к случаю.
Таким образом, резюмируя данный параграф, можно подчеркнуть, что применение нечетких алгоритмов в сочетании с принципами адаптации и самоорганизации позволяет улучшить процессы управления в экстремальных ситуациях и осуществить реализацию так называемых «щадящих» режимов работы вспомогательных аппаратов, а также повысить «гибкость» и «интеллектуальность» систем управления технологическими процессами и объектами.
1.2 Нечетко-логические устройства сбора и обработки информации в системах автоматизации управления технологическими процессами и производством
В период с
- в
- в
- в
Такая интенсификация разработок и соответствующих материальных затрат основана на тщательном планировании и подробном маркетинге. Данным процессам предшествовал длительный период (с 1970 по 1980 гг.) исследовательских работ по разработке методов анализа, синтеза, моделирования и проектирования оптимальных структур моделей нечетких регуляторов и систем управления [11, 85]. На сегодняшний день в основу аппаратной реализации структуры интеллектуальной системы управления с нечетким регулятором положен нечеткий процессор. В таких системах снижение уровня сложности структурной реализации и соответствующего программно-аппаратного обеспечения достигается за счет применения встраиваемых специализированных микропроцессорных модулей на СБИС (как прототипов ЭВМ шестого поколения на нечетком процессоре) с заданным нечетким логическим выводом.
Для обработки нечеткой лингвистической информации микропроцессорными специализированными СБИС требуются соответствующие блоки нечеткой памяти, обеспечивающие хранение нечетких слов (функция принадлежности нечеткого множества квантуется и представляется в виде n-элементного вектора, называемого нечетким словом) для осуществления многошагового нечеткого вывода.
Следует отметить, что аппаратную реализацию приближенных рассуждений в виде продукционных правил «если..., то...» с сотнями и тысячами нечетких импликаций трудно осуществлять в реальном времени на традиционных моделях ЭВМ. Поэтому соответствующие разработки инструментальных средств ведутся в направлении развития и усовершенствования элементной базы нечетких процессоров, а также структур самих процессоров (как специализированных нечетких ЭВМ, предназначенных для использования в автономном режиме или в качестве сопроцессора обычных ПЭВМ).
Самым первым разработанным цифровым нечетким процессором был FС 110 (фирмы Тоgаi Infra Lоgic, США) на основе кристалла (чипа) нечеткого логического вывода, который представляет собой высокоэффективный сопроцессор для применения методов нечеткой логики и реализации нечетких алгоритмов управления в реальном времени. Процессор FС 110 имеет на одном чипе 256 бит оперативной памяти; байтовый формат данных; набор машинных команд составлен из ограниченного числа сложных инструкций (модификация RISС-архитектуры). Введены специальные команды для оценки левой и правой логических частей нечетких продукционных правил «если …, то…», а также для построения сложных составных правил. При этом процессор FС 110 с рабочей частотой 10 МГц имеет скорость обработки правила 35 мкс, скорость вывода логических правил 28000 в 1 с (процессор 80386 с частотой 20 МГц имеет соответственно 400 мкс и 2300 правил в 1 с). Наиболее целесообразное применение спецпроцессора FС 110 - это нечеткий сопроцессор совместно с главной ЭВМ общего назначения, когда главный процессор выполняет все входные и выходные преобразования, а процессор FС 110 обеспечивает оценку состояния базы знаний. Символьный внутрисхемный эмулятор FС 1101 СЕ для процессора FС 110 создан для ускорения разработки, настройки и отладки прикладных интеллектуальных систем на нечеткой логике, в частности, для проектирования баз нечетких знаний экспертных систем. Примером эффективного применения процессора FС 110 является его использование в структуре нечеткого контроллера при решении задачи управления устойчивым состоянием перевернутого маятника [85]. Языком программирования для реализации базы нечетких знаний на нечетком процессоре FС 110 стал модифицированный нечеткий язык С, разработан также нечеткий язык программирования FРL. С системой разработки нечетких версий языка С можно объединить оболочки ТIL-shell для построения программ управления с использованием баз знаний, сформированных с помощью версии ТIL-shell. Сопроцессор FС 110 позволяет на базе ПЭВМ типа IВМ РС обрабатывать более 370 тыс. нечетких продукционных правил (с двумя посылками) в 1 с, а также более 1 млн. булевых продукционных правил в 1 с; в частности, подсистема VМЕ фирмы Тоgаi обладает быстродействием четырех PC, используя четыре параллельно соединенных чипа FС 110 [11, 85].
Известны также реализации нечеткого процессора на основе аналоговых СБИС, где достигается высокая скорость логического вывода продукционных правил (от 1 до 10 млн. нечетких логических правил в 1 с). Так, например, нечеткий процессор FUZ-М1 позволяет обрабатывать нечеткую информацию и осуществлять приближенные рассуждения в течение 100 нс; нечеткий регулятор (после поступления детерминированной информации) осуществляет процедуру управления на основе приближенного рассуждения. Здесь применяется СБИС, в которой на одном чипе реализуется нечеткое правило вывода типа обобщенного правила «Модус Поненс» [85].
Новый вид нечеткого логического процессора разработан с использованием квантовых эффектов (на основе управляемых квантовых переходов Джозефсона). Процессор реализует 60 логических правил, обрабатывает 4 переменных за 300 мкс (последнее означает наличие скорости логического вывода 2-10 логических правил в 1 с) и сочетает в себе технологию цифровой и аналоговой техники [85].
В Европе и США ведутся интенсивные работы по интеграции fuzzy-команд в ассемблеры промышленных контроллеров встроенных устройств (чипы Моtоrоlа 68НС11.12.21). Такие аппаратные средства позволяют в несколько раз увеличить скорость выполнения приложений и компактность кода по сравнению с реализацией на обычном ядре. Кроме того, разрабатываются различные варианты fuzzy-сопроцессоров, которые контактируют с центральным процессором через общую шину данных, концентрируют свои усилия на размывании/уплотнении информации и оптимизации использования правил (продукты Siemens Nixdorf).
Наиболее распространенными разработками инструментальных средств [85] для программно-аппаратного обеспечения нечетких регуляторов и систем управления являются: системы инструментальной поддержки и информационного обеспечения FRUITAX, экспертная система управления процессами обработки изображений LINK man, компьютерная диалоговая система супервизорного управления FLS, система автоматизированного проектирования процессов управления IFCS, системы конструирования программного обеспечения типа RРХ-FUZZY, FS-2000 и др. Hа основе данных инструментальных средств разработана серия нечетких регуляторов и систем управления типа FZ-1000 - FZ-5000, МIСRЕХ- F 250, МIСRЕХ- F 500, FОС-2001, FОС-2001A, FОС-2001АН, ЕХ-100, ЕХ-1000, EХ-1000/32, ЕХ- FUZZY, HX-1000 и мн. др. Также в [80] показаны примеры архитектур универсального нечеткого регулятора типа FZ—3000/3010 фирмы Оmron, используемого в станках с числовым программным управлением и нечеткого регулятора типа МIСRЕХ -500 фирмы Fuji Еlесtriс, используемого в системе управления подъемными кранами. Оба регулятора реализованы на инструментальных средствах FRUITAX. Для наглядности на рисунке 1.4 показана структурная схема нечеткого регулятора типа FZ—3000/3010 фирмы Оmron, используемого в станках с числовым программным управлением.
В общем случае нечеткий регулятор типа FZ—3000/3010 фирмы Оmron содержит: 1 - внешнее периферийное вычислительное устройство на базе ПЭВМ; 2 - аналоговую шину высокоскоростной передачи данных; 3 -арифметико-логическое устройство; 4 - блок памяти; 5 - устройство связи; 6 -блок цифрового ввода-вывода; 7 - блок нечеткого ввода-вывода; 8 - блок дефаззификации (выбора четкого значения); 9, 10 - блок нечеткого логического вывода; 11 - общую шину передачи цифрового сигнала; 12 - станок с числовым программным управлением.
Для подобных нечетких регуляторов разработаны рабочие станции для АРМ проектирования нечетких процессоров. Разработанные АРМ позволяют построить логические регуляторы, основу которых составляют нечеткие процессоры на СБИС. При этом по качеству переходных процессов и достижению целей управления построенные регуляторы превосходят традиционные П-, ПИ- и ПИД-регуляторы.
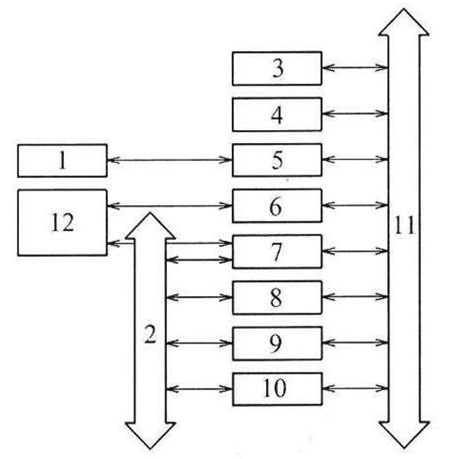
Рис. 1.4. Структура нечеткого регулятора типа FZ—3000/3010 фирмы Оmron
Среди отечественных разработок следует отметить специализированные аппаратные средства для реализации нечетких алгоритмов управления, созданные под руководством профессора А.Н.Мелихова [21]. В рамках этих исследований были достигнуты следующие результаты:
- разработаны теория, методы и алгоритмы преобразования нечеткой информации и знаний для проектирования нового поколения нечетких процессоров, контроллеров, ускорителей и компьютеров, позволяющих на основе нечеткой логики и нечеткой математики выполнять обработку четкой (цифровой) и нечеткой (качественной) информации и знаний;
- созданы методики проектирования нечетких компьютеров, способных выполнять логические (правдоподобные) рассуждения на основе оригинальных алгоритмов идентификации (распознавания) нечетких ситуаций;
- созданы аппаратные средства поддержки проектирования и функционирования интегральных систем обработки информации, принятия решений, ситуационного управления, распознавания, обучения, прогнозирования и других систем, являющихся интегральными помощниками человека в его профессиональной деятельности в различных предметных областях, позволяющих на единой логической базе выполнять вычислительные и качественные алгоритмы преобразования информации, что позволяет строить интеллектуальные системы, основанные как на известных способах представления накопления и преобразования знаний, так и на методах и алгоритмах представления и обработки нечеткой информации и знаний [21].
В середине 1980-х гг. были разработаны ряд лингвистических блоков, устройств и комплексов, позволяющих обрабатывать нечеткую информацию, реализовывать операции над нечеткими множествами, выполнять нечеткие алгоритмы управления - например, вычислительный комплекс обработки нечеткой информации на базе персональной ЭВМ, включающий специальный сопроцессор нечеткой информации, ориентированный на использование в человеко-машинных системах и системах искусственного интеллекта, а также ГПСС, представляющий собой комплекс программных средств автоматизации разработки и создания индивидуальных советующих систем на базе ПЭВМ [21], в основу конструирования технических средств которых, были положены следующие принципы:
- лингвистические вычислительные комплексы ориентированы на реализацию различных нечетких алгоритмов управления и состоят из лингвистических устройств и стандартных средств вычислительной техники;
- лингвистические устройства ориентированы на реализацию определенных нечетких алгоритмов или операций по преобразованию нечеткой информации и состоят из лингвистических блоков;
- лингвистические блоки ориентированы на реализацию элементарных алгоритмов различных операций над нечеткими множествами и нечеткими логическими переменными и состоят из стандартных элементов цифровой схемотехники (триггеры, сумматоры, мультиплексоры, схемы сравнения, регистровые структуры и т.д.) и элементов микропроцессорной техники с микропрограммным управлением;
- представление значений функции принадлежности осуществляется в виде однобайтовых чисел с фиксированной точкой с дискретностью от 0,01 до 0,005 (например, «,00000001» = 1/256 ~ 0,004; «,00110011» = 51/256 ~ 0,2; «,11111111» = 255/256 ~1);
- операции над независимыми друг от друга переменными, а также значениями функций принадлежности в интервале [0, 1], можно проводить параллельно путем введения аппаратной избыточности.
В 1995-
Процессор FuzСор 2.0 представляет собой нечеткий логический процессор, выполненный по технологии полузаказной СБИС, и имеет конвейерную архитектуру с векторным процессором. Его структурная схема приведена на рисунке 1.5.
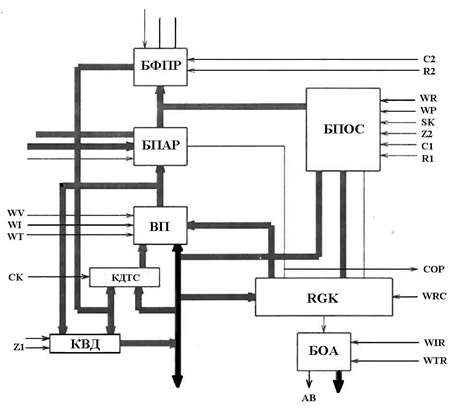
Рис. 1.5. Структурная схема нечеткого процессора FuzСор 2.0
Процессор FuzСор 2.0 состоит из векторного процессора (ВП), блока параллельного определения минимума или максимума (БПАР), блока формирования промежуточных результатов (БФПР), блока последовательного сравнения с порогом (БПОС), коммутатора данных текущей ситуации (КДТС), коммутатора выходных данных (КВД), блока определения адреса эталонной ситуации (БОА) и регистра команд (RGK).
Программной поддержкой процессора FuzСор 2.0 стал программный комплекс FuzЕх 2.0, предназначенный для проектирования систем, основанных на нечетких знаниях и использующих процессор нечеткого логического вывода FuzСор 2.0, либо его программный эмулятор для нечеткого логического вывода. В настоящее время в России работы по созданию оптоэлектронных процессоров нечеткой логики ведутся в ФИАН им. Лебедева, в ВЦ РАН и МЭИ, а также в Санкт-Петербургском государственном университете информационных технологий, механики и оптики. Так, в последнем, сотрудниками кафедры «Фотоники и оптоинформатики» были разработаны оптические технологии искусственного интеллекта, в частности, технологии реализации вычислительных операций, присущих нечеткой логике. Принципы выполнения вычислений в отношении операций нечеткой логики, подробно описанные в [1, 26], базируются на использовании алгебры Фурье-дуальных операторов, а сами оптические нечеткие процессоры физически реализуются схемами и устройствами, построенными на основе методов Фурье-оптики и Фурье-голографии.
Можно привести еще одну реализацию нечеткого оптического устройства. В работе [10] описан оптоэлектронный фаззификатор (рисунок 1.6, а), содержащий источник света, оптический канал передачи, ЭОД, блок ФП.
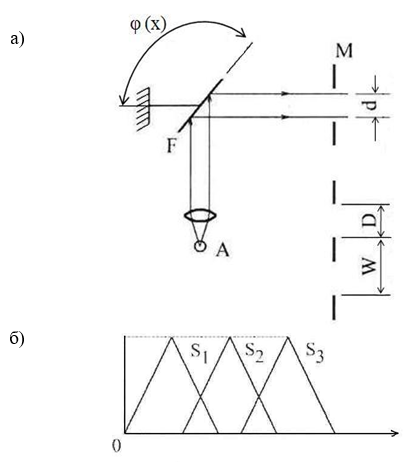
Рис. 1.6. Схема оптоэлектронного фаззификатора (а) и диаграмма площади засветки ФП (б)
Принцип действия оптоэлектронного фаззификатора состоит в следующем. Коллимированный луч света диаметром d от источника А отклоняется ЭОД таким образом, что засвечивает, в зависимости от угла ![]() , одно из отверстий маски М. Угол отклонения зеркала ЭОД
, одно из отверстий маски М. Угол отклонения зеркала ЭОД ![]() является функцией входной величины х. За маской устанавливаются либо фотоприемники, либо оптические элементы канализации света для передачи сигналов (при необходимости — после нормализации) на последующую обработку. Выходной функцией системы является площадь засветки ФП или входной апертуры оптической системы Si, где i - номер засвеченного oтверстия маски. При диаметре отверстий D = d, их шаге W =1,5D, постоянном расстоянии от ЭОД до маски, квадратных сечениях отверстий и пучка вид зависимости Si(
является функцией входной величины х. За маской устанавливаются либо фотоприемники, либо оптические элементы канализации света для передачи сигналов (при необходимости — после нормализации) на последующую обработку. Выходной функцией системы является площадь засветки ФП или входной апертуры оптической системы Si, где i - номер засвеченного oтверстия маски. При диаметре отверстий D = d, их шаге W =1,5D, постоянном расстоянии от ЭОД до маски, квадратных сечениях отверстий и пучка вид зависимости Si(![]() ), а следовательно, и Si(х), примет вид, показанный на рисунке 1.6,б.
), а следовательно, и Si(х), примет вид, показанный на рисунке 1.6,б.
Если принять входной сигнал описанной дефлекторной системы как «четкий» входной параметр х, то площадь засветки каждого отверстия маски Si, отнесенная к Smах, будет соответствовать величине А(х) для каждого i-го терма. Интерпретируя пример лингвистически, можно сказать, что если входной величиной х является температура, то засветка первого отверстия маски будет соответствовать значению температуры "низкая", второго — "средняя", и третьего - "высокая".
За рубежом работы в направлении разработок различных оптических методов и оптоэлектронных средств нечетко-логической обработки информации ведутся в ряде ведущих университетов США: City University of New York, The University of Tennessee, The University of Maiami, Northwestern University, Massachusetts Institute of Technology, University of Colorado и др., а также в Китае и Японии.
Разработки коммерческих продуктов в смежных областях (оптические логические процессоры и вентили, системы оптической памяти) ведут такие известные своими инновационными разработками фирмы, как Highland Technology, Physical Optics Corp., InPhase Technologies, Digital Optical Technologies, INTEL и др.
Рассмотрим основные достоинства и недостатки рассмотренных выше аппаратных средств нечетко-логических систем.
Основным достоинством реализаций нечетких процессоров на основе цифровых, цифро-аналоговых и микропроцессорных СБИС является достаточная гибкость проектирования при использовании в конкретных приложениях. Это обеспечивается наличием мощного комплекса инструментальных аппаратно-программных средств разработки нечетких регуляторов, наличием АРМ конструкторов нечетких регуляторов, которые позволяют построить логические регуляторы, основу которых составляют нечеткие процессоры па СБИС. Кроме того, микропроцессорные и цифровые СБИС обладают достаточным запасом надежности и стабильностью характеристик и параметров. Однако, описанные микропроцессорные реализации нечетких регуляторов не способны использовать в полной мере все потенциальные возможности нечеткой логики по следующим объективным причинам:
- их быстродействие ограничено в части реализации ряда сложных нечетких операторов из-за последовательной обработки данных, присущей современным микропроцессорным средствам;
- погрешность вычислений с течением времени постоянно растет из-за неизбежных методических ошибок, обусловленных использованием цифровых методов вычисления;
- в микропроцессорных системах обработки нечеткой информации с увеличением значений базовых шкал нечетких переменных происходит нелинейное увеличение времени выполнения операций над элементами термов этих переменных, а также этапов фаззификации и дефаззификации; увеличение значений базовых шкал нечетких множеств ведет к неизбежному увеличению областей памяти микропроцессорных реализаций для хранения и обработки данных, что ведет к увеличению времени выполнения вычислительных операций.
Так, например, специализированный вычислительный комплекс обработки нечеткой информации, выполненный на базе микропроцессорных средств [21], позволяет осуществить операцию выборки элемента терма лишь за 5 мкс, а реализацию одной микрокоманды только за 2 мкс. При реализации на ПЭВМ типа РС ХТ/АТ с типовым 16-разрядным процессором 8086 время, требуемое на обработку процесса нечеткого логического вывода из набора 96 продукционных правил (5 входных переменных и 2 выходные переменные) составило 30 с [67]. Очевидно, что для работы систем управления в реальном времени требуется значительно большее быстродействие.
Кроме того, существующие микропроцессорные системы обработки нечеткой информации обладают значительными габаритами, массой и потребляемой мощностью.
Распараллеливание вычислений в микропроцессорных аппаратных средствах требует введения аппаратной избыточности, что, в свою очередь, ставит проблемы синхронизации параллельных вычислительных потоков и увеличения мощности энергопотребления, а также массогабаритных характеристик системы в целом. Так, мультимикропроцессорная система, описанная в [8], имеет габаритные размеры 600x2200x1000 мм, массу порядка
В отношении разработанных оптических методов, реализующих вычисления в нечеткой логике, можно сказать, что использование в качестве переносчика информации оптического потока позволяет решить проблемы быстродействия и распараллеливания вычислений с достаточной точностью вычислений на произвольном интервале времени обработки информации. Но используемые на сегодняшний день методы, такие как методы Фурье-оптики и Фурье-голографии, достаточно трудно реализуемы и не позволяют обеспечить весь комплекс операций над нечеткими множествами и отношениями, а также не дают возможности реализовать нечетко-логический вывод в целом. Например, оптические методы, описанные в [26], позволяют реализовать только операции min-конъюнкции, mах-дизъюнкции, min-импликации, тавтологии и противоречия. Описанное в [1] оптоэлектронное логическое устройство использует классические принципы оптических методов обработки информации и интегральной оптики, обладает простотой конструкции, но реализует только комплекс параметризованных t-норм и t-конорм.
В отношении оптоэлектронного фаззификатора, описанного в [10] и показанного на рисунке 1.7 а), в качестве недостатка можно указать невозможность реализации произвольных функций принадлежности.
Таким образом, оказывается весьма актуальной проблема поиска новых методов, подходов и устройств при построении нечетких процессоров, позволяющих реализовать весь спектр операций нечеткой логики, причем, с быстродействием, обеспечивающим обработку входной информации практически в реальном масштабе времени, а также обладающих простотой конструкции и обеспечивающих высокую точность вычисления на произвольном интервале времени обработки информации.
Решению этой проблемы и посвящено дальнейшее изложение материала книги.
1. Аверкин, А.Н. и др. Нечеткие множества в моделях управления и искусственного интеллекта. - М.: Наука, 1986.
2. Акаев А.А., Майоров С.А. Оптические методы обработки информации.- М.: Высшая школа, 1988.
3. А.с. №1223259. СССР, 1986. Селектор минимального сигнала / Соколов С.В., Никулин Ю.Я., Огреб С.М.
4. А.с. №1767507. Россия, 1994. Оптический интегратор / Соколов С.В.
5. Бадеева Е.А., Гориш А.В., Котов А.Н., Мурашкина Т.И., Пивкин А.Г. Теоретические основы проектирования амплитудных волоконно-оптических датчиков давления с открытым оптическим каналом: М.:МГУЛ, 2004.- 246 с.
6. Борисов А.Н., Крумберг О.А., Федоров И.П. Принятие решений на основе нечетких моделей: Примеры использования.- Рига : Знание.1990.-184 с.
7. Бобровников, Л.З. Электроника. Учебник для вузов. 5-е изд. / Л.З. Бобровников. - СПб.: Изд-во «Питер», 2004. - 560 с.
8. Буравлёв, А. Масштабируемые мультипроцессорные вычислительные системы высокой производительности / А. Буравлёв, М. Чельдиев, А. Барыбин, В. Костенко, Д. Тумакин, Г. Петрова // Современные технологии автоматизации. - 2009. - № 3. - С. 72-76.
9. Ванюрихин А.И., Герчановская В.П. Оптико-электронные поляризационные устройства. - Киев: Техника, 1984.
10. Городецкий, А.Е. Нечеткие технологии управления в оптоэлектронных системах / Городецкий А. Е., Ерофеев А. А., Жуйков А. Ю. // Тез. докл. «Междунар. конф. по мягким вычислениям и измерениям» - СПб., 2000г.
11. Догу М. Обзор инструментальных средств на нечеткой логике // Дэнси Гидзюцу, 1991.-Т. 33. № 1.
12. Змитрович А.И. Интеллектуальные информационные системы.-Мн.:НТООО «ТетраСистемс», 1997.- 368 с.
13. Иванов, В.И. Полупроводниковые оптоэлектронные приборы: Справочник / В.И. Иванов, А.И. Аксенов, А.М. Юшин; Под ред. Н.Н Горюнова. - М.: Энергоатомиздат, 1984. -184 с.
14. Исихара С. Оптические компьютеры. Новый век науки. / Под ред. М.А.Воронцова. М.: Наука, 1992.
15. Клэр, Ж.-Ж. Введение в интегральную оптику: Пер. с франц. Под редакцией В.К. Соколова / Ж.-Ж. Клэр. - М.: Сов.радио, 1980. - 104 с.
16. Крамаров С.О., Соколов С.В. Оптические компьютеры в обучении: перспективы и реальность Материалы Всероссийских научно-практических конференций-выставок: «Информатизация образования 96 и 97», Ставрополь, изд. СГУ, 1997.
17. Либерман, Ф.Я. Электроника на железнодорожном транспорте: Учеб. пособие для вузов ж.-д. трансп. / Ф.Я. Либерман. - М: Транспорт, 1987. - 288 с.
18. Маккавеев, В. Фотонные коммутаторы/ В. Маккавеев // Компоненты и технологии. - 2006. - № 2. - С. 142-146.
19. Майоров С.А., Очин Е.Ф., Романов Ю.Ф. Оптические аналоговые вычислительные машины. - Л.: Энергоатомиздат, 1983.
20. Марше Ж. Операционные усилители и их применение. Пер. с франц. / Ж. Марше. -Л.: Издательство «Энергия», 1974. - 216 с.
21. Мелихов, А.Н. Проектирование микропроцессорных средств обработки нечеткой информации / А.Н Мелихов, В.Д. Баронец. - Ростов - н/Д: Издательство Ростовского университета, 1990. - 128 с.
22. Мировицкий Д.И., Будагян И.Ф., Дубровин В.Ф. Микроволноводная оптика и голография. - М.: Наука, 1983.
23. Носов, Ю.Р. Оптоэлектроника / Ю.Р. Носов. - М.: Радио и связь, 1989. - 360 с.
24. Оптические вычисления / Под ред. Р. Арратуна. - М.: Мир, 1993.
25. Оптическая обработка информации / Под ред. Д. Кейсесента. - М.: Мир, 1980.
26. Павлов, А.В. Обработка информации оптическими методами: в 2 т. - СПб.: СПбГУ ИТМО, 2010. - 78 с.
27. Патент № RU 2020528, Россия, 1994. Оптический триггер / Соколов С.В.
28. Патент № RU 2020551, Россия, 1994. Оптический компаратор / Соколов С.В.
29. Патент № RU 2040028, Россия, 1995. Оптический триггер / Соколов С.В.
30. Патент № RU 2159461, Россия, 2000. Оптический дифференциатор / С.В. Соколов, П.С. Шевчук, Р.Н. Ганеев, А.В. Момот.
31. Патент № RU 2408051, Россия, 2010. Оптоэлектронный дефаззификатор / Курейчик В.М., Курейчик В.В., М.А. Аллес, С.В. Соколов, С.М. Ковалев.
32. Патент № RU 2408052, Россия, 2010. Оптоэлектронный дефаззификатор / Курейчик В.М., Курейчик В.В., М.А. Аллес, С.В. Соколов, С.М. Ковалев.
33. Патент № RU 2409831, Россия, 2011. Оптический дефаззификатор / Курейчик В.М., Курейчик В.В., М.А. Аллес, С.В. Соколов, С.М. Ковалев.
34. Патент № RU 2416119, Россия, 2011. Оптический фаззификатор / Курейчик В.М., Курейчик В.В., М.А. Аллес, С.В. Соколов, С.М. Ковалев.
35. Патент № RU 2 419 127, Россия, 2011. Оптический дизъюнктор непрерывных множеств / Курейчик В.М., Курейчик В.В., М.А. Аллес, С.В. Соколов, С.М. Ковалев
36. Патент № RU 2 419 128, Россия, 2011. Оптический конъюнктор непрерывных множеств / Курейчик В.М., Курейчик В.В., М.А. Аллес, С.В. Соколов, С.М. Ковалев
37. Патент № RU 2 422 876, Россия, 2011. Оптический дизъюнктор непрерывных множеств / М.А. Аллес, С.В. Соколов, С.М. Ковалев
38. Патент № RU 2 429 519, Россия, 2011. Оптический вычислитель симметрической разности непрерывных множеств / М.А. Аллес, С.В. Соколов, С.М. Ковалев
39. Патент № RU 2 432 597, Россия, 2011. Оптический вычислитель функции по модулю числа / М.А. Аллес, С.В. Соколов, С.М. Ковалев
40. Патент № RU 2 432 598, Россия, 2011. Оптический граничный дизъюнктор нечетких множеств / М.А. Аллес, С.В. Соколов, С.М. Ковалев
41. Патент № RU 2 432 599, Россия, 2011. Оптический фаззификатор / М.А. Аллес, С.В. Соколов, С.М. Ковалев
42. Патент № RU 2 432 600, Россия, 2011. Оптический дизъюнктор непрерывных (нечетких) множеств / М.А. Аллес, С.В. Соколов, С.М. Ковалев
43. Патент № RU 2 432 602, Россия, 2011. Оптический граничный конъюнктор нечетких множеств / М.А. Аллес, С.В. Соколов, С.М. Ковалев
44. Патент № RU 2 432 670, Россия, 2011. Оптический генератор импульсных последовательностей / М.А. Аллес, С.В. Соколов
45. Патент № RU 2 433 446, Россия, 2011. Оптический вычислитель разности непрерывных множеств / М.А. Аллес, С.В. Соколов, С.М. Ковалев
46. Патент № RU 2 435 191, Россия, 2011. Оптический алгебраический объединитель нечетких множеств / М.А. Аллес, С.В. Соколов, С.М. Ковалев
47. Патент № RU 2 435 192, Россия, 2011. Оптический Д-конъюнктор нечетких множеств / М.А. Аллес, С.В. Соколов, С.М. Ковалев
48. Патент № RU 2 435 193, Россия, 2011. Оптический конъюнктор непрерывных (нечетких) множеств / М.А. Аллес, С.В. Соколов, С.М. Ковалев
49. Патент № RU 2 437 139, Россия, 2011. Оптический граничный дизъюнктор нечетких множеств / М.А. Аллес, С.В. Соколов, С.М. Ковалев
50. Патент № RU 2 439 651, Россия, 2012. Оптоэлектронный дефаззификатор / М.А. Аллес, С.В. Соколов, С.М. Ковалев
51. Патент № RU 2 439 652, Россия, 2012. Оптоэлектронный дефаззификатор / М.А. Аллес, С.В. Соколов, С.М. Ковалев
52. Патент № RU 2 441 267, Россия, 2012. Оптический вычислитель нечеткого включения нечетких множеств / М.А. Аллес, С.В. Соколов, С.М. Ковалев
53. Патент № RU 2 442 204, Россия, 2012. Оптический коммутатор / С.В. Соколов и др.
54. Патент № RU 2 444 036, Россия, 2012. Оптический коммутатор / С.В. Соколов и др.
55. Патент № RU 2 444 047, Россия, 2012. Оптический дефаззификатор / М.А. Аллес, С.В. Соколов, С.М. Ковалев
56. Патент № RU 2 445 672, Россия, 2012. Оптоэлектронный нечеткий процессор / М.А. Аллес, С.В. Соколов, С.М. Ковалев
57. Патент № RU 2 446 431, Россия, 2012. Оптический фаззификатор / М.А. Аллес, С.В. Соколов, С.М. Ковалев
58. Патент № RU 2 446 432, Россия, 2012. Оптоэлектронный дефаззификатор / М.А. Аллес, С.В. Соколов, С.М. Ковалев
59. Патент № RU 2 446 433, Россия, 2012. Оптоэлектронный нечеткий процессор / М.А. Аллес, С.В. Соколов, С.М. Ковалев
60. Патент № RU 2 446 434, Россия, 2012. Оптический фаззификатор / М.А. Аллес, С.В. Соколов, С.М. Ковалев
61. Патент № RU 2 446 435, Россия, 2012. Оптоэлектронный дефаззификатор / М.А. Аллес, С.В. Соколов, С.М. Ковалев
62. Патент № RU 2 446 436, Россия, 2012. Оптоэлектронный нечеткий процессор / М.А. Аллес, С.В. Соколов, С.М. Ковалев
63. Патент № RU 2 451 976, Россия, 2012. Оптический Д-дизъюнктор нечетких множеств / М.А. Аллес, С.В. Соколов, С.М. Ковалев
64. Патент № RU 2 458 377, Россия, 2012. Оптический JK-триггер / М.А. Аллес, С.В. Соколов
65. Патент № RU 2 461 031, Россия, 2012. Оптический Т-триггер / М.А. Аллес, С.В. Соколов
66. Патент № RU 2 463 640, Россия, 2012. Оптический вычислитель дополнения нечеткого множества / М.А. Аллес, С.В. Соколов, С.М. Ковалев
67. Пегат А. Нечеткое моделирование и управление. - М.: БИНОМ, 2009. - 798 с.
68. Применение методов Фурье-оптики. / Под ред. Старка Г. - М.: Радио и связь, 1988.
69. Свечников С.В. Элементы оптоэлектроники. - М.: Сов. радио, 1971.
70. Семенов А.С., Смирнов В.Л., Шмалько А.В. Интегральная оптика для систем передачи и обработки информации. - М.: Радио и связь, 1990. - 224 с.
71. Соколов С.В. О применении волноводной оптики для построения функциональных элементов оптических ЦВМ // Автометрия. 1992. № 4.
72. Соколов С.В. О построении волноводно-оптического двоичного умножителя для оптических ЦВМ // Автометрия. 1997. № 3.
73. Соколов С.В. Многофункциональное использование кольцевого оптического устройства // Известия Вузов. Приборостроение. 1991. № 1.
74. Соколов С.В. О синтезе пространственного оптического функционального преобразователя // Известия Вузов. Приборостроение. 1993. № 9 - 10.
75. Соколов С.В. Применение оптических волноводов для синтеза процессорных схем // Известия Вузов. Радиоэлектроника. 1995. № 2.
76. Соколов С.В. Некогерентное волноводно-оптическое устройство для решения дифференциальных уравнений //Известия Вузов. Радиоэлектроника. 1996. № 2.
77. Соколов С.В. Синтез функциональных элементов оптических компьютеров на основе связанных оптических волноводов // Известия Вузов. Радиоэлектроника. 1997. № 5.
78. Соколов С.В. Синтез оптических преобразователей информации // Оптический журнал. 1994. № 7.
79. Соколов С.В. О принципах синтеза некогерентных волноводно-оптических матричных процессоров // Оптический журнал. 1996. № 1.
80. Соколов С.В. Некогерентно-оптический матричный процессор // Оптический журнал. 1998. № 9.
81. Соколов С.В. Использование нелинейной и волноводной оптики при синтезе цифровых вычислителей // Оптический журнал. 1999. № 2.
82. Соколов С.В. Об одном принципе построения волоконно-оптических некогерентных вычислительных устройств // Радиотехника. 1993. № 8 - 9.
83. Соколов С.В. Некогерентно-оптические процессорные схемы // Радиотехника. 1997. № 8.
84. Справочник по теории автоматического управления / под ред. А.А. Красовского. - М.: Наука. Гл. ред. физ.-мат. лит., 1987. - 712 с.
85. Ульянов С.В. Нечеткие модели интеллектуальных промышленных систем управления: теоретические и прикладные аспекты // Изв. АН СССР. Техническая кибернетика, 1991. - № 3.
86. Фотоника / Под ред. М. Балкански, П. Лалемана. - М.: Мир, 1978.
87. Щерба, А. Программируемые аналоговые ИС Anadigm: применение конфигурируемых аналоговых модулей в составе программы Anadigm Designer2 / А. Щерба // Компоненты и технологии .- 2007. - №12.
88. Kramarov S.O., Sokolov S.V. Optical Spatially distributed computer - based information system // ISAF’ 96 PAPERS, part 2, NJ, USA, 1996.
89. Kramarov S.O., Sokolov S.V. Synthesis of functional units for optical computers based on the Spatial-spaced waveguide structures //8-th International Meeting on Ferroelectric-Semiconductors (IMFS-8), Rostov-on-Don,1998.
90. abc.vvsu.ru // Сайт цифровых учебно-методических материалов Центра Образования ВГУЭС.





