Воронеж, Воронежская область, Россия
Ростов-на-Дону, Ростовская область, Россия
ББК 308 Монтаж, эксплуатация, ремонт машин и промышленного оборудования
В данной статье рассматривается модель анализа многокритериальной задачи, позволяющая существенно снизить проблемы, возникающие при проектировании сложных технических систем в случаях, когда требуется существенно снизить размерность векторного критерия в случае его избыточности, или показать, что такое сокращение невозможно.
анализ, модель, критерий, проектирование, проблема, система
Введение
Многие задачи оптимального проектирование сложных технических систем имеют многокритериальную основу. Причем, в качестве критериев как правило, берутся технические характеристики системы, а стратегии (альтернативы) представляют собой варианты ее проектов, задаваемые в виде наборов значений конструктивных параметров. Поскольку многокритериальные задачи проектирования сложных систем имеют большую размерность пространства стратегий и значительного времени расчёта характеристик их решение становится довольно затруднительным.
Другая особенность заключается в необходимости повторного решения многокритериальных задач с теми же критериями, но изменёнными множествами стратегий в связи с возможными в ходе проектирования изменениями конструктивных и функциональных ограничений, определяющих техническую систему [1,2].
Постановка задачи
В многокритериальных задачах «качество» (или «полезность», «ценность», «эффективность» и т. п.) объектов оценивается с помощью критериев 
понимается функция, отображающая множество объектов Q в некоторое, содержащее не менее двух точек, подмножества 
числовой прямой 
. Это множество называют шкалой i-го критерия, а его элементы – шкальными оценками.
Критерии 
образуют векторный критерий 
, отображающий множество Q во множество 
векторов, компонентами которых являются шкальные оценки. В общем случае не для всякого вектора 
может существовать соответствующий объект 
, т. е. такой, что 
. Однако для анализа задачи и получения необходимой информации с целью её решения удобно оперировать векторами из 
, которые не обязательно соответствуют реальным объектам (т. е. из Q), но могут рассматриваться как характеристики некоторых гипотетических объектов. Такие векторы будем называть векторными оценками. Множество всех векторных оценок обозначим через Х, поскольку векторные комбинации шкальных оценок могут оказаться недопустимыми, так как содержащие их векторы будут лишены смысла наборами чисел, то включение 
, вообще говоря, строгое.
При решении задачи на основании полученной информации во множестве векторных оценок Х строятся бинарные отношения предпочтения и безразличия, которые затем наряду с дополнительными гипотезами и принципами (например, принципом наибольшего гарантированного результата, применяемым при наличии неопределённых факторов) используются для построения отношения предпочтения во множестве стратегий U и выделения оптимальной стратегии [2,3]. В дальнейшем отношения строгого предпочтения, безразличия, нестрогого предпочтения и несравнимости будут обозначаться соответственно буквами P, I, R и N, которые при необходимости будут снабжаться теми или иными индексами (верхними или нижними).
Для любых двух векторных оценок 
возможен один и только один из следующих случаев:
Модель анализа многокритериальной задачи
Время, затрачиваемое на решение многокритериальной задачи проектирования, значительно сокращается при уменьшении размерности векторного критерия. Поэтому вопрос уменьшения этой размерности представляется весьма важным. Примером критерия, который может быть несущественным на раннем этапе проектирования, является стоимость технической системы. В самом деле, предположим, что одновременное не уменьшение всех существенных характеристик технической системы приводит к соответствующему не уменьшению её стоимости. Тогда критерий стоимости может быть исключён из векторного критерия, поскольку это не приведёт к сокращению множества оптимальных по Парето стратегий [1,4]. В данной ситуации критерий стоимости целесообразнее использовать на следующем этапе выбора проекта системы из набора оптимальных по Парето проектов.
Задача векторной (или многокритериальной) оптимизации заключается в выборе стратегии x из множества X возможных стратегий при наличии векторного критерия:
.
Без потери общности предположим, что по каждому частному критерию 
желательно иметь возможно большее значение [2]. В качестве решения этой задачи обычно берётся одна из стратегий, принадлежащих множеству эффективных стратегий:
В многокритериальных задачах проектирования сложных технических систем [1] часто требуется построить конечное множество 
, удовлетворяющее следующему условию: для всякой стратегии 
должна найтись стратегия 
такая, что 
мало. В [1] 
строится как объединение решений двухэтапных лексикографических задач:
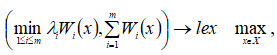
когда 
пробегает достаточно плотную конечную d-сеть множества 
. Трудоёмкость построения множества возрастает с увеличением размерности векторного критерия W. В данной работе исследуется вопрос уменьшения этой размерности путём исключения W несущественных качественных критериев.
Для непустого собственного подмножества S множества I={1, 2,…,m} положим 
. Пусть 
- множество эффективных стратегий из множества Х по векторному (или скалярному, если S – одноэлементно) критерию 
. Критерий 
назовём базисным, если 
. Если существует базисный критерий 
, то в рассмотренном выше лексикографическом критерии [1,3] в качестве первого критерия можно использовать 
, а d-сеть по 
брать из множества:
.
Критерий является базисным, если, например, из неравенства 
, всегда следует неравенство 
.
Рассмотрим вопрос проверки базисного критерия, и способы нахождения базисных критериев.
Утверждение 1. Для того, чтобы критерий был базисным, необходимо и достаточно, чтобы для любых стратегий 
.
Займёмся вопросом проверки базисности критерия . Если множество Х конечно, то эту проверку можно осуществить перебором, используя утверждение 1.
Теперь рассмотрим линейную задачу векторной оптимизации. Предположим, что Х – выпуклый многогранник евклидова пространства, а критерии 
линейны на Х. Пусть П – множество пар стратегий их множества 
эффективных по векторному критерию 
размерности 2m. Через 
обозначим множество пар 
, являющихся вершинами многогранника D. Положим
.
Утверждение 2. в линейной задаче векторной оптимизации для того, чтобы критерий был базисным, необходимо и достаточно, чтобы 
.
Необходимость. Предположим, что критерий является базисным, и 
. Тогда для некоторой стратегии 
. Заметим, что 
. В самом деле, если найдётся стратегия 
и 
).
Итак, 
и критерий не является базисным в силу утверждения 1.
Достаточность. Пусть . Предположим, что найдётся пара 
такая, что 
. Тогда 
и для некоторого конечного набора пар:
где 
.
Поскольку 
, найдётся номер 
такой, что 
. Следовательно, 
и 
(противоречие). Утверждение доказано.
Из утверждения 2 вытекает следующий способ проверки базисности критерия в линейной задачи векторной оптимизации. Сначала известными методами [1, 4] строится множество . Затем находится множество Q и для каждой стратегии 
осуществляется проверка её принадлежности множеству Р.
Пусть Х – компакт метрического пространства, а критерии 
непрерывны на Х. в этих условиях проверка базисности критерия может вызывать затруднения. Рассмотрим метод, который, хотя и не всегда, обеспечивает эту проверку, в практическом отношении может оказаться пригодным.
Пусть число 
мало, а - конечное подмножество множества Р, определённое в п.1. если для некоторой стратегии 
, то нельзя гарантировать базисность критерия . Но поскольку 
, можно считать критерий «
-базисным» и отбросить все критерии 
.
Алгоритм поиска базисного критерия
Алгоритм удобно разбить на m этапов.
Первый этап начинается с проверки базисности критерия 
. Предположим, что критерий не является базисным и нашлись стратегии 
такие, что 
. Если , где 
- базисный критерий, то необходимо 
.поэтому затем проверяется базисность критерия 
. Предположим, что нашлись стратегии 
, такие, что 
. Тогда проверяется базисность критерия , где 
, и т.д. до тех пор, пока не исчерпается множество 
. Если базисный критерий не обнаружен, то можно заключить, что ни один критерий 
, базисным не является. На этом завершается первый этап алгоритма.
Второй этап начинается с проверки базисности критерия 
и аналогичен первому этапу. Здесь только нужно учитывать, что критерий 
должен входить в базисный критерий. Точно также i-й этап алгоритма начинается с проверки базисного критерия 
и при этом критерии W1, …,Wi-1 входят в базисный критерий. В процессе выполнения всех m этапов алгоритма либо будет найден базисный («
-базисный») критерий, либо будет установлено отсутствие такого. При этом общее число проверок на базисность не превзойдёт 
.
Если нужно найти все базисные критерии (например, с целью отыскания базисного критерия наименьшей размерности), то необходимо пройти все m этапов алгоритма. В результате будет найдено некоторое множество 
базисных критериев. Далее нужно проверить на базисность критерии 
, вновь используя с небольшими изменениями предложенный алгоритм. В результате будет построено новое семейство базисных критериев. Процесс завершается построением всех базисных критериев.
Приведём утверждение, которое может оказаться полезным при поиске критериев.
Утверждение 3. Пусть - базисный критерий и для любых 
следует 
. Тогда при всех 
критерий 
является базисным.
Если - базисный критерий, но второе условие утверждения 3 не выполнено, то утверждение, вообще говоря, не имеет места.
Заключение
Таким образом, процесс поиска базисного критерия в задачах проектирования сложных систем является весьма трудоёмким. Он может оправдать себя в тех случаях, когда приходится большое число раз решать многокритериальные задачи с одним и тем же векторным критерием, но на разных множествах Х (например, при проектировании сложных технических систем [1]). В случаях, когда такой критерий удалось найти на достаточно «широком» множестве Х, то далее его можно использовать для построения сеток на множествах Парето для рассмотренного класса многокритериальных задач.
1. Цвиркун А. Д. Основы синтеза структуры сложных систем. М.: Наука, 1982. - 200 с.
2. Белоусов В.Е. Алгоритм для анализа вариантов решений в мно-гокритериальных задачах [Текст]/ Аксененко П.Ю., Белоусов В.Е., Кон-чаков С.А.// Системы управления и информационные технологии. №4(62), 2015. - С. 31-33.
3. Белоусов, В.Е. К проблеме решения задач многокритериальной оптимизации / В.Е. Белоусов, А.В. Гайдук, В.Н. Золоторев // Системы управления и информационные технологии. - 2006. - № 3(25). - С.34-43.
4. Белоусов В.Е., Лютова К.Г., Нгуен Вьет Туан. Модели квали-метрической оценки состояний сложных технических систем [Элек-тронный]// «Качество продукции: контроль, управление, повышение, планирование». Матер. Международная молодежная научно-практическая конференция. Курск (17-18 ноября 2015г): Издательство Юго-Западного государственного университета, Т.1, 2015. - C. 342-346.
