аспирант
Новочеркасск, Ростовская область, Россия
ГРНТИ 27.35 Математические модели естественных наук и технических наук. Уравнения математической физики
ГРНТИ 67.01 Общие вопросы строительства
ОКСО 01.04.03 Механика и математическое моделирование
ББК 221 Математика
ББК 308 Монтаж, эксплуатация, ремонт машин и промышленного оборудования
ТБК 6154 Математическое моделирование
В статье предлагается математическое моделирование растекания бурного потока в широком нижнем бьефе водопропускных сооружений в зависимости от расхода потока, относительного расширения нижнего бьефа и глубины воды на выходе из трубы круглого сечения. Рассматривается открытый водный поток в безнапорном режиме растекания. При числах Фруда, больших четырех в русле с относительным расширением b = 3 - 7 устанавливается сопряжение по типу свободного растекания двумерного бурного потока, определяются глубины и скорости потока в каждой точке, геометрия зоны свободного растекания. Параметры потока рассчитываются в любой точке зоны свободного растекания с помощью пакета прикладных программ Maple. Показана адекватность модельной крайней линии тока с экспериментальной.
Бурный поток, математическая модель, водопропускное сооружение, свободное растекание.
Надежность дорожных и мелиоративных трубчатых водопропускных сооружений во многом зависит от гидравлических условий работы их нижних бьефов, где возникают сложные пространственные формы сопряжения бурного потока.
Метод расчета заключается в сведении задачи к выбору эквивалентной ширины прямоугольной трубы. Задача определения параметров потока за прямоугольной трубой решена в работах [1,2,3]. Однако в практике строительства дорожных водопропускных сооружений применяются в основном трубы круглого сечения. Это доказывает актуальность настоящей работы. Актуальность работы также подтверждается и тем, что необходимо получить аналитические, удобные для пользователей зависимости по определению параметров потока в окрестности выхода потока из трубы с адекватностью реальному процессу, превышающей адекватность по имеющимся в настоящее время методикам [4,5,6]. В работах [1,2,3] показано, что решение задачи зависит от критерия Фруда 
на выходе потока из трубы, а именно: решение при 
отличается от решения при 
Определение глубины потока на его выходе из круглой трубы и эквивалентной ширины потока за прямоугольной трубой
При заданном расходе потока 
и выбранном диаметре трубы d согласно методике в справочной литературе по гидравлике [7] определяется параметр расхода для прямоугольных труб 
. Далее из графика зависимости [7] определяется глубина потока на выходе из трубы
Параметры 
являются исходными для решения задачи определения всего комплекса параметров потока за круглой трубой.
По величинам 
и d определим площадь живого сечения потока 
по формулам в [8] (см. рис. 1 а), б)). На рисунке 1 а) показано живое сечение потока в безнапорном режиме работы трубы при 
а на рис. 1 б) живое сечение потока в полунапорном режиме при 
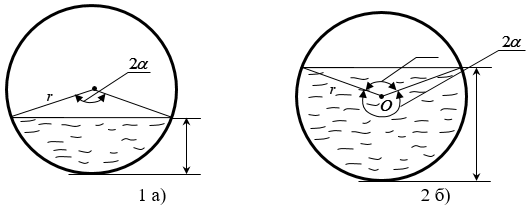
Рис. 1 Схема к определению площади живого сечения на его выходе из трубы
Для безнапорного режима течения
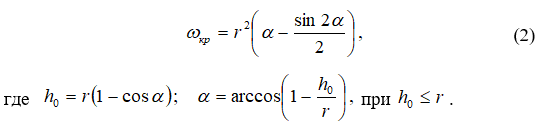
Для полунапорного режима течения
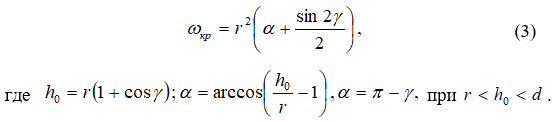
Эквивалентная ширина прямоугольной трубы определяется из условия совпадения площадей живых сечений на выходе потока из круглой и соответствующей прямоугольной труб:
Определение максимального угла растекания потока вдоль крайней верхней линии тока
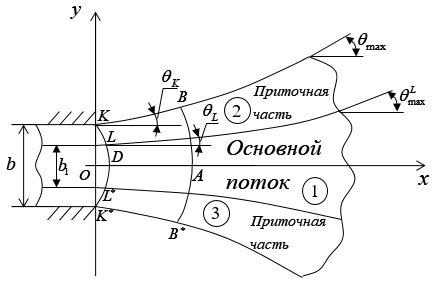
Рис. 2 План растекания потока за эквивалентной прямоугольной трубой.
эквивалентная ширина прямоугольной трубы всего потока;
ширина трубы основного потока;
Разделим, условно, живое сечение потока в круглой трубе на основное и приточное (см. рис. 2, 3)
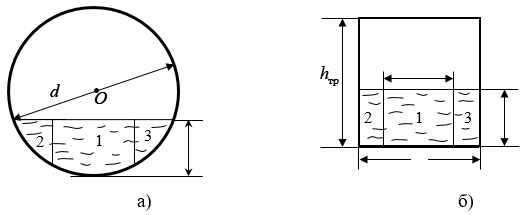
Рис. 3 Выделение в круглой трубе и соответственно в прямоугольной участков, формирующих основной поток и его приточную часть – 2, 3
Сечение 1 (рис. 3 а) формирует за круглой трубой основной поток. По форме сечение 1 мало отличается от прямоугольника. Сечения 2 и 3 формируют приточные части. Их особенность заключается в том, что они примыкают к основному сечению и возмущения, возникающие в них, распространяются в потоке независимо от основной его части. На рис. 3 б) показаны участки, соответствующие участкам на рис. 3 а).
Модуль скорости на выходе потока из трубы определим по формуле:
Тогда параметр кинетичности потока на его выходе из трубы :
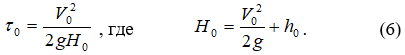
Рассматриваем случай, когда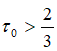 
и соответственно число Фруда 
. Максимальный угол растекания потока вдоль линии тока, ограничивающей основной поток, определим по методу, изложенному в работах [1,2,3]:
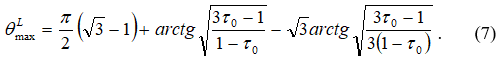
Далее определим параметры потока 
в точке 
. Согласно теории в работах [1,2,3] эти параметры определяются решением системы уравнений:
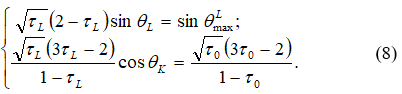
Решение системы уравнений (8) сводится к решению следующего уравнения пятой степени [9]:
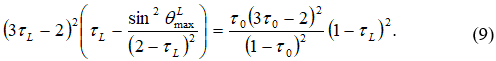
Уравнение (9) имеет единственное решение при 
. Решается это уравнение численно с использованием пакетов прикладных программ Maple или Mathcad.
Острый угол 
определяется выражением
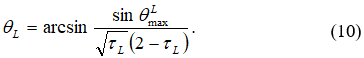
Максимальный угол растекания всего потока вдоль крайней верхней линии тока (рис. 2) определим из уравнения эпициклоиды, проходящей через точки 
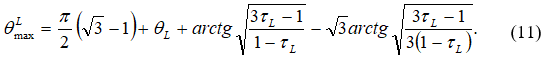
Определение параметров потока в точке 
(рис. 2)
Параметры потока в точке 
определяются решением следующей системы уравнений:
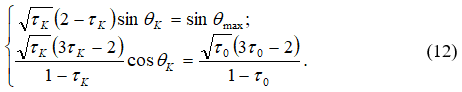
Решение системы (12) сводится к решению уравнения относительно 
аналогично уравнению (9). После нахождения корня 
угол 
определяется по формуле
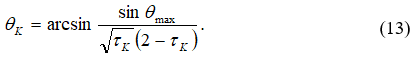
Далее при расчете параметров потока за эквивалентной прямоугольной трубой необходимо использовать результаты решения задачи, приведенные в работе [9]. В настоящей работе приведем метод определения параметров потока 
в точках крайней верхней линии тока и в точках на оси симметрии потока, а также метод определения координат этих точек (рис. 4)
Определение параметров потока 
на крайней линии тока
Параметры потока 
вдоль крайней линии тока удовлетворяют следующей системе уравнений (рис. 4):
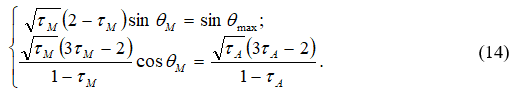
где 
значение параметра 
в точке 
, через которую проходит эквипотенциаль 
.
Значение 
задается глубиной потока в точке :
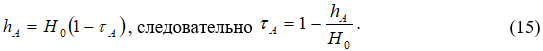
Метод решения системы (14) аналогичен методу решения системы (12).
Рис. 4 План растекания потока
KM крайняя линия тока;
AM произвольная эквипотенциаль, проходящая через точки A и M
Определение координат точек A и M, в которых известны параметры 
Из содержания работы [9] известно, что справедлива следующая дифференциальная связь между дифференциалами dx,dy, дифференциалом 
и параметром 
вдоль крайней линии тока:
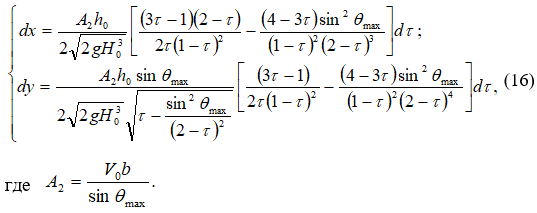
Вдоль оси симметрии потока справедлива дифференциальная связь
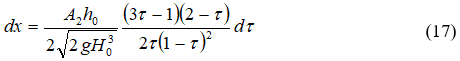
Интегрированием системы (16) найдем координаты точки M:
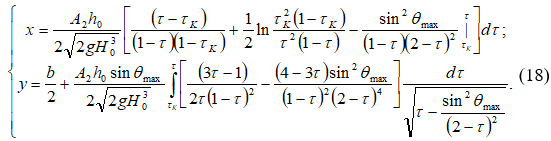
Интегрируя уравнение (17), получим абсциссу точки A на оси потока
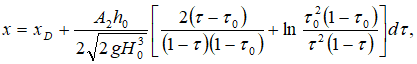
где 
определяется по формулам, приведенным в работах [1,2,3,8].
Вычисление интеграла в правой части выражения для 
в (18)
Так как вдоль крайней верхней линии тока
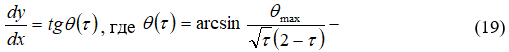
острый угол, то методы численного интегрирования для определения 
во втором уравнении из (20) даны в [10]. Пусть
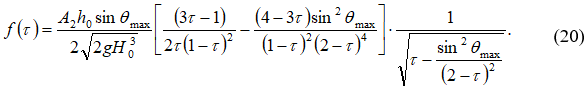
Интегрируя второе уравнение системы (16), получим
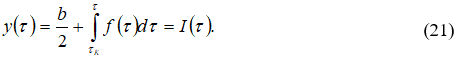
Для вычисления интеграла 
воспользуемся последовательно формулами:
правило трапеций;
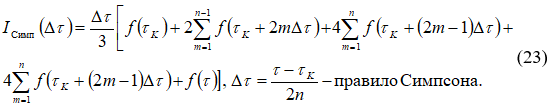
Вычисления проводились с относительной погрешностью 
В результате было установлено, что для вычисления интеграла (21) с заданной погрешностью можно пользоваться формулой Симпсона с шагом 
, или меньшим. Погрешность вычисления интеграла определялась по правилу Рунге – Ромберга [11]
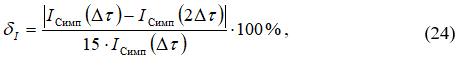
где 
- значение интеграла, вычисленное по формуле Симпсона с шагом 
;
- значение интеграла, вычисленное с двойным шагом.
Сравнение формы (геометрии) крайних линий тока:
модельных и экспериментальных
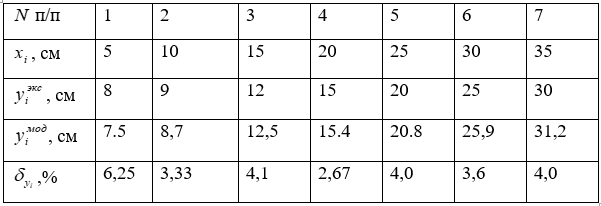
Результаты экспериментов взяты из работы [12]. Исходные данные для определения модельных и экспериментальных значений ординат 
.
1). Диаметр трубы 
2). Максимальная глубина потока на выходе из трубы 
3). Скорость потока на выходе из трубы 
.
Таблица 1
Координаты крайней линии тока свободно растекающегося потока и рассогласование с экспериментом
Выводы по работе
1. Метод аналитического определения параметров свободно растекающегося водного потока в окрестности его выхода из круглой трубы оправдан логически и подтверждается высокой степенью сходимости по параметрам потока: реального и модельного.
2. Численные методы расчета интегралов в работе с использованием правила Симпсона и оценки погрешности результатов модели и экспериментов показывают приемлемость методов.
1. Коханенко В.Н. Моделирование одномерных и двухмерных открытых водных потоков [Текст]: монография / В.Н. Коханенко, Я.В. Волосухин, В.В. Ширяев, Н.В. Коханенко. - Ростов н/Д: Изд-во ЮФУ, 2007. - 168 с.
2. Коханенко В.Н. Моделирование бурных двухмерных в плане водных потоков [Текст]: монография / В.Н. Коханенко, Я.В. Волосухин, М.А. Лемешко, Н.Г. Папченко. - Ростов н/Д: Изд-во ЮФУ, 2013. - 180 с.
3. Ширяев В.В. Развитие теории двухмерных открытых водных потоков [Текст]: монография / В.В. Ширяев, М.Ф. Мицик, Е.В. Дуванская; под общ. ред. В.В. Ширяева. - Шахты: Изд-во ЮРГУЭС, 2007. - 133 с.
4. Шеренков И.А. О плановой задаче растекания струи бурного потока несжимаемой жидкости [Текст] / И.А. Шеренков // Известия АН СССР. ОТН. - 1958. - № 1. - С. 72-78.
5. Лилицкий Г.А. Исследования растекания бурного потока в нижнем бьефе водопропускных сооружений [Текст] / Г.А. Лилицкий // Гидравлика и гидротехника: Респ. межвед. научно-техн. сб. - Киев: Техника, 1966. - Вып. 2. - С. 78-84.
6. Мищук Г.Я. Определение поля скоростей в плане растекащегося бурного потока методом характеристик [Текст] / Г.Я. Мищук // Известия вузов. Энергетика. - Минск. - 1963. - № 10.
7. Справочник по гидравлике [Текст] / Под ред. В.А. Большакова. - 2-е изд., перераб. и доп. - Киев: Вища школа, 1984. - 343 с.
8. Корн Г. Справочник по математике для научных работников и инженеров [Текст] / Г. Корн, Т. Корн. - М.: Наука, 1970. - 720 с.
9. Мицик М.Ф. Метод с использованием годографа скорости применительно к расчету параметров бурного двухмерного потока [Текст] / М.Ф. Мицик, Н.В. Косиченко, М.А. Лемешко // Математическое и компьютерное моделирование естественнонаучных и социальных проблем: сб. ст. IV Междунар. научн.-техн. конф. молодых специалистов, аспирантов и студентов. - Пенза: Приволжский Дом знаний, 2010. - С. 130-141.
10. Самарский А.А. Численные методы [Текст]: учеб. пособие для вузов / А.А. Самарский, А.В. Гулин. - М.: Наука, 1989. - 432 с.
11. Березин И.С. Методы вычислений [Текст] / И.С. Березин, Н.П. Жидков. - М.: Изд-во ГИФМЛ, 1959. - Т. 1. - 620 с.
12. Кольченко О.Л. Управление кинематической структурой двухмерного бурного потока за трубчатыми водосбросными сооружениями [Текст]: автореф. дис. … канд. техн. наук: 05.14.09 / О.Л. Кольченко. - Киев, 1987. - 20 с.
