from 01.01.1977 to 01.01.2023
Rostov-on-Don, Rostov-on-Don, Russian Federation
Rostov na Donu, Rostov-on-Don, Russian Federation
Rostov-na-Donu, Rostov-on-Don, Russian Federation
Uneven deformations of the base occur even during the construction of the building. They may increase during the life cycle. The very process of developing norms and methods indicates that the existing experience and scientific base are finite. Therefore, the scientific base does not allow us to fully take into account some of the impacts and features of the design. The operational reliability of buildings exposed to excessive precipitation and rolls can be restored by eliminating excessive rolls. The methods of eliminating sediments and rolls can be divided into two groups. The first uses the processes of local weakening of the base in those fragments of the building in the plan where additional precipitation is required so that the total precipitation approaches a uniform one. The following methods are used here: partial soaking of the base, installation of pits (including horizontal ones under the foundation), and transfer of additional loads to the base. The main disadvantage of this group of methods for eliminating uneven precipitation is the low accuracy of preliminary numerical modeling of a number of processes. The second group of measures provides for leveling the building by lifting it with a system of jacks. In this method, the sagging part of the building is lifted relative to the foundation. The article discusses the main steps in levelling a building by lifting. The main tasks of structural mechanic an methods of their solution are described, which will ensure the reliability of the structure at different stages of alignment.
physical nonlinearity, cracking, normal stress, tangential stress, deformation components, strength theory, rolls, fracture, alignment
Введение
В процессе эксплуатации основания многоэтажных зданий получают неравномерные осадки. Под их влиянием здания подвергнуты неравномерным деформациям, как прогибы, крены и скручивание [1-4].
В рассматриваемой проблеме важен не сам факт неравномерных осадок основания, а то, какие опасные для эксплуатации деформации возникают в самом здании. Так как при этом существенно снижается эксплуатационная надежность объектов строительства. Наиболее распространенными являются: образование магистральных или локальных разрушений во фрагментах здания и крены. Крены влияют не только на снижение прочности самого объекта, но и приводят к нарушению нормальных условий эксплуатации инженерных систем.
Обзор свидетельствует о том, что на территории России и за рубежом, имеется множество зданий и сооружений, испытывающих значительные неравномерные деформации. Одним из методов восстановления эксплуатационной надежности является подъемом просевшей части здания системой домкратов. Основными причинами кренов здания является неверный учет работы основания. Например, неравномерные осадки грунтового основания, оползневые процессы и т.п. Так, в ФРГ в земле Саарлэнд основная причина значительных неравномерных осадок – шахтные подработки. На Юге РФ одной из основных причин – просадочные грунты и оползневые процессы на склонах [5-8] (рис. 1).
Возникновение сверхнормативных неравномерных деформаций зависит от множества объективных и субъективных факторов, связанных и с ошибками в процессе проектирования или изыскательских работ, различные ошибки при возведении или эксплуатации здания, в том числе влияние вновь возводимых рядом сооружений. Также важно то, что всегда существует некое ограничение в объеме накопленных научных и практических знаний и имеющегося опыта. Постоянно совершенствуются методы изысканий и расчетов, нормативные документы, конструктивные схемы зданий и проектные решения. Сам процесс развития норм и методов свидетельствует о том, что существующий опыт и научная база конечны. Поэтому научная база не позволяет в полной мере учесть некоторые воздействия и особенности работы конструкции. Например, ряд особенностей конкретного здания и участка строительства ранее практически не проявлялись в значительном влиянии на сооружения. Однако применительно к конкретному новому зданию определенные факторы могут оказать существенное влияние либо непосредственно, либо опосредованно [5-6, 9], могут сыграть роль «спускового крючка» для развития иных известных негативных процессов. В результате реальная и прогнозируемая эволюция работы сооружения могут существенно отличаться.
Одним из методов, хорошо зарекомендовавшим в практике выравнивания зданий, является неравномерный подъем системой домкратов, установленных между фундаментом и цоколем здания. Вторая группа мероприятий предусматривает выравнивание здания его подъемом системой домкратов [1-2]. Подобные работы выполняются, например, научно-производственной фирмой «Интербиотех» (Ростов-на-Дону). Выравнивание осуществляется системой плоских электрогидравлических домкратов [3]. В этом методе осуществляется подъем просевшей части здания относительно фундамента.
Работы при подъёме можно кратко представить так. По периметру несущих стен между фундаментом и зданием устраиваются домкратные ниши, в которых монтируются плоские домкраты и дополнительные подкрепляющие и распределяющие элементы; вместе с домкратными нишами они образуют так называемый «домкратный узел». Домкраты передают усилия на несущие конструкции непосредственно и через вспомогательный пояс жесткости, который крепится к стенам системой анкеров.
Можно выделить несколько этапов выравнивания кренов подъемом домкратами. Одним из наиболее ответственных является первый этап, при котором на домкраты подают максимальные усилия для преодоления связей между зданием и фундаментом. Для проектирования усиления цокольной и верхней части сооружения требуется выполнить механико-математическое моделирование процесса образования линии отрыва при увеличении усилий в домкратах. Для этого требуется использовать физически нелинейную постановку задачи [10-12]. Причем следует применять уточненные физические зависимости для тонкого слоя, в котором имеется адгезия между верхним строением и фундаментом.
На втором этапе осуществляется подъем здания на некоторую рабочую величину. Здесь связи между зданием и фундаментом разорваны, осуществляются только через точечно расставленные домкраты. Поэтому здание работает существенно отлично от проектного состояния, и необходимо рассматривать достаточность и прочность распределительных устройств и прочность их связей со зданием.
После чего начинается третий этап – поворот здания в вертикальных плоскостях. На этом этапе передается разная нагрузка на отдельные домкратные узлы для создания необходимого для поворота момента. В этом процессе также рассматриваются вопросы прочности несущих конструкций здания и распределительного усиления, но учитываются существенно различные усилия в группах домкратах.
После устранения кренов и восстановления связей с фундаментом начинается новый этап жизненного цикла здания. Неравномерные деформации основания могут развиваться и далее. Поэтому необходимо моделировать поведение системы во времени, чтобы предсказать дальнейшее поведение объекта, время эксплуатации до достижения предельных неравномерных деформаций.
На рис. 2 показана примерная схема устройства домкратных ниш и усиления.
На первом этапе на домкраты подают наибольшие усилия для преодоления связей между зданием и фундаментом – рис. 3. Здесь одним из ответственных моментов является этап начального отрыва несущих конструкций здания от фундамента. При этом наблюдается максимальные усилия в домкратах, превышающие усилия после отрыва (в процессе устранения крена здания) до 40%. Это объясняется двумя факторами – необходимостью преодоления адгезии между стеновыми панелями и фундаментом и необходимостью обеспечения, определенного линейного и углового ускорения для достижения определенных скоростей подъема. Опыт выравнивания зданий показал, что основной вклад в увеличение начальных усилий вносит адгезия.

Рис. 1. Примеры кренов зданий от неравномерных осадок и оползневых процессов
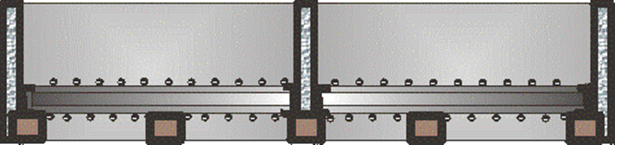
Рис. 2. Принципиальная схема расстановки домкратных ниш, домкратов и элементов усиления

Рис. 3. Варианты устройства усиления и домкратных узлов
Постановка задачи. Описание проблемы
Отрыв здания от фундамента характеризуется непрерывным изменением расчетной схемы за счет постепенного выключения из работы отдельных связей между несущими цокольными конструкциями и фундаментом (рис. 4). При этом цокольные конструкции ослаблены технологическими домкратными нишами. Как правило, в железобетонных цокольных панелях разрезается нижняя несущая арматура. Таким образом, здание работает по нехарактерной для него схеме с нарушенными несущими конструкциями и постепенным (достаточно быстрым) изменением условий опирания (от сплошного до дискретного на домкратах).
Для проектирования усиления цокольной и верхней части сооружения требуется выполнить механико-математическое моделирование процесса образования линии отрыва при увеличении усилий в домкратах. Для этого требуется использовать физически нелинейную постановку задачи. Причем следует применять уточненные физические зависимости для тонкого слоя, в котором имеется адгезия между верхним строением и фундаментом.

Рис. 4. Образование линии отрыва и ее развитие
Методика расчета и основные требования к модели
Важной задачей современной строительной механики является разработка уточненных методов расчета сооружений на деформируемых основаниях. Использование уточненных механико-математических моделей позволит не только получить более достоверные результаты работы системы «сооружение – фундамент – деформируемое основание», но и корректно решить инженерную проблему проектирования усиления и процесса выравнивания.
Разработка качественной механико-математической модели, описывающей работу различных объектов, невозможной без учета различных типов нелинейности. С.П. Тимошенко дополнительно предложил рассматривать конструктивную нелинейность [9, 13]. В частности, необходимость учета физической, геометрической и конструктивной нелинейности возникает при моделировании систем, которые подвержены изменению расчетной схемы сооружения на разных этапах эволюции.
Многочисленные экспериментальные исследования показали, что даже при малых перемещениях в поведении грунтового основания зависимости между напряжениями и деформациями имеют отклонения от линейной зависимости. Такого рода нелинейности при описании математических моделей поведения грунтовой среды учитываются нелинейной зависимостью между напряжениями и деформациями σ~ ε.
В процессе выравнивания здания, при увеличении нагрузки на домкраты, отдельные участки в адгезионном слое, или в окрестности последнего, достигают предельного состояния. Нарушаются внутренние связи, вследствие чего увеличиваются взаимные перемещения между фундаментом и стенами здания. При построении модели требуется выполнить учет больших взаимных перемещений, описать достижение предельного равновесия материала в отдельных зонах и учесть изменение расчетной схемы вследствие конечного взаимного смещения фрагментов.
Гипотезы наступления предельного состояния в некотором малом объёме материала достаточно развиты, однако актуальным остается вопрос моделирования поведения объёма при дальнейшем росте деформаций. Одной из постановок является учет образования трещин в процессе деформации расчетной области [10-12].
Выделение общих связей между напряжениями и деформациями в физически нелинейном материале с трещинами представляет собой сложную задачу. Появление трещин в процессе нагружения сооружения связано с разрушением материала, поэтому для получения приближенных зависимостей ϭ~ε необходимо привлекать подходящую теорию прочности.
Будем предполагать, что в материале существуют или могут возникнуть в процессе нагружения сооружения микротрещины, которые в состоянии близком к разрушению объединяются и формируют микротрещины. Таким образом, условно выделены два уровня рассмотрения состояния материала: с микро- и макротрещинами. В обоих случаях предполагается, что деформация есть осреднённая характеристика и определяется некоторыми средним значением по объему. Наличие микротрещин в материале учитывается прочностными характеристиками
Область прочного сопротивления материала находится внутри предельной поверхности:
$$τ \leq f(σ_{okm}μ_σ) $$ (1)
$$\left|\frac{dτ_{okm}}{dσ_{okm}}\right|< \sqrt{\frac{2(3+μ^2σ}{3-μ^σ}}$$ (2)
σokm(τokm) — нормальное (касательное) октаэдрическое напряжение;
μσ — параметр Надаи-Лоде для напряжений.
Как показано в [13], имеется возможность определить характер разрушения. Для хрупко-пластичных материалов характерны два вида разрушения: от отрыва и от сдвига по опасным поверхностям скольжения (1). Линейная аппроксимация предельной зависимости (1) позволила выделить Филоненко-Бородичу М.М. начало разрушения от сдвига (2), и при отрыве (2) разрушается.
Физические зависимости определим в соответствие с принятыми гипотезами об образовании трещин. Для пространственной задачи в точках среды при разрушении от отрыва могут возникнуть следующие ситуации.
1.Пусть в окрестности некоторой точки произошло разрушение от отрыва. Первая появившаяся трещина расположена на площадке, перпендикулярной к наибольшему главному напряжению σ1. После образования трещины материал в окрестности рассматриваемой точки перестанет работать на растяжение по направлению первой главной оси, т.е. можно положить
$$\left\{ \begin{matrix}
o \\
\sigma_2 \\
\sigma_3
\end{matrix} \right\}= \left[ \begin{matrix}
k+4/3g & k-2/3g & k-2/3g \\
k-2/3g & k+4/3g & k-2/3g\\
k-2/3g & k-2/3g & k+4/3g
\end{matrix} \right] \left\{
\begin{matrix}
\varepsilon_1 \\
\varepsilon_2 \\
\varepsilon_3
\end{matrix} \right\}$$ (3)
$$\varepsilon_1 =-\frac{3k-2G}{3k+1G}(\varepsilon_2+\varepsilon_3)$$ (4)
Подставим (4) в (3), получим:
$$\left\{ \begin{matrix}
\sigma_2 \\
\sigma_3
\end{matrix} \right\}= \left[ \begin{matrix}
\frac{4g(3k+g)}{3k+4g} & \frac{2g+(3k-2g)}{3k+4g} \\
\frac{2g+(3k-2g)}{3k+4g} & \frac{4g(3k+g)}{3k+4g}
\end{matrix} \right] \left\{
\begin{matrix}
\varepsilon_2 \\
\varepsilon_3
\end{matrix} \right\}$$ (5)
$$\sigma=D_{01}\varepsilon$$
2. Две пересекающиеся трещины при разрушении от отрыва могут появиться либо одновременно, если σ1=σ2>σ3 либо последовательно, если σ1>σ2=0>σ3 или σ1>σ2>σ3=0. В этом случае материал в окрестности рассматриваемой точки работает только по одной из главных осей, физические зависимости на главных осях имеют вид (6) и (7):
$$\varepsilon_1=\varepsilon_2=-\frac{3k-G}{2(3k+g)}\varepsilon_3$$ (6)
Исключая 𝝴1 и 𝝴2 из уравнения (6), получим:
$$\delta_3=\frac{9kg}{3k+g}\varepsilon_3$$ (7)
3. Для трех взаимно перпендикулярных пересекающихся трещин при отрыве все главные напряжения полагаются равными нулю, и физические зависимости принимаются в виде:
$$\sigma_j=o \cdot \varepsilon_j$$ (8)
где σjτ={σ1σ2σ3}; εjτ={ε1ε2ε3}.
Связь между напряжениями и деформациями, определенная в главных осях для среды с трещинами формулами (5-8), может быть записана в произвольной декартовой системе координат x, y, z, с помощью известных формул преобразования.
$$L=\left\{
\begin{matrix}
L_1 \\
L_2 \\
L_3
\end{matrix}
\right\}=
\left[\left[
\begin{matrix}
L_1^2 & L_2^2 & L_3^2 & L_1L_3 & L_1L_3 & L_2L_3 \\
M_1^2 & M_2^2 & M_3^2 & M_1M_3 & M_1M_3 & M_2M_3 \\
N_1^2 & N_2^2 & N_3^2 & N_1N_3 & N_1N_3 & N_2N_3
\end{matrix}
\right]\right]$$ (9)
Принимая во внимание (9), зависимости (5), (7), (8) записываются в следующем виде:
$$\left\{ \begin{matrix}
\sigma_X \\
\sigma_Y \\
\sigma_Z \\
\tau_xy \\
\tau_xz \\
\tau_yz \\
\end{matrix}
\right\}=
\left[
\begin{matrix}
B_{11}^k & B_{12}^k & B_{13}^k & B_{14}^k & B_{15}^k & B_{16}^k \\
& B_{22}^k & B_{23}^k & B_{24}^k & B_{25}^k & B_{26}^k \\
& & B_{33}^k & B_{34}^k & B_{35}^k & B_{36}^k \\
& & & B_{44}^k & B_{45}^k & B_{46}^k \\
& & & & B_{55}^k & B_{56}^k \\
& & & & & B_{66}^k
\end{matrix}
\right]
\left\{
\begin{matrix}
\varepsilon_X \\
\varepsilon_Y \\
\varepsilon_Z \\
\varepsilon_xy \\
\varepsilon_xz \\
\varepsilon_yz \\
\end{matrix}
\right\}$$
или σ=Bkε
(10)
Элементы матрицы В зависят от количества трещин, проходящих через точку среды: К=1, К=2 или К=3 (в данной статье варианты значений элементов В не приведены).
При разрушении от сдвига равно возможно появление в окрестности точки двух не ортогональных трещин, возникающих по площадкам, которые проходят через ось среднего по величине главного напряжения. В этом случае полагаем, что скольжение происходит по идеально гладкой поверхности и поэтому после выявления подобного типа разрушения полагаем σ1=σ2=0 и физический закон принимается в форме (10) при K=2.
Итак, при деформировании сооружения с учетом разрушения выше были выделены четыре типа напряженных состояний. Охарактеризовать их можно следующим образом. Первый тип, материал не разрушается, в окрестности точки возникает трехосное напряженное состояние. Второй тип, материал в окрестности точки имеет одну трещину- двухосное напряженное состояние. Третий тип, материал разрушился от отрыва или сдвига, в окрестности точки имеются две пересекающиеся трещины- одноосное напряженное состояние. Для четвертого типа в окрестности точки наступает полное исчерпание несущей способности материала, полное разрушение.
Из трехосного напряженного состояния I, могут возникнуть двухосное или одноосное напряженное состояние путем разрушения материала от отрыва или сдвига. Из состояния II можем возникнуть состояние III от отрыва и состояние IV при разрушении от сдвига. Из состояния III при любом характере разрушения возникает состояние IV, соответствующие полностью разрушенному материалу в окрестности точки.
Отметим, что полученные приближенные физические зависимости для материала с трещинами имеют анизотропный характер. Причем направление оси анизотропии зависит от положения главных осей и поэтому меняется от точки к точке.
Этот критерий использован в зависимостях для моделирования отрыва здания от фундаментов. Предлагается шаговый алгоритм (11), учитывающий переход на каждой итерации образования разрыва в новой точке среды или по новому направлению [5, 9, 11-12]:
$$\begin{cases}
K_K^1 \Delta \bar{q}^{(2)}=\Delta \bar{P}, или K_K^1 \Delta \bar{q}^{(2)}=P^{(1)}+\Delta \bar{P}-K_c^{(1)}q^{(1)} \\
\Delta \bar{\varepsilon}^{(2)}=\Phi \bar{q}^{(2)}, \Delta \bar{\sigma}^{(2)}=H^{(1)}\Delta \bar{\varepsilon}^{(2)} \end{cases}$$
$$\begin{cases}
\sigma^{(2)}_{i,r}=\sigma^{(1)}_{i,r}+\beta^{(2)}_r \Delta \bar{\sigma}^{(2)}_{i,r}=\sigma_{T,r},r=1..e \\
\beta^{(2)}=min\underset{(r)}{\{}\beta^{(2)}_r\}
\end{cases}$$
$$\begin{cases}
\varepsilon^{(2)}=\varepsilon^{(1)}+\beta^{(2)} \Delta \bar{\varepsilon}^{(2)}, \sigma^{(2)}=\sigma^{(1)}+\beta^{(2)} \Delta \bar{\sigma}^{(2)}
\end{cases}$$
(11)
На этапе дальнейшего прогнозирования поведения здания предлагается использовать пространственную модель ползучести, основанную на нелинейной теории наследственности Ю.Н. Работнова.
Для многоосного состояния известны прямая и альтернативная формулировка проблемы нелинейной ползучести (12).
$$\begin{cases}
\text{ПРЯМАЯ ФОРМА:} \\
\text{Уравнение ползучести: } \phi(\varepsilon)=\tilde{\sigma}=(1+L_1^*)\sigma=\sigma+\int\limits_0^t L_1(t-\theta)\sigma (\theta)d\theta \\
\text{или } \varepsilon=f[(1+L_1^*)\sigma]=f(\tilde{\sigma}) \\
\text{Уравнение релаксации: } \sigma=(1-R^*_1) \phi (\varepsilon)=\phi (\varepsilon)-\int\limits_0^t R_1(t-\theta)\phi (\varepsilon(\theta))d\theta \\
\text{АЛЬТЕРНАТИВНАЯ ФОРМА:} \\
\text{Уравнение ползучести: } \varepsilon=(1-L^*_2)f(\sigma)=f(\sigma)+\int\limits_0^t L_2(t-\theta)f(\sigma(\theta))d\theta \\
\text{Уравнение релаксации: } f(\sigma)=\hat{\varepsilon}=(1-R^*_2)\varepsilon=\varepsilon-\int\limits_0^t R_2(t-\theta)\varepsilon(\theta)d\theta \\
\text{или } \sigma=\phi [(1-R^*_2)\varepsilon]=\phi(\tilde{\varepsilon})
\end{cases} $$
(12)
При этом основные ядра ползучести и релаксации, входящие в (12), можно определить в экспериментах согласно (13-14):
$$L_1=\frac{E_K}{\sigma}\dot{\varepsilon}, L_2=\frac{E_C}{\sigma}\dot{\varepsilon}$$
(13)
$$R_1=\frac{1}{E_{C^\varepsilon}}\dot{\sigma}, R_1=\frac{1}{E_{K^\varepsilon}}\dot{\sigma}$$
(14)
Динамические эффекты, которые могут возникнуть при быстром развитии трещины или зон разрушения, следует оценивать, используя явные безусловно устойчивые схемы прямого интегрирования проф. Л.Н. Панасюка (13), обладающие малой трудоемкостью [14-16]:
$$\begin{cases}
(2M+ΔtC_D+0.5λΔt^2K_D)q^{n+1}=(2M+ΔtC_D+0.5λΔt^2K_D-Δt^2K)q^n+ \\
(2M+ΔtC_D-ΔtC+0.5λΔt^2K_D-0.5Δt^2K)s^n+0.5Δt^2(P^n+P^{n+1}, \\
s^{n+1}=-s^n+2(q^{n+1}-q^n),s=\dot{q}Δt,\dot{q}=^{dq}/_{dt},
\end{cases}$$
$$λ=max(eigen(K_D^{-1}K))$$
(13)
Обсуждение результатов

Рис. 5. Примеры напряженно-деформированного состояния
фрагмента здания, вертикальные напряжения
а) изменение НДС с учетом фактического крена здания;
б) опирание на систему домкратов;
в) опирание на систему расклинки

Рис. 6. Пример поэтапного образования линии отрыва
и зон разрушения в стенах на этапе подъёма здания (фрагмент)
без учета работы усиления

Рис. 7. Напряжения в шпильке крепления усиления и в ее окрестности
На рис. 5 показано изменение напряженного состояния в процессе выравнивания здания. Рассмотрено опирание на домкраты при полной и частичной передаче нагрузки, а также промежуточное опирание здания на систему «расклинки» при пере монтаже домкратов.
На рис. 6 показан пример использования программного комплекса ПОЛЮС при моделировании процесса выравнивания здания. Рассмотрен начальный вариант модели, в котором не учитывалось усиление стен. Показан фрагмент стены на одном из этапов увеличения нагрузки на домкраты (60% усилия). Отчетливо видно образование линии отрыва по нижнему образу стен, а также образование зон разрушения стены в окрестностях оконных и дверных проемов, что позволяет уточнить инженерные решения при усилении здания. На рис. 7 показаны напряжения в шпильке усиления на одном из этапов подьема.
Выводы
Обоснованы требования к механической модели, моделирующей процесс отрыва здания от фундамента при увеличении усилий на домкраты.
Сформулированы основные физические зависимости, определяющие процесс образования линии отрыва в слое адгезии. Также возможен учет разрушения в фрагментах стен над домкратными нишами.
Приведенные зависимости позволяют учитывать конструктивную нелинейность, связанную с изменением расчетной схемы при постепенном отрыве здания от фундамента.
1. Makhviladze L.S., Sheradze G., Zotov V.D., Bolotov Yu.K. Restoration of operational reliability of emergency buildings. - "Engineering problems of Georgia: status and prospects". - Tbilisi: Engineering Academy of Georgia, 1998 - P.121-123.
2. Lobov O.I., Gapeev V.I., Zotov V.D., Bolotov Yu.K., Zotov M.V. Lifting and leveling emergency buildings. - "Industrial and civil construction". - Moscow:, 1999.- P.14-16.
3. Zotov M.V., Kutasov I.A., Skibin M.G., Firichenko A.A. Technological features of eliminating excessive tilts of semi-detached buildings of different number of storeys. - "Foundations, foundations and soil mechanics". - Moscow:, 2015. - P.11-14
4. Pshenichkina V.A., Gordeev S.S., Ivanov M.A. Monitoring of buildings, risks, safety of construction sites, monitoring of building structures. - Proceedings of the international scientific and practical conference "Low-rise construction". Volgograd: VSUACE, 2009. 484 p.
5. Panasyuk L.N., Tyurina V.S., Chubka Yu.Sh. Modeling of reinforced landslide slopes performance using the finite element method // Engineering Bulletin of the Don.-2016, No. 3.http://www.ivdon.ru/ru/magazine/archive/n3y2016/3733
6. Panasyuk L.N., Zotova E.V., Ho Chantho, Akopyan V.F. Determination of the influence of an auxiliary grillage on the bearing capacity of a pile for reinforcing a basement building, taking into account uneven settlement in Belovo, Kemerovo Region.- Engineering Bulletin of the Don, Rostov-on-Don, 2013, No. 2, p. 131 EDN: https://elibrary.ru/QLISYH
7. Panasyuk L.N., Tyurina V.S., Chubka Yu.Sh., Poshev A.U-B. Modeling of landslide slope performance under dynamic impact // Engineering Bulletin of the Don. 2018. No. 2 http://www.ivdon.ru/ru/magazine/archive/N2y2018/4901
8. Panasyuk L.N., Tyurina V.S., Savelyeva N.A., Chubka Yu.Sh. Dynamic response in the "road structure-landslide slope" system from traffic // Engineering Bulletin of the Don. 2018. No. 4 http://www.ivdon.ru/ru/magazine/archive/n4y2018/5376
9. Panasyuk L.N., Trufanova E.V. Application of the Klen-MKD software package for calculations in a nonlinear formulation: - "Actual problems of science and technology". - Rostov-on-Don, 2024.-953-954s. EDN: https://elibrary.ru/OMDYSP
10. Rzhanitsyn A.R. Calculation of structures taking into account the plastic properties of the material. Moscow: Gosstroyizdat. 1954. 129 p.
11. Pisarenko G.S., Lebedev A.A. Resistance of materials to deformation and destruction under complex stress state. Kiev: Naukova Dumka, 1969. 211 p.
12. Filonenko-Borodich M.M. Mechanical theories of strength. Moscow: Moscow State University Press, 1961. 91 p.
13. Rabotnov Yu.N. Mechanics of deformable solids. Moscow: Nauka, 1979. 650 p.
14. Panasyuk L.N., Kravchenko G.M. Stability of direct circuits integrating the equations of motion in the simulation of the dynamics of destruction // MATEC «Web of Conferences» 2017
15. Panasuk L.N., Kravchenko G.M., Trufanova E.V. Researching design solutions for frames of buildings in the case of increased seismic intensity in specific zones // Matec Web of Conferences. 2017 №106.DOI: doi.org/10.1051/matecconf/201710602027
16. Panasyuk L.N. On the construction of explicit unconditionally stable schemes of direct integration of the problem of the dynamics of structures // News of universities. Construction, 1995. № 10, pp. 35-40.



















