Russian Federation
employee
Moskva, Moscow, Russian Federation
Russian Federation
UDK 519.8 Исследование операций
UDK 531 Общая механика. Механика твердых тел
UDK 534 Механические колебания. Акустика
UDK 539.2 Свойства и структура молекулярных систем
UDK 539.6 Межмолекулярные силы
UDK 620.9 Общая энергетика
UDK 624.042 Расчет нагрузок и напряжений
UDK 624.044 Расчет деформаций
UDK 699.8 Мероприятия по защите зданий, сооружений и конструкций. Изоляционные работы. Противоаварийные мероприятия
The amplitude-frequency characteristics of vibrations of structural elements of buildings and structures are important design parameters when analyzing changes in the stress-strain state of a building during operation, including during surveys and monitoring of the technical condition of the building. Standardization of the method for determining the values of these parameters is carried out in accordance with the requirements of GOST 8.009 to ensure compliance with the requirements of GOST 31937 and GOST 32019. The vibrations of a building are a superposition of their own and forced vibrations caused by various internal (operation of household appliances and various technical systems of the building) and external (urban transport, construction sites, etc.) influences. To determine the values of the period, as a rule, the building's own vibrations are recorded, caused by the natural dynamic natural and man-made background of the city (if there is equipment sensitive to the levels of natural dynamic impact), therefore, no additional effects are exerted on the building during the measurement process. Industrial buildings are characterized by the presence and movement of heavy technological equipment inside buildings. Stresses during fluctuations have an alternating character, therefore they can cause fatigue of the material from which the structure is made. This, in turn, leads to the destruction of individual elements of the structure and, as a result, to accidents. The paper presents a dynamic calculation of the elements of the structure consisting of several stages: the dynamic characteristics of the nodes of the joints of the constructs with each other are determined; the dynamic degrees of freedom are determined; the theoretical calculation for vibrations is formalized.
dynamics, stability, natural oscillations, amplitude, angular frequency, eigenvalues, eigenvector
Введение
Динамический расчет [1] в работе проведен для проверки формализованных алгоритмов динамических расчётов допустимости внутренних усилий и перемещений с точки зрения выполнения требований прочности, жесткости и выносливости, санитарно-гигиенических норм, технологии производства ]2,3]. При невыполнении допустимых норм возникает необходимость в уменьшении уровня колебаний. Из-за различных внешних воздействий на здания и сооружения и их конструктивные элементы, а также из-за динамических реакций конструктивных элементов и зданий в целом на эти воздействия, - элементы зданий подвержены сложным импульсным динамическим колебательным процессам с различными частотами и амплитудами. Предполагаемый вариант поведения конструктивов здания представлен на рис.1:
Рис.1. Вариант колебаний конструктивных элементов зданий с представлением колебательных процессов соответствующими расчётными схемами
Целью настоящей работы является возможная формализация и автоматизация процесса поиска динамических реакций элементов зданий и сооружений на внешние импульсные воздействия разной природы.
Методы исследований
Для определения динамических взаимодействий изучаемых объектов друг с другом и с несущим остовом здания [4,5] разработана специальная схема, рис. 2:
Рис. 2. Расчётная схема для определения динамических реакций связей
при возможном вращении элементов здания вокруг вертикальной оси «Z»,
Уравновешивание приведенной на рис. 2 системы сил выполняется в точках «А» и «В». Поэтому, эти точки представляются концентраторами реактивных сил на внешние воздействия. Составив проекционные условия кинетостатического равновесия [6], получим систему уравнений равновесия сил и моментов:
$X_{Адин}+X_{Вдин}+my_C \ddot φ +mx_C \dot φ^2=0$
$Y_{ Адин}+Y_{ Вдин} + my_ C \ddot φ + my_ C \dot φ^ 2 =0$
$Z_{ Адин}=0$
$Y_{ Адин}|Z_A|+ Y_{ Вдин}|Z_B| + I_{xz} C \ddot φ - I_{yz}C \dot φ^ 2 =0$
$-X_{ Адин}|Z_A|+ X_{ Вдин}|Z_B| + I_{yz} C \ddot φ - I_{xz}C \dot φ^ 2 =0$
где XАдин, XВдин, YАдин, YВдин — соответствующие динамические реакции связей в форме реакции на импульсные динамические воздействия. Формализованная реализация алгоритма символьного решения системы уравнений равновесия представлена на рис. 3:
Рис. 3. Реализация формализации алгоритма
символьного нахождения динамических реакций связей в точках «А» и «В»
Очевидно, что характер взаимодействия связей на расчетной схеме, а по существу узлов крепления с несущими конструкциями зданий, носит явно выраженный импульсно-динамический характер {7}. Построим эпюры динамических воздействий (М) [8,9] при двух частотах возмущающей нагрузки:
Таблица 1
|
1, м |
h, м |
q, кН/м |
Р, кН |
m, кНм |
|
9 |
6 |
1 |
20 |
30 |
Составим расчётную схему, рис. 4:
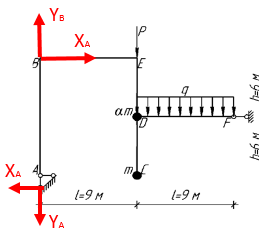
Рис. 4. Расчётная схема узла соединения элементов здания
с сосредоточенными в точках «А» и «В» массами
Результаты исследований
Число степеней свободы массы приведенной системы: n = 2. Величина сосредоточенных масс: m1 = m; m2 = m + a m = m + 2m = 3m. Составим частотное уравнение. Определим спектр частот собственных колебаний. Найдём формы собственных колебаний. Запишем уравнения частот в общем виде:
$\begin{pmatrix}
δ_{11}∙m_1-μ_1 & δ_{12}∙m_1 \\
δ_{21}∙m_2 & δ_{21}∙m_2-μ_2 \\
\end{pmatrix}=0$;
$μ=\frac{1}{ω^2}$
Приложим единичные усилия по направлению колебаний сосредоточенных масс, построим единичные эпюры моментов, и определим коэффициенты указанного «векового» уравнения, рис. 5:
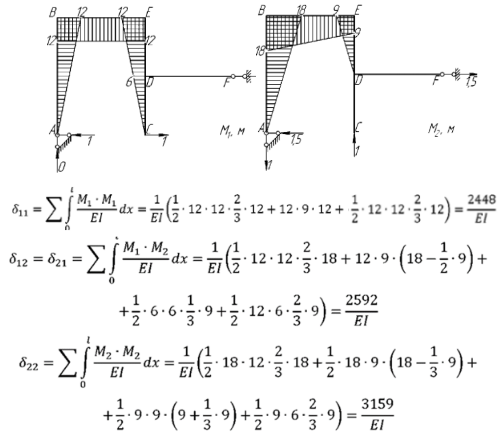
Рис. 5. Определение коэффициентов уравнения
Составим характеристическое уравнение:
$(μ_1)^2-\frac{11925∙m}{EI}∙μ_1+\frac{3044304∙m^2}{EI^2}=0; μ_1=\frac{11664∙m}{EI}; μ_2=\frac{261∙m}{EI}$
Определим частоты собственных колебаний конструктивов узла:
$ω_1=\sqrt{\frac{1}{μ_1}}=\frac{1}{108}∙\sqrt{\frac{EI}{m}} ; ω_2=\sqrt{\frac{1}{μ_1}} =frac{1}{16.155}∙\sqrt{\frac{EI}{m}}$;
Выберем минимальное значение из двух значений частот собственных колебаний:
$ω_{min}=ω_1=\sqrt{\frac{1}{μ_1}=\frac{1}{108}∙\sqrt{\frac{EI}{m}$;
Формы колебаний найдём, переписав систему уравнений следующим образом:
$\begin{pmatrix}
(δ_{11}∙m_1-μ_1)∙v_1 & (δ_{12}∙m_1)∙v_{2i} \\
δ_{21}∙m_2∙v_1 & (δ_{21}∙m_2-μ_2)∙v_{2i} \\
\end{pmatrix}=0$;
Будем считать, что
Будем считать, что (i=2)
Представим обе формы колебаний рис. 6:
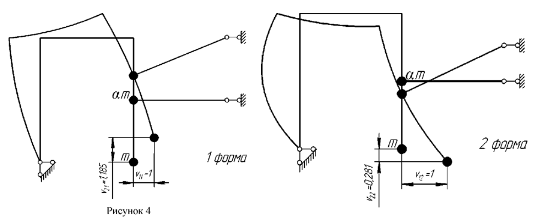
Рис. 6. Первая и вторая формы найденных колебаний
Построим эпюру моментов от амплитудных нагрузок, рис. 7:
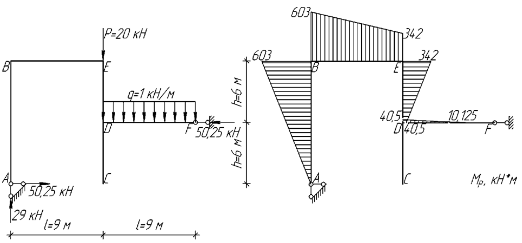
Рис. 7. Эпюры моментов от амплитудных нагрузок
Определяем свободные члены системы канонических уравнений, рис. 8:
Рис. 8. Формализованный алгоритм и значения свободных членов системы канонических уравнений
Запишем систему канонических уравнений для определения амплитудных значений инерционных сил:
$\begin{cases}
δ_{11}^*∙x_1+δ_{12}∙x_2+∆_{1p}=0 \\
δ_{22}∙x_1+δ_{22}^*∙x_2+∆_{2p}=0
\end{cases}$
Вычислим главные коэффициенты системы канонических уравнений:
Тогда
$δ_{11}^*=δ_{11}=-\frac{1}{m_1∙θ^2}=\frac{2448}{EI}-\frac{1}{m∙\frac{1}{135}∙\sqrt\frac{EI}{m}0^2}=-\frac{2916}{EI}$
$δ_{22}^*=δ_{22}=-\frac{1}{m_2∙θ^2}=\frac{3159}{EI}-\frac{1}{3m∙\frac{1}{135}∙\sqrt\frac{EI}{m}0^2}=-\frac{2916}{EI}$
Решая систему канонических уравнений определяем амплитудные значения инерционных сил x1 = -13,968 [кН] и x2 = -49,833 [кН]. Теперь можно построить «исправленную» динамическую эпюру моментов, рис.10, с учётом
Рис. 9. Построение динамической эпюры моментов
Заключение
Вывод 1. Задача расчёта на импульсную динамическую нагрузку узла соединения элементов здания формализована.
Вывод 2. Задача расчёта на импульсную динамическую нагрузку узла соединения элементов здания автоматизирована.
1. Kalinin, A.A., Petukhov, V.V. Vibrations of an elastic system with two degrees of freedom: a course of lectures / A.A. Kalinin, V.V. Petukhov - Vitebsk: UO"VSTU", 2009. - 69s.
2. Maslennikov A.M. Fundamentals of dynamics and stability of core systems: Textbook /LLC “Publishing House of the DIA", St. Petersburg State archit.- builds.un-t,-M.; St. Petersburg, 2000.-204 p.
3. Butenin N.V. et al. Course of theoretical mechanics: Studies.the manual for students of higher education institutions on technology. spec.:In 2 volumes/ N.V.Butenin, Ya.L.Lunts, D.R.Merkin. SPb.:Lan.-5th ed., ispr. 2008.-729 s
4. Numerical methods for solving problems of structural mechanics: Reference. manual / V. P. Ilyin, V. V. Karpov, A.M. Maslennikov; Under the general editorship of V. P. Ilyin. - Minsk: Vysheysh. shk., 1990. - 349 p.
5. Targ S.M. Short course of theoretical mechanics: Studies for higher education institutions/S.M.Targ.-15th ed., ster. - M.: Higher School, 2008.-415 p.
6. Feodosiev V.I. Resistance of materials: Textbook for students of higher technical studies - 10th ed., reprint. and additional - M.: Publishing House of the Bauman Moscow State Technical University, 2008. - 588 p.
7. Smirnov A.F. Stability and vibrations of structures. - M.: Transzheldorizdat, 1958. -572s
8. Kantorovich L.V., Krylov V.I. Approximate methods of analysis. M.: Gostekhizdat, 1952. 692 p.
9. Lukashevich A.A. Modern numerical methods of structural mechanics: A textbook. - Khabarovsk: Publishing house of Khabar. state. tech. un-ta, 2003. - 135 p.
