Russian Federation
Moscow, Russian Federation
Russian Federation
UDC 620.9
UDC 692
The paper considers aspects of the reactive behavior of structural elements of large-panel buildings. The problem of determining the position of the centers of mass in the process of interaction of the studied objects is solved, thus allowing us to evaluate the kinetics of the behavior of structural elements. Calculation schemes for determining dynamic reactions in the connections of structural elements under pulsed dynamic action on buildings and structures are proposed. A system of forces of the elements under consideration, balanced by inertial internal and external influences, has been compiled. An interpretation of the behavior of structural elements by an oscillator, a circuit producing a continuous, repetitive, variable wave head start, is proposed. This made it possible to quantify the change in the kinetic energy of structural elements when exposed to each other. An algorithm for determining dynamic reactions in the junctions of structural elements has been developed.
forecast, position of a point in space, dynamic coupling reaction, calculation scheme, oscillator, mathematical pendulum, main vector, kinetic moment, kinetic energy change, phase spaces, synergetics, attractor
Введение, и актуальность, научная значимость
Изучение реактивного поведения конструктивных элементов панельных зданий сосредоточено на анализе поведения узлов крепления панелей к несущему остову здания.
Реакции узлов крепления панелей зданий на внешние динамические воздействия зависят от конструкции узлов и типа воздействия.
При воздействии ветра или землетрясения возможны поворот или деформация крепежных элементов. Следствия динамики импульсных воздействий могут проявляется в увеличении напряжений в отдельных, или во всех крепежных элементах, что является причиной их разрушения или отклонения от предназначенного положения.
Динамические нагрузки на узлы приводят к увеличению динамических нагрузок на несущий остов здания, что увеличивает риск его разрушения, рис. 1.
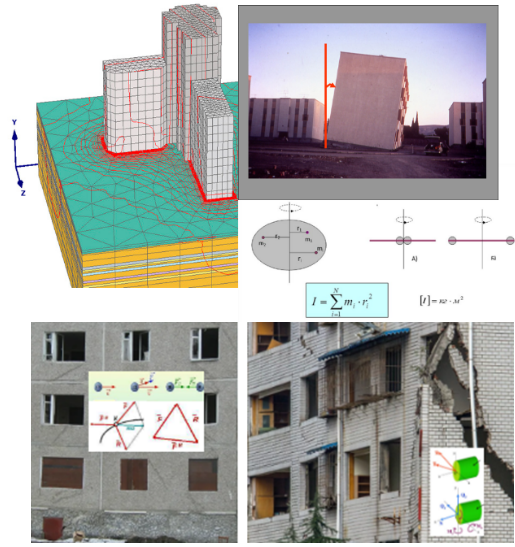
Рис. 1. Фрагменты аварийного состояния объектов
На рис. 1 показаны фазовые пространства и фазовые траектории изучаемых объектов. Совокупность всевозможных мгновенных состояний физической системы; а также пространство, элементы которого (фазовые точки) представляют (изображают) всевозможные мгновенные состояния системы (принцип Д’Аламбера).
Приведены векторные схемы механизмов формирования внутренних напряжений инерциальными движениями тел, представленными материальными точками, аттракторами, как причины разрушений и аварий. Аттрактор – компактное подмножество фазового пространства динамической системы, все траектории из некоторой окрестности которого стремятся к нему при времени стремящемуся к бесконечности. Аттрактором может являться притягивающая неподвижная точка, периодическая траектория, или некоторая ограниченная область с неустойчивыми траекториями внутри.
Циклические динамические воздействия в виде множеств движений совокупностей аттракторов, можно охарактеризовать синергетическим процессом их самоорганизации для поддержания временной устойчивости рассматриваемых объектов и возможным в последствии распадом (разрушением) структур самой различной природы. Синергетика — междисциплинарная область науки, изучающая, как сочетаются и объединяются объекты друг с другом.
Таким образом, для обеспечения безопасности необходимо:
- читывать возможные внешние и внутренние циклические воздействия, в т. ч. и при монтажных работах,
- спользовать качественные материалы, а также надежный крепеж.
Методики исследований и модели, принятые в работе
Вибрационно-динамическое воздействие может приводить к различным типам поведения элементов крепления панелей зданий в узлах крепления, включая сферическую траекторию поведения [1]. При воздействии динамических нагрузок элементы крепления панелей могут колебаться в разных направлениях. Это приводит к появлению сферической траектории поведения [2].
Взаимодействия изучаемых элементов представлено в виде поведения различных синергетических систем [3], рис. 2:
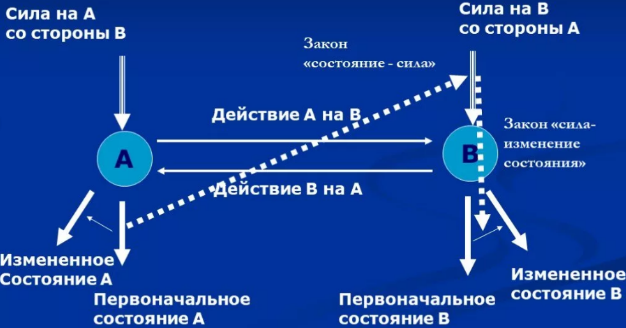
Рис. 2. Обобщённая схема динамики взаимодействия конструктивных элементов,
узлов крепления панелей и их материальных точек
Действия и противодействия рассматриваемых элементов предполагает, что при каждом взаимодействии узлов и конструктивных элементов (тел), сила, с которой первое тело действует на второе, равна по модулю, но противоположна по направлению силе, с которой второе тело действует на первое [4].
Таким образом, любое воздействие вызывает противодействие равной силой в противоположном направлении.
Это вызывает динамические реакции в узлах крепления, которые динамически воздействуют на несущий остов здания. Узлы крепления панелей являются частью системы, которая связана с несущим остовом здания. Поэтому любые изменения в узлах крепления вызывают изменения и в несущем остове. При динамическом воздействии на здания происходят циклические колебания, которые передаются через узлы крепления на несущий остов и влияют на его динамические характеристики [5].
Основные положения используемого метода исследования
На основе кинематических данных (координат, скоростей и ускорений) определены кинетическая и потенциальная энергии системы. С помощью уравнений кинематики найдены производные от функций координат и скоростей, и подставлены в уравнения динамики аттракторов.
Внешнюю систему сил к исследуемым системам, — привели к «уравновешенной системе сил» методом последовательного уравновешивания. В дискретный момент времени, кроме внешних воздействий к изучаемой системе — приложена соответствующая сила инерции $\overrightarrow{Ф}$ к центру приведения, [6]. Определим вектор силы, - равный главному вектору сил инерции, и вектор момента, равный - главному моменту сил инерции относительно центра приложения, т.е. (центра масс рассматриваемых конструктивных элементов):
$\overrightarrow{Ф}=-m\overrightarrow{a_c}$; (1)
$\overrightarrow{M_с^Ф}=\frac{d\overrightarrow{K_c}}{dt}$ (2)
где $\overrightarrow{K_c}$ — кинетический момент рассматриваемых элементов относительно центра масс (точки С). Момент импульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина зависящая от того, сколько массы вращается, как она распределена относительно оси.
В случае вращения элемента, имеющего плоскость материальной симметрии вокруг оси проходящей через центр масс перпендикулярно этой плоскости, систему сил приведём к паре сил, лежащей в плоскости материальной симметрии элемента. Для тела любая плоскость, проходящая через ось вращения, является плоскостью материальной симметрии. В математике рассматриваются различные виды симметрий, в т.ч.: осевая симметрия (с), -(с) относительно прямой, центральная (с).-(с) относительно точки, зеркальная (с).-(с) относительно плоскости.
Вектор момента этой пары определим следующим равенством:
$\overrightarrow{M_{Cz}^Ф}=\frac{d(I_{Cz}\overrightarrow{\omega})}{t}=-I_{Cz}\overrightarrow{\epsilon}$ (3)
где I_Cz - момент инерции относительно оси, проходящей через центр масс.
Алгебраический момент пары сил инерции определим в виде:
$M_{Cz}^Ф=-I_{Cz}\epsilon_z=-I_{Cz}\omega_z=-I_{Cz}φ ̈ $ (4)
При плоском движении рассматриваемых объектов здания, имеющих плоскость материальной симметрии, систему сил инерции приведём к силе и к паре сил, лежащих в плоскости материальной симметрии:
$\overrightarrow{Ф}=-m\overrightarrow{a_c} $, (5)
$M_{Cz}^Ф=-I_{Cz}\epsilon_Z$ (6)
где $I_{Cz}$ — момент инерции относительно оси, проходящей через центр масс перпендикулярно плоскости материальной симметрии.
Для определения динамических реакций от взаимодействий объектов друг с другом, и с несущим остовом здания, рассмотрим их импульсно- циклические повороты вокруг вертикальных и горизонтальных швов между соответствующими конструкциями зданий на незначительный угол, рис. 3.
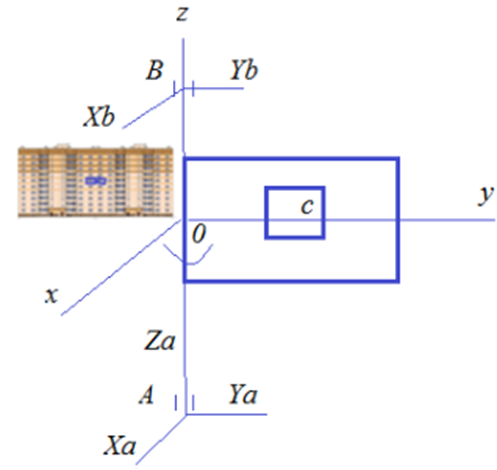
Рис. 3. Схема для определения динамических реакций в узлах крепления
(при возможном знакопеременном вращательном движении элемента вокруг оси 0Z на незначительный угол в габаритах шва)
Составив проекционные условия равновесия — получим статически определимую систему уравнений равновесия сил и моментов (7):
$\begin{pmatrix}
X_{Адин}+X_{Вдин}+my_{C} φ ̈+mx_C φ ̇^2=0 \\
Y_{Адин}+Y_{Вдин}+mx_{C} φ ̈+my_C φ ̇^2=0 \\
Z_{Адин}=0 \\
Y_{Адин}|z_A |-Y_{Вдин} |z_B |+I_{xz} φ ̈-I_{yz} φ ̇^2=0\\
-X_{Адин} |z_A |+X_{Вдин} |z_B |+I_{yz} φ ̈-I_{xz} φ ̇^2=0 \end{pmatrix}$ (7)
где $X_{Адин},X_{Вдин},Y_{Адин},Y_{Вдин}$ искомые динамические реакции связей в точках «А» и «В», указанные на рис.3.
Из системы уравнений (7) стандартным образом выражаются все неизвестные значения $X_{Адин},X_{Вдин},Y_{Адин},Y_{Вдин}$.
Цели и задачи
- Найти уравнение движения заданной материальной точки, принадлежащей исследуемому объекту. Материальная частица, обладающая массой, — тело, размерами, формой, вращением и внутренней структурой которого можно пренебречь в условиях исследуемой задачи. Положение в пространстве определяется как положение геометрической точки и может в т. ч. задаваться радиус-вектором.;
- Найти реакции опор в узлах крепления конструкций от импульсно-динамических воздействий;
- Разработать алгоритм решения задач, указанных в п.1 и п.2.
Общие положения для разработки алгоритма
Для определения динамических реакций используем расчётную схему, рис. 4.
Будем считать, что кинетика динамического поведения аналогична поведению осциллятора — cистемы, совершающей колебания, показатели которой периодически повторяются во времени. Осциллятор представим в виде математического маятника — механической системы, состоящей из материальной точки на конце невесомой нерастяжимой нити или лёгкого стержня и находящейся в однородном поле сил тяготения. Другой конец нити (стержня) обычно неподвижен. Представим математический маятник относительно точки «0» с углом отклонения от положения равновесия, равным «φ».
Прямоугольную панель здания размерами (l ×h) и массой «m», обозначим грузом «Р», который с помощью условно-невесомого стержня длиной «L» прикрепим к узлу-шарниру, в точке 0 , как это показано на рис. 4:
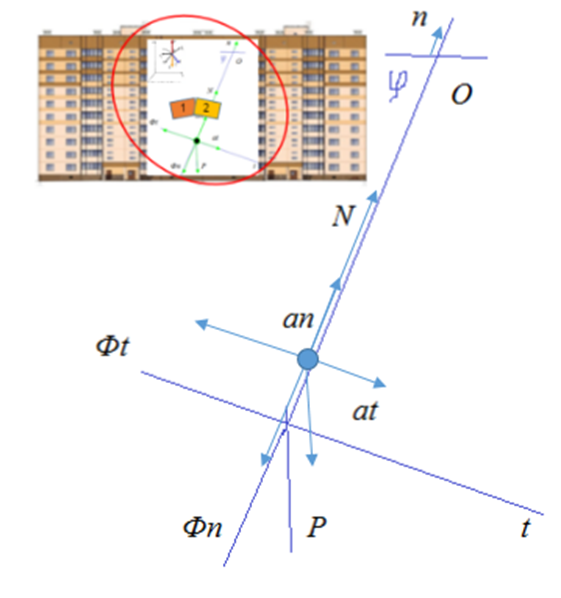
Рис. 4. Схема для определения динамической реакции связи указанного осциллятора
при периодическом отклонении от положения равновесия и уравновешивание системы сил
Обсуждение результатов, (алгоритм)
Инструкция 1. Схематично представим фрагмент модели осциллятора с начальным углом поворота, равным «φ», рис. 4. Угол поворота будем отсчитывать от начального равновесного положения.
Инструкция 2. Определим силы, представленные на схеме, как силу тяжести, равную «$\overrightarrow{P}=m\overrightarrow{g}$», и силу внутреннего усилия в стержне «$\overrightarrow{N}$», как реакцию опоры обозначенного стержня.
Инструкция 3. Рассмотрим естественные силы, Сила, действующая по направлению нормали к рассматриваемой траектории движения равна «$\overrightarrow{Ф_n}=-m\overrightarrow{a_n} $». Сила, действующая по направлению касательной линии к рассматриваемой траектории движения, равна «$\overleftarrow{Ф_τ}=-m\overleftarrow{a_τ} $» силы инерции. При этом $a_n=\frac{v^2}{l}$ и $a_π=\frac{dv_τ}{dt}$, имея ввиду, что $v=∫a∙dt$»,
С учётом введенных обозначений, обозначенного, — уравновесим расчётную схему обозначенными естественными силами.
Представим искомую реакцию опоры в виде ($\overrightarrow{N_R}$), действующую по направлению линии, соединяющей «груз» с опорой, одним из элементов множества уравновешенной системы сил: $\begin{cases}\overrightarrow{P},\overrightarrow{N_R},\overrightarrow{Ф_n },\overrightarrow{Ф_τ }\end{cases}\$.
Рассмотрим уравнения равновесия:
$\sum^n_k=_1F_{kτ}=0, m∙g∙cos(φ)-Ф_τ=0$ (8)
$\sum^n_k=_1F_{kn}=0, N_R-Ф_n-m∙g∙sin(φ)=0$ (9)
Отсюда:
$m\frac{dv_τ}{dt}=m∙g∙cos(φ); и N_R=m∙g∙sin(φ)+\frac{mv^2}{l}$ (10)
Произведём замену переменной в дифференциальном уравнении и определим скорость движения точки массой равной «m».
«Груз» висит на «связи», представляющей собой крепление конструктивного элемента к несущему остову здания, в которой возникает «нормальное» усилие $N_R$.
$\frac{dv_τ}{dt}=\frac{dv_τ}{dφ}∙\frac{dφ}{dt}=ω∙\frac{dv_τ}{dφ}$ ,при том, что $ω=\frac{v_τ}{l}$ (11)
В результате замены переменной дифференциальное уравнение движение узла панели принимает следующий вид
$\frac{v_τ}{l}∙\frac{dv_τ}{dφ}= m∙g∙cos(φ)$, при начальном условии $v_τ |_{φ=0}=0$ (12)
Решая дифференциальное уравнение:
$∫_0^{v_τ}v_τ∙dv_τ=g∙l∙∫_0^φcos(φ)∙dφ$ (13)
получаем выражение уравнения кинематики:
$\frac{v_τ^2}{2}=g∙l∙sin(φ)$ (14)
Используя найденную ранее скорость движения, найдём модуль значения $N_R$:
$N_R=3∙m∙g∙sin(φ)$ (15)
Из (15) следует, что рассмотренные элементы совершают движения, в основе которых лежат собственные и вынужденные колебания с периодом:
$T=2∙π∙\sqrt{\frac{L}{g}}$ (16)
где «L» габариты связи.
Крое этого, период колебаний пропорционально зависит от массы, жесткости и демпфирования элементов конструкции, а также от величины внешних динамических нагрузок [7].
Заключение
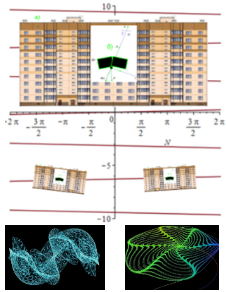
Рис. 5. Осцилятрная интерпретация поведения связей
при синергетическом взаимодействии узлов креплений с несущим остовом здания
На рис. 5 представлены циклические (12) колебания конструктивных элементов, на угол отклонения «φ» от положения равновесия, на рисунке — от горизонтали.
Для моделирования поведения узла крепления панели к зданию как синергетического аттрактора, используем уравнения Лоренца [8]. Уравнение описывает динамику системы, которая проявляет хаотическое поведение:
$\begin{cases}\frac{dx}{dt}=σ(y-x) \\ \frac{dy}{dt}=x(ρ-z)y \\ \frac{dz}{dt}=(xy-βz) \end{cases}$ (17)
где — x, y и z переменные состояния системы; σ, ρ и β — параметры, которые можно настроить для получения желаемого поведения.
Для моделирования поведения узла выбираются определенные начальные значения x, y и z, соответствующие начальным условиям системы [9]. Затем используется система уравнений Лоренца для расчета изменения этих переменных во времени.
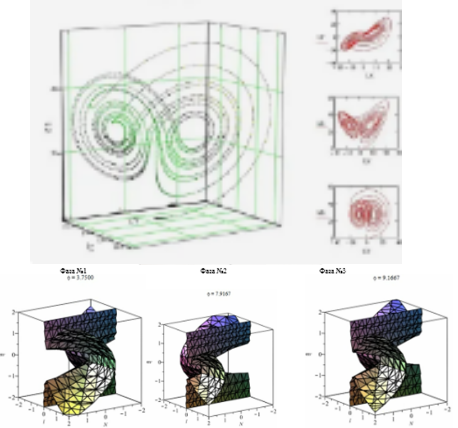
Рис. 6. Модель синергетического аттрактора узлового крепления панели к несущему остову панельного здания
На рис 6 показаны стадии [8, 9] изменения динамики поведения точечного виртуального осциллятора-аттрактора при углах поворота равных «φ =3,75 град и φ = 9,17 град» соответственно.
Выводы
- Решена задача определения положения материальной точки конструктивного элемента в дискретный момент времени в пространстве;
- Представлен метод определения динамических реакций связей при импульсном динамическом взаимодействии;
- Показана динамика реактивного поведения элементов зданий точечными и обобщенными осцилляторами.
- Установлено гармоническое изменение состояний исследуемых объектов от импульсных динамических воздействий и, что период изучаемых колебаний прямо пропорционален корню квадратному из отношения «$\frac{L}{g}$».
- Предположено, что последствия различных внешних деструкций могут являться следствием инерциального и реактивного вибрационного поведения конструктивных элементов.
1. Zhang, X., Li, H., Li, Y., & Li, Q. (2018). Seismic response of a tower structure with energy dissipation dampers using an inverse compensation control strategy. Engineering Structures, 176, Pp. 778-792.
2. Kantorovich L.V., Krylov V.I. Approximate methods of analysis. M.: Gostekhizdat, 1952. 692 p.
3. Numerical methods for solving problems of structural mechanics: Ref. allowance / V. P. Ilyin, V. V. Karpov, A. M. Maslennikov; Under total ed. V. P. Ilyin. - Minsk: Vysh. school, 1990. - 349 p. EDN: https://elibrary.ru/UGDTKB
4. Huang, Q., Li, J., & Zhang, L. (2019). A comparative study of the linear and nonlinear dynamic analyses for tall buildings under strong earthquake excitation. Soil Dynamics and Earthquake Engineering, 118, 293-307
5. Smirnov A.F. Stability and vibrations of structures. - M .: Transzheldorizdat, 1958. -572 p.
6. Luo, M., Yang, Y., & Chen, Z. (2021). Experimental study on the dynamic performance of a passive hybrid control system for seismic protection of bridges. Engineering Structures, 234, 111817.
7. Huang, Q., Li, J., & Zhang, L. (2019). A comparative study of the linear and nonlinear dynamic analyses for tall buildings under strong earthquake excitation. Soil Dynamics and Earthquake Engineering, 118, 293-307.
8. Li, C., Li, J., & Li, B. (2022). A novel fiber-optic sensing technique for structural damage detection and health monitoring. Measurement, 187, 109516


















