from 01.01.2003 until now
Russian Federation
VAC 2.1.2 Основания и фундаменты, подземные сооружения (Технические науки)
VAC 2.1.3 Теплоснабжение, вентиляция, кондиционирование воздуха, газоснабжение и освещение (Технические науки)
VAC 2.1.5 Строительные материалы и изделия (Технические науки)
VAC 2.1.6 Гидротехническое строительство, гидравлика и инженерная гидрология (Технические науки)
VAC 2.1.7 Технология и организация строительства (Технические науки)
VAC 2.1.8 Проектирование и строительство дорог, метрополитенов, аэродромов, мостов и транспортных тоннелей (Технические науки)
VAC 2.1.9 Строительная механика (Технические науки)
VAC 2.1.10 Экологическая безопасность строительства и городского хозяйства (Технические науки)
VAC 2.1.11 Теория и история архитектуры, реставрация и реконструкция историко-архитектурного наследия (Технические науки)
VAC 2.1.12 Архитектура зданий и сооружений. Творческие концепции архитектурной деятельности (Технические науки)
VAC 2.1.13 Градостроительство, планировка сельских населенных пунктов (Технические науки)
VAC 2.1.14 Управление жизненным циклом объектов строительства (Технические науки)
VAC 2.1.15 Безопасность объектов строительства (Технические науки)
UDK 624.154.5 Буровые сваи. Набивные бетонные сваи
GRNTI 67.01 Общие вопросы строительства
BBK 308 Монтаж, эксплуатация, ремонт машин и промышленного оборудования
Engineering calculations in the spatial formulation, as well as the results of field observations, show a significant decrease in lateral displacements of the foundation pit retaining walls in the area of the corner zones. At the same time, in design practice, a large number of decisions are made on the basis of calculations in a flat formulation. For pits with a depth of more than 10 m, the influence of corner zones can make a significant contribution to the reduction of movements and, as a result, internal forces in the retaining walls and restraint systems. The underestimation of the corner effect leads to an increase of the retaining structures construction cost. This article presents the results of FEM calculations studies of the monolithic reinforced concrete wall functioning in the corner zones of pit in sandy soils. As a result, it was revealed that the movement of the diaphragm wall in the area of the corner zones of the foundation pit is influenced by such factors as: the pit depth, the angle between retaining walls, and the stiffness of the retaining wall and struts. At the same time, the properties of the sand and the stiffness of the retaining wall and struts do not affect the distribution of displacements in the corner zones.
diaphragm wall, corner effect, lateral displacements, enclosures stiffness, sandy soils, mathematical model, finite element method, foundation pit
1. Введение
Уплотнение застройки, развитие транспортной инфраструктуры в крупных городах приводит к необходимости освоения подземного пространства. Строительство подземных и заглубленных сооружений зачастую ведется в котлованах под защитой гибких подпорных стен, в том числе и стены в грунте траншейного типа.
В соответствии с требованиями действующей нормативной документацией при проектировании необходимо учитывать пространственную работу конструкций. Эти положения относятся и к расчетам конструкциям ограждения котлованов, и к расчетам оценки влияния строительства на окружающую застройку. При этом имеющиеся на сегодняшний день программные комплексы, позволяющие решать такие задачи, являются дорогостоящими, требуют определенного уровня дополнительной подготовки инженеров, а их применение не всегда обосновано при решении рядовых задач.
Многочисленные исследования ряда авторов из разных стран [2, 3, 4, 5, 8, 13, 16, 18, 20, 22] показывают, что перемещения конструкций ограждения котлованов в угловых зонах значительно меньше, чем в центральных частях. Результаты обзора, приведенные в [1], показали, что вопросы, связанные с работой конструкций ограждения в угловых зонах котлованов в песчаных грунтах, исследованы недостаточно, в том числе из-за крайне малой базы объектов исследований, располагавшихся в песчаных грунтах.
В работах C.Y. Ou [17], J.F. Roboski и R.J. Finno [7, 23], R. Fuentes и M. Devriendt [10] представлены графические и аналитические методы оценки перемещений конструкции ограждения котлована в угловой зоне в зависимости от перемещений, рассчитанных в плоской постановке задачи, выражаемые коэффициентом плоской деформации (PSR=δ/δmax), равному отношению перемещений в заданной точке ограждения к максимальным перемещениям ограждения котлована, полученным при выполнении расчетов в плоской постановке задачи. Анализ этих методик показал, что они не являются универсальными и не могут распространяться на все дисперсные грунты.
Экспериментальные исследования, проведенные авторами в составе авторского коллектива на опытном участке [1], подтвердили наличие углового эффекта. Выявлено, что в песчаных грунтах данный эффект в плане распространяется на величину, близкую к глубине котлована. При увеличении глубины котлована размер зоны влияния углового эффекта на горизонтальные перемещения ограждения котлована увеличивается.
Вместе с тем, в работе [1] показано, что для выполнения численных исследований влияния различных параметров на перемещения конструкции ограждения в угловых зонах котлована рекомендуется использовать модель упрочняющегося грунта, реализованную в программном комплексе PLAXIS 3D.
Для изучения влияния на работу конструкции ограждения котлована таких факторов, как механические характеристики грунта, жесткость конструкции ограждения и удерживающей системы, угол между смежными сторонами котлована проведены численные исследования методом конечных элементов, результаты которых изложены ниже.
2. Расчетно-теоретические исследования
На расчетно-теоретические исследования поставлены задачи оценки влияния на работу конструкции ограждения котлована в угловой зоне следующих параметров: прочность грунта, деформационные характеристики грунта, жесткость конструкции ограждения котлована, количество ярусов распорной системы, жесткость распорной системы и угол между смежными стенами ограждения.
Решение поставленных задач выполнялось численно методом конечных элементов в среде программного геотехнического комплекса PLAXIS 3D с граничными условиями пространства в горизонтальных направлениях, соответствующих на боковых границах свободным перемещениям в вертикальной плоскости и нулевым в горизонтальной, а на нижней горизонтальной границе – нулевым вертикальным и горизонтальным перемещениям. Основание принято однородным изотропным с переменной в плане мощностью и ограничением сжимаемой толщи. При расчетах использовалась модель упрочняющегося грунта (Hardening Soil).
Расчеты проводились для различных песчаных грунтов с характеристиками, представленными в таблице 1.
Таблица 1
Принятые в расчете наборы параметров модели грунта
|
№ ИГЭ |
Наименование |
е, д.е. |
ɣ, кН/м3 |
ɣd, кН/м3 |
w, % |
φ, ᵒ |
c, кПа |
Ψ |
νur |
pref, МПа |
Е50ref, МПа |
Еurref, МПа |
Еoedref, МПа |
m |
|
1 |
Песок средней крупности |
0,5 |
21,1 |
17,7 |
18,8 |
36,3 |
41,4 |
13,4 |
0,2 |
0,1 |
49,6 |
114,4 |
31,5 |
0,61 |
|
2 |
Песок мелкий |
0,5 |
21,1 |
17,7 |
18,8 |
40,6 |
21,6 |
16,1 |
0,2 |
0,1 |
31,3 |
108,9 |
25,6 |
0,78 |
|
3 |
Песок пылеватый |
0,5 |
21,1 |
17,8 |
18,7 |
41.4 |
27.6 |
17,6 |
0,2 |
0,1 |
43,8 |
106,0 |
47,4 |
0,65 |
|
4 |
Песок средней крупности |
0,53 |
18,7 |
17,3 |
10 |
36,8 |
6,1 |
10 |
0,16 |
0,03 |
10,43 |
65,1 |
7,0 |
0,92 |
В качестве конструкции ограждения котлована принята монолитная железобетонная стена в грунте траншейного типа толщиной 0,4 м, 0,6 м и 0,8 м. Для обеспечения устойчивости ограждения котлована предусматривалась распорная система из стальных труб Ø 530х10 мм, Ø 630х10 мм, Ø 720х10 мм, расположенных с шагом 5 м в плане. Количество ярусов распорок по глубине котлована определялось в зависимости от его глубины.
Анализ влияния геометрических размеров котлована
Для анализа влияния линейных размеров прямоугольного котлована было выполнено 40 расчетов в трехмерной постановке задачи, в рамках которых рассмотрены следующие геометрические размеры котлованов: длина L и ширина B котлована принимались равными 10 м, 20 м, 60 м и 100 м при отношениях B/L равными 0.1, 0.2, 0.33, 0.5, 0.6, 1.0, 2.0, 3.0, 5.0, 6.0, 10.0. Глубина котлована составляла 10 м, 15 м и 20 м при глубине заделки конструкции ограждения ниже уровня дна 5 м, 7 м и 10 м соответственно. Для котлованов глубиной 10 м, 15 м и 20 м принято 2, 3 и 4 яруса распорок соответственно. Характеристики грунта приняты для ИГЭ-1 (см. табл. 1). Ограждение котлована принято толщиной 0,6 м, распорки из стальной трубы Ø 630х10 мм.
В результате выполненных расчетов получены горизонтальные перемещения конструкций ограждения котлована, которые были рассмотрены в относительных величинах, значимость которых была установлена в процессе обзора литературных источников [6, 7, 9, 10, 11, 12, 15, 17, 21, 23, 24]. На рис. 1 представлены максимальные горизонтальные перемещения стены ограждения δ(x) длиной L в сечении на расстоянии от угла котлована x, отнесенные к максимальным перемещениям ограждения котлована δmax длиной L=100 м. По оси абсцисс рассматривается отношение расстояние от угла котлована к его глубине x/H.
За границу проявления углового эффекта принято расстояние от угла котлована, на котором выполняется условие δ(x)/δmax =0,9 (красная пунктирная линия на рис. 1). Данное условие также было предложено Ou и др. в работе [17], а само отношение δ(x)/δmax обозначается как PSR (plane strain ratio).
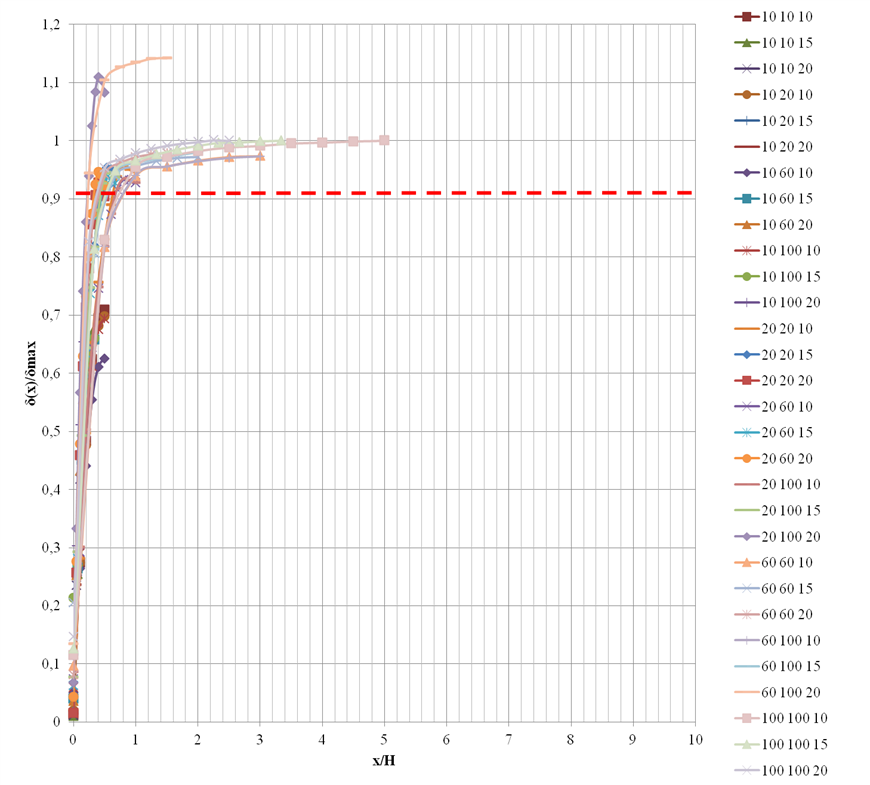
Рис. 1. Зависимость относительных перемещений ограждения котлована вдоль стороны L от относительного расстояния от угла.
В условных обозначениях записана кодировка геометрических размеров котлована в формате L B H [м]
Анализ графиков (рис. 1) позволил выбрать вид функции зависимости PSR от относительного расстояния от угла котлована x/H. Данную функцию можно представить в следующем виде:
где PSRa – значение координаты асимптоты по оси ординат δ(x)/δmax, к которой стремиться предложенная функция;
b –относительное перемещение угла котлована δ(0)/δmax;
α –коэффициент, зависящий от глубины котлована.
Для случаев, представленных на рис. 1, когда расстояние действия углового эффекта dmax не превышает L/2, были подобраны параметры функции (1) и сведены в табл. 2.
Таблица 2
Параметры функции (1) для случаев, когда расстояние действия углового эффекта dmax не превышает L/2
|
L |
B |
H |
α |
PSRa |
b |
|
60 |
60 |
10 |
3.1 |
1 |
0.1 |
|
100 |
20 |
10 |
3.1 |
1 |
0 |
|
100 |
100 |
10 |
3.2 |
1 |
0.1 |
|
60 |
60 |
10 |
3.2 |
1 |
0.1 |
|
60 |
100 |
10 |
3.2 |
1 |
0.1 |
|
20 |
10 |
10 |
3.3 |
1.05 |
0 |
|
100 |
100 |
10 |
3.3 |
1 |
0.1 |
|
100 |
60 |
10 |
3.3 |
1 |
0.1 |
|
20 |
20 |
10 |
3.5 |
1 |
0 |
|
60 |
20 |
10 |
3.5 |
1 |
0 |
|
20 |
100 |
10 |
3.5 |
1 |
0 |
|
20 |
60 |
10 |
3.5 |
1 |
0 |
|
20 |
20 |
10 |
3.5 |
1 |
0 |
|
100 |
10 |
10 |
4.3 |
1 |
0 |
|
60 |
60 |
15 |
4 |
1 |
0.2 |
|
60 |
60 |
15 |
4.3 |
1 |
0.2 |
|
100 |
100 |
15 |
4.5 |
1 |
0.1 |
|
100 |
100 |
15 |
4.5 |
1 |
0.1 |
|
60 |
100 |
15 |
4.5 |
1 |
0.1 |
|
100 |
60 |
15 |
4.7 |
1 |
0.1 |
|
100 |
20 |
15 |
5 |
1 |
0 |
|
20 |
20 |
15 |
5 |
1 |
0 |
|
20 |
100 |
15 |
5 |
1 |
0 |
|
20 |
60 |
15 |
5 |
1 |
0 |
|
60 |
20 |
15 |
5.2 |
1 |
0 |
|
20 |
20 |
15 |
5.3 |
1 |
0 |
|
20 |
10 |
15 |
5.5 |
1 |
0 |
|
100 |
10 |
15 |
5.5 |
1 |
0 |
|
60 |
10 |
15 |
5.5 |
1 |
0 |
|
20 |
100 |
20 |
6 |
1.2 |
0 |
|
60 |
100 |
20 |
6 |
1.15 |
0.15 |
|
20 |
20 |
20 |
6 |
1 |
0 |
|
60 |
60 |
20 |
6 |
1 |
0.1 |
|
100 |
20 |
20 |
6.2 |
1 |
0.1 |
|
100 |
60 |
20 |
6.2 |
1 |
0.1 |
|
20 |
20 |
20 |
6.5 |
1 |
0 |
|
60 |
20 |
20 |
6.5 |
1 |
0 |
|
100 |
100 |
20 |
6.5 |
1 |
0.15 |
|
20 |
10 |
20 |
6.7 |
1 |
0 |
|
100 |
10 |
20 |
7 |
1 |
0 |
|
60 |
10 |
20 |
7 |
1 |
0 |
|
20 |
60 |
20 |
7 |
1 |
0 |
Из таблицы 2 видно, что параметр α зависит только от глубины котлована, а незначительные флуктуации можно списать на погрешность численного решения. Значение PSRa ни от чего не зависит, и всегда будет составлять ≈1,0, кроме случаев, когда зона действия углового эффекта dmax превышает L/2.
Регрессионный анализ (рис. 2) данных таблицы 2 позволил выявить линейную зависимость между коэффициентом α и глубиной котлована H (2).
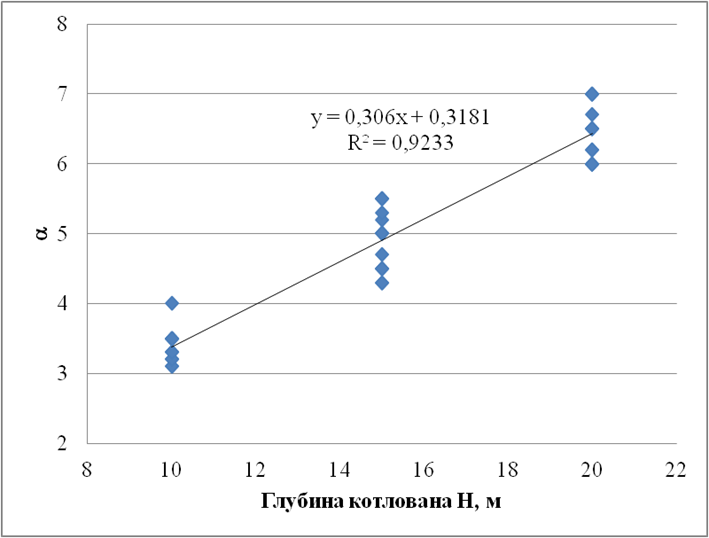
Рис. 2. График зависимости коэффициента a от глубины котлована H
Проведя математические преобразования формулы (1) и приравняв x=dmax,получим уравнение для определения границы углового эффекта при PSR=0,9, а PSRa=1
Влияние величины угла между сторонами котлована
Для исследования влияния угла между сторонами котлована на угловой эффект в ПК PLAXIS 3D была выполнена серия расчетов на модели котлована глубиной 10 м с размерами в плане 60х100 м. Ограждающая конструкция котлована – стена в грунте глубиной 15 м и толщиной 600 мм. Распорная система котлована – два яруса распорок из стальных труб Ø630х10 мм, установленных с шагом в плане 5 м. Угол между сторонами котлована θ принимался равным 45, 60, 75, 90, 105, 120 и 135 градусам соответственно.
Исследуемый угловой эффект вдоль стороны котлована оценивался по двум факторам:
– Фактор № 1: отношение максимального горизонтального перемещения стороны котлована в угловой зоне к максимальному горизонтальному перемещению стороны котлована в условиях плоской задачи (b=δ(x=0)/δmax).
– Фактор № 2: относительная величина зоны распространения углового эффекта (dmax/L).
Относительная величина зоны распространения углового эффекта определялась как отношение длины зоны, в пределах которой действует угловой эффект, к полной длине рассматриваемой стороны котлована. Для определения зоны действия углового эффекта применялся следующий критерий: максимальное горизонтальное перемещение в пределах данной зоны составляет менее 0,9 максимального горизонтального перемещения (плоская задача).
Результаты расчетов перемещений ограждающей конструкции котлована при различных углах между его сторонами представлены на рисунках 3 – 6. На данных рисунках отображена зависимость между нормализованными перемещениями (δ(x)/δmax) от нормализованного расстояния от угла котлована (x/L) и указаны границы распространения зоны углового эффекта. Из графиков (рис. 3 – 5) видно, что уменьшение угла между сторонами котлована приводит к увеличению зоны распространения углового эффекта (увеличение фактора №2). Наглядно данная зависимость продемонстрирована на рисунке 6. При этом зависимость изменения горизонтальных перемещений угла котлована от величины угла между сторонами (Фактор № 1) носит более сложный, близкий к билинейному, характер (рис. 7). Так при изменении угла θ в диапазоне от 45 до 90 градусов отношение δ(x=0) / δmax претерпевает незначительные изменения, в то время как при увеличении угла θ в диапазоне 90-135 градусов функция постоянно возрастает.
Таким образом, можно заключить следующее:
1. Величина угла между сторонами котлована существенным образом влияет на угловой эффект;
2. Уменьшение угла между сторонами котлована приводит к увеличению зоны распространения углового эффекта.
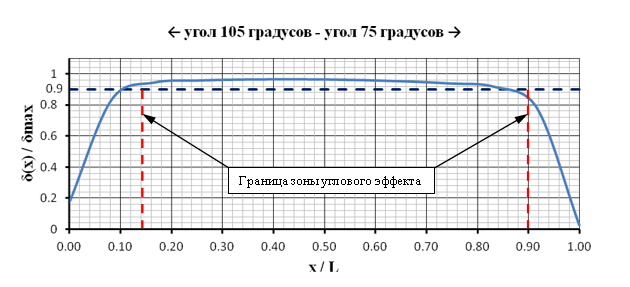
Рис. 3. Нормализованные перемещения ограждения котлована в зависимости от нормализованного расстояния от угла котлована. Острый угол между сторонами котлована равен 75°
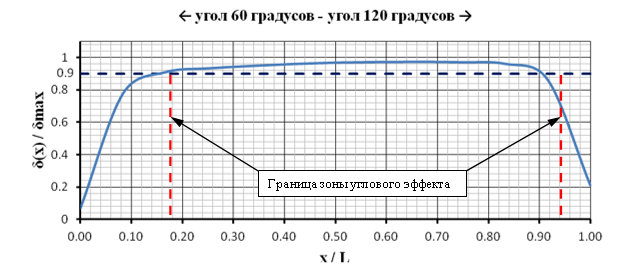
Рис. 4. Нормализованные перемещения ограждения котлована в зависимости от нормализованного расстояния от угла котлована. Острый угол между сторонами котлована равен 60°
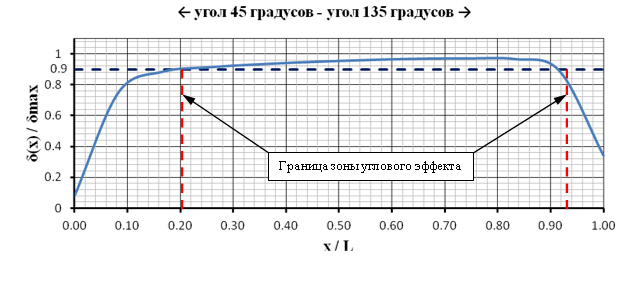
Рис. 5. Нормализованные перемещения ограждения котлована в зависимости от нормализованного расстояния от угла котлована. Острый угол между сторонами котлована равен 45°
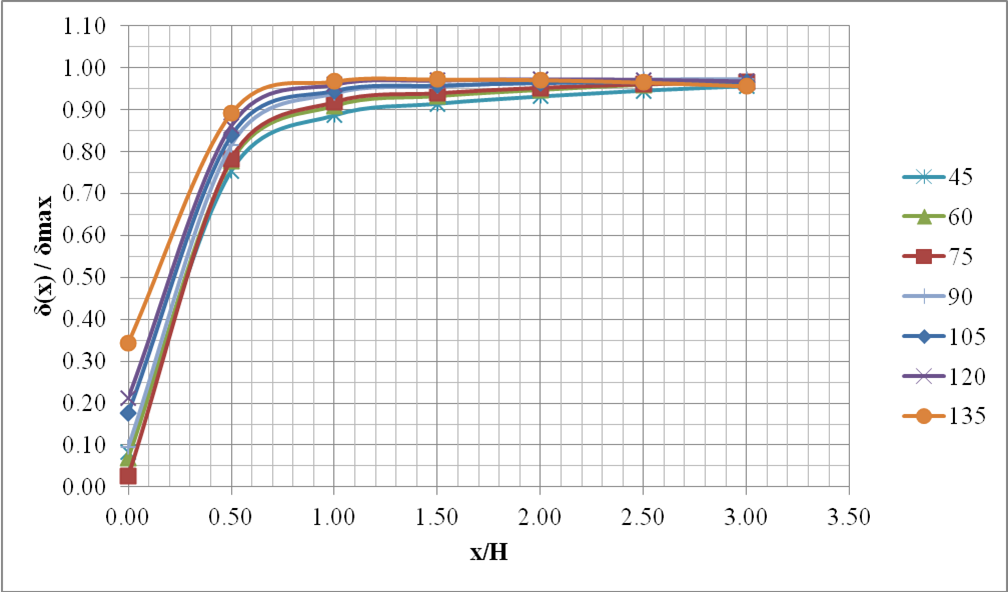
Рис. 6. Результаты расчетов стены с учетом различных значений внутренних углов между смежными стенками. В легенде цифрами указан внутренний угол между смежными стенками θ, º
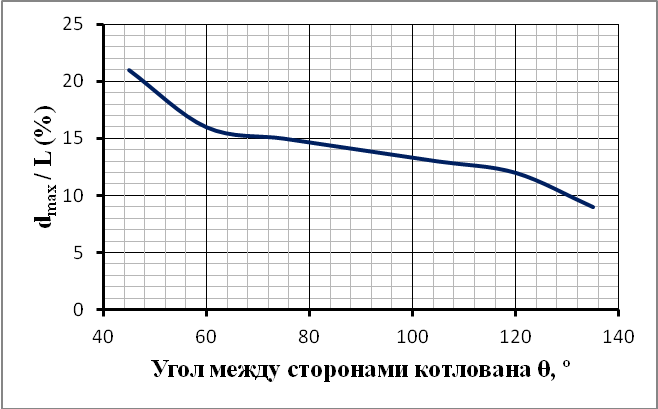
Рис. 7. Фактор №2 в зависимости от угла между сторонами котлована
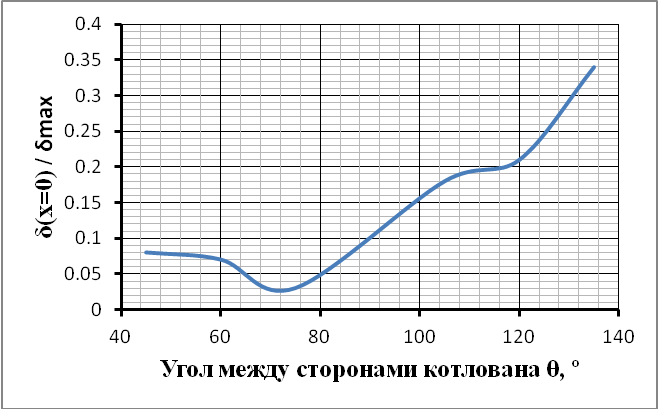
Рис. 8. Фактор №1 в зависимости от угла между сторонами котлована
По результатам анализа результатов расчетов (рис. 6) в формулу (1) введен поправочный коэффициент β, учитывающий влияния угла между смежными стенами на PSR. В результате чего формулы (1) и (3) примут следующий вид:
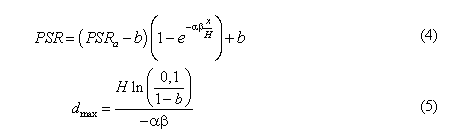
где β - коэффициент, учитывающий влияние величины угла между смежными стенками.
Графики, представленные на рис. 6, характеризуются следующим набором параметров функции (4)
Таблица 3
Параметры функции (4)
|
Угол между смежными стенами θ, º |
b, д.е. |
PSRa, д.е. |
β, д.е. |
|
45 |
0.075 |
0.93 |
1 |
|
60 |
0.075 |
0.95 |
1 |
|
75 |
0.03 |
0.96 |
1 |
|
90 |
0.1 |
1 |
1 |
|
105 |
0.18 |
0.97 |
1.1 |
|
120 |
0.21 |
0.97 |
1.3 |
|
135 |
0.34 |
0.97 |
1.4 |
По результатам регрессионного анализа данных, приведенных в таблице 3, получены зависимости для коэффициентов b и β (6), (7), представленные на рис. 9, 10 (где зеленым показаны графики функций (6), (7), красным – значения при углах θ от 45º до 90º, синим – значения при углах θ от 90º до 135º).
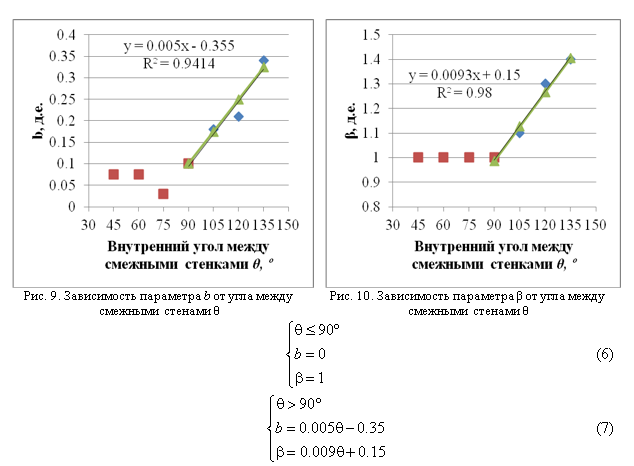
Из графиков (рис. 9, 10) видно, что при значениях угла между смежными стенами котлована θ менее 90 градусов параметр b принимает значения близкие к нулю, в то время как параметр β равен единице. При значении угла θ больше 90 градусов оба параметра имеют линейно возрастающую зависимость, описываемые уравнениями (7).
Влияния типа грунта, распорной системы и толщины ограждения котлована на угловой эффект
Для исследования влияния вида грунта, распорной системы и толщины ограждения котлована на угловой эффект, в ПК PLAXIS 3D была выполнена серия расчетов. В данных расчетах моделировалась откопка котлована до глубины 10 м с размерами котлована в плане 60 х 60 м. Ограждающая конструкция котлована – стена в грунте высотой 15 м. Распорная система котлована – два яруса распорок из стальных труб, установленных с шагом в плане 5 м. Последовательность устройства котлована для всей серии расчетов - не изменяется.
Принятые в расчетах характеристики грунта приведены в табл. 1, жесткости ограждения котлована и распорной системы представлены в табл. 5 и 6.
Таблица 5
Характеристики распорной системы
|
Вид распорки |
Material type |
Жесткость EA, МН |
Equivalent length, м |
|
Труба ø530х10 мм |
Elastic |
3267 |
10,0 |
|
Труба ø630х10 мм |
Elastic |
3895 |
10,0 |
|
Труба ø720х10 мм |
Elastic |
4595 |
10,0 |
Таблица 6
Характеристики ограждения котлована
|
Эквивалентная толщина элемента d, м |
Удельный вес плиты γ, кН/м3 |
Распределение свойств материала |
E1, МПа |
E2, МПа |
ν12 |
G12, МПа |
G13, МПа |
G23, МПа |
|
0,4 |
0,0 |
Изотропное |
30000 |
30000 |
0,2 |
12500 |
12500 |
12500 |
|
0,6 |
0,0 |
Изотропное |
30000 |
30000 |
0,2 |
12500 |
12500 |
12500 |
|
0,8 |
0,0 |
Изотропное |
30000 |
30000 |
0,2 |
12500 |
12500 |
12500 |
Эталонной для данной серии расчетов принята модель с параметрами:
- грунт: ИГЭ-1 песок средней крупности (см. табл. 1);
- распорная система: труба Æ 630х10 мм (см. табл. 5);
- ограждение котлована: толщиной d=0,6 м (см. табл. 6).
В ходе анализа результатов расчетов рассматривались перемещения ограждающей конструкции котлована, при изменении одного из параметров согласно таблицам 4, 5, 6.
Результаты расчетов перемещений ограждающей конструкции котлована при различных исследуемых параметрах в виде зависимостей нормализованных перемещений (δ(x) / δmax) от отношения расстояния от угла котлована к его глубине (x / H) представлены на рисунках 11 – 13 для половины подпорной стены ввиду симметрии.
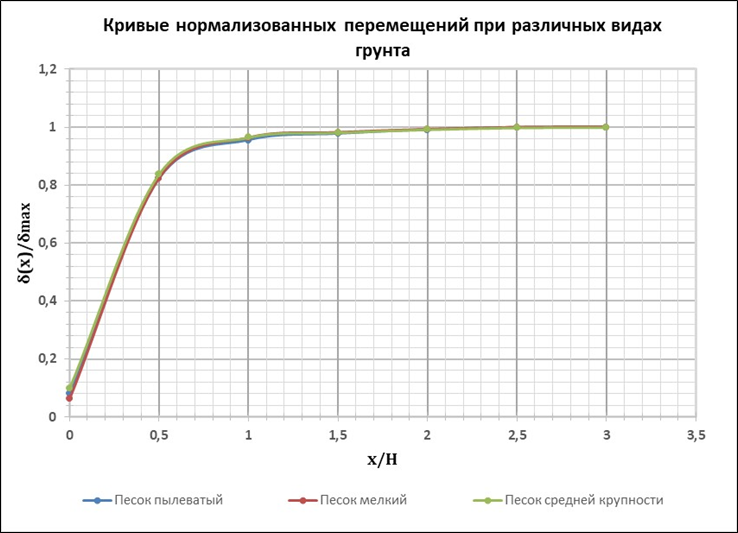
Рис. 11. Кривые нормализованных перемещений при различных видах грунта
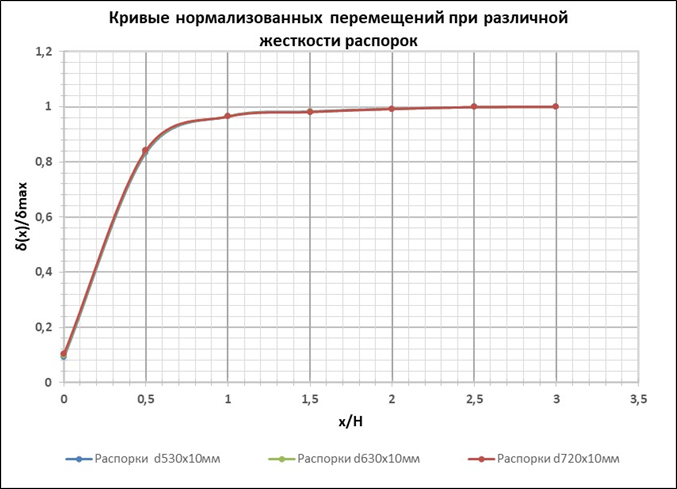
Рис. 12. Кривые нормализованных перемещений при различной жесткости распорок
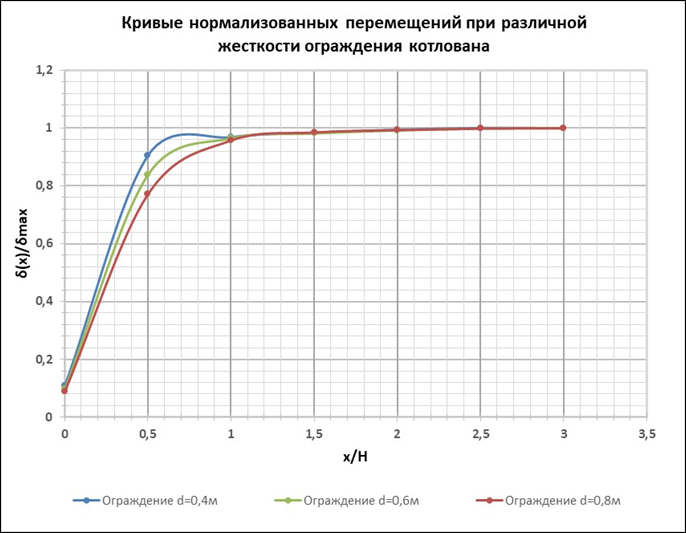
Рис. 13. Кривые нормализованных перемещений при различной жесткости ограждения котлована
Как видно из рисунков 11 – 13, изменение типа песчаного грунта и жесткости распорной системы не влияют на угловой эффект, а увеличение жесткости ограждения котлована приводит к увеличению зоны распространения углового эффекта.
Для учета влияния жесткости (толщины) ограждения котлована на действие углового эффекта введем в формулы (4) и (5) дополнительный коэффициент η. Тогда получим:
По результатам расчетов определены значения коэффициента η при различной изгибной жесткости конструкции ограждения котлована, соответствующей толщинам 0,4 м, 0,6 м и 0,8 м (рис. 14).
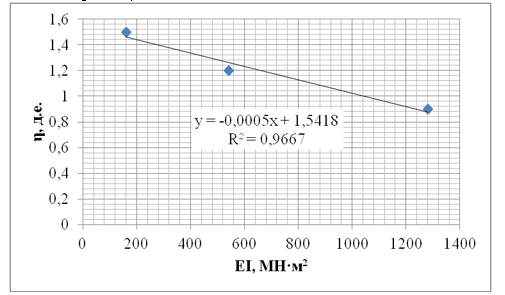
Рис. 14. Зависимость параметра η от изгибной жесткости ограждения
Как видно из рисунка 14, зависимость коэффициента η достаточно хорошо описывается линейным уравнением:
Методика расчета горизонтальных перемещений конструкции ограждения котлована в угловой зоне
На основании проведенных исследований можно рекомендовать следующую методику расчета конструкции ограждения в угловой зоне котлована, основанную на результатах расчетов в плоской постановке.
На первом этапе выполняется расчет перемещений конструкции ограждения котлована в плоской постановке, например, программном комплексе PLAXIS 2D.
Далее определяется внутренний угол между смежными стенами конструкции ограждения котлована θ, градус, и изгибная жесткость стены в грунте EI, МН·м2.
Из уравнений (2), (6), (7) и (10) определяются значения коэффициентов a, b, β и η.
По формуле (9) определяется размер зоны углового эффекта.
Расчет горизонтальных перемещений конструкции ограждения котлована в зоне действия углового эффекта производится по следующей зависимости:
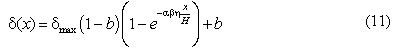
3. Заключение
В результате проведенных исследований установлено следующее.
- Горизонтальные перемещения конструкции ограждения снижаются по мере приближения рассматриваемого сечения к углам котлована в результате действия углового эффекта. Логично предположить, что вследствие этого снижаются усилия в конструкциях ограждения котлована и распорной системы, а также перемещения окружающего массива грунта.
- Получена эмпирическая зависимость, связывающая между собой перемещения конструкции ограждения котлована в угловых зонах с перемещениями, определяемыми при расчетах в плоской постановке.
- Размер зоны действия углового эффекта в плане зависит, в первую очередь, от глубины котлована. Также на величину зоны действия углового эффекта и характер распределения горизонтальных перемещений ограждения котлована оказывают влияние ее изгибная жесткость и угол между смежными стенами конструкции ограждения.
- Размер зоны действия углового эффекта и характер распределения горизонтальных перемещений конструкции ограждения котлована не зависит от жесткости распорной системы и физико-механических свойств песчаных грунтов основания.
- Дальнейшие исследования предполагается направить на уточнение методики по результатам численных исследований с использованием модели упрочняющегося грунта при малых деформациях (HSS), а также на определение зависимостей перемещений массива грунта в районе угловых зон котлованов для возможности выполнения расчетов оценки влияния устройства глубоких выработок на здания и сооружения окружающей застройки.
1. Pospechov V.S., Shulyatyev O.A., Baukov A.U., 2020. Corner effect study of the retaining wall design of an experimental excavation in sandy soils // Geotechnics, Vol. XII, № 1/2020 pp. 16-30. https://doi.org/10.25296/2221-5514-2020-12-1-16-30.
2. Petrukhin V.P., Pospechov V.S., Shulyatyev O.A., 2008. Deep excavation design and monitoring experience // Collection of scientific works NIIOSP named after N. M. Gersevanov, ed. 99, pp. 139-148.
3. Shulyatyev O.A., Mozgachyova O.A., Pospechov V.S. Underground urban space development: Science edition.-M.: Edition ASV, 2017.-510 p.
4. Bono N., Liu T., Soydemir C., 1992. Performance of an internally braced slurry-diaphragm wall for excavation support. In STP1129-EB Slurry Walls: Design, Construction, and Quality Control, in D. Paul, R. Davidson, N. Cavalli (eds), pp. 347-360. West Conshohocken, PA: ASTM International. DOIhttps://doi.org/10.1520/stp1129-eb.
5. Chew S.H., Yong K.Y., Lim A.Y.K., 1997. Three-dimensional finite element analysis of a strutted excavation // Computer Methods and Advances in Geomechanics, Vol. 3, pp. 1915-1920.
6. Faheem H., Cai F., Ugai K., 2004. Three-dimensional base stability of rectangular excavations in soft soils using FEM // Computers and Geotechnics, Vol. 31, No. 2, pp. 67-74. https://doi.org/10.1016/j.compgeo.2004.02.005
7. Finno R.J., Blackburn J.T., Roboski J.F., 2007. Three-dimensional effects for supported excavations in clay // Journal of Geotechnical and Geoenvironmental Engineering, Vol. 133, No. 1, pp. 30-36. DOI:https://doi.org/10.1061/(ASCE)1090-0241(2007)133:1(30).
8. Finno R.J., Bryson L.S., 2002. Response of a building adjacent to stiff excavation support system in soft clay // Journal of Performance of Constructed Facilities, Vol. 16, No. 1, pp. 10-20. DOIhttps://doi.org/10.1061/(ASCE)0887-3828(2002)16:1(10).
9. Fuentes R., 2018. Influence of corners in excavations on damage assessment // Geotechnical Research, Vol. 6, No. 2, pp. 1-12. https://doi.org/10.1680/jgere.18.00017.
10. Fuentes R., Devriendt M., 2010. Ground movements around corners of excavations: empirical calculation method // Journal of Geotechnical and Geoenvironmental Engineering, Vol. 136, No. 10, pp. 1414-1424. https://doi.org/10.1061/(ASCE)GT.1943-5606.0000347.
11. Hsiung B.Ch.B., Dao S.D., 2015. Impacts from three-dimensional effect on the wall deflection induced by a deep excavation in Kaohsiung, Taiwan // Proceedings of the 15th Asian regional Conference on soil mechanics and geotechnical engineering, 2015, pp. 1602-1607. http://doi.org/10.3208/jgssp.TWN-15.
12. Hsiung B.C.B., Yang K.H., Aila W., Ge L., 2018. Evaluation of the wall deflections of a deep excavation in Central Jakarta using three-dimensional modeling // Tunnelling and Underground Space Technology, No. 72, pp. 84-96. https://doi.org/10.1016/j.tust.2017.11.013.
13. Lee F.H., Yong K.Y., Quan K.C., Chee K.T., 1998. Effect of comers in strutted excavations: field monitoring and case histories // Journal of Geotechnical and Geoenvironmental Engineering, Vol. 124, No. 4, pp. 339-349.
14. Lin D.G., Woo S.M., 2007. Three dimensional analyses of deep excavation in Taipei 101 construction project // Journal of Geoengineering, Vol. 2, No. 1, pp. 29-41.
15. Moormann C., Katzenbach R., 2002. Three dimensional effects of deep excavations with rectangular shape // Planning and Engineering for the Cities of Tomorrow, Proceedings of the 2nd International Conference on soil structure interaction in urban civil engineering, Zürich, Switzerland, 2002, pp. 135-142.
16. Ou C.Y., Chiou D.C., 1993. Three-dimensional finite element analysis of deep excavation // Proceedings of 11th Southeast Asian Geotechnical Conference, Kuala Lampur, Malaysia, 1993, pp. 769-774.
17. Ou Ch.Y., Chiou D.Ch., Wu T.Sh., 1996. Three-dimensional finite element analysis of deep excavations // Journal of Geotechnical Engineering, Vol. 122, No. 5, pp. 337-345. DOIhttps://doi.org/10.1061/(ASCE)0733-9410(1996)122:5(337).
18. Ou C.Y., Shiau B.Y., Wang I.W., 2000. Three-dimensional deformationbehavior of the Taipei National Enterprise Center (TNEC) excavation case history // Canadian Geotechnical Journal, Vol. 37, No. 2, pp. 438-448.
19. Petrukhin V.P., Shuljatjev O.A., Pospekhov V.S., 2015. Design of a deep excavation retaining structure in congested urban environment in Moscow city // Proceedings of the XVI European Conference on Soil Mechanics and Geotechnical Engineering, Edinburgh, UK, 2015, pp. 4167-4172.
20. Takagi N., Shimamura K., Nishio N., 1984. Buried pipe responses to adjacent ground movements associated with tunneling and excavations // Proceedings of the 3rd International Conference on ground movements and structures, Cardiff, UK, 1984, pp. 97-113.
21. Tan Y., Wei B., Diao Y., Spatial X.Z., 2014. Spatial corner effects of long and narrow multipropped deep excavations in shanghai soft clay // Journal of Performance of Constructed Facilities, Vol. 28, pp. 04014015-1 - 04014015-17.
22. Wong L.W., Patron B.C., 1993. Settlements induced by deep excavations in Taipei. Proceedings of the 11th Southeast Asian geotechnical Conference, Singapore, 1993, pp. 787-791.
23. Roboski J.F., 2004. Three-dimensional performance and analyses of deep excavations: dissertation submitted to the graduate school in partial fulfillment of the requirements for the degree doctor of philosophy field of civil and environmental engineering. - Illinois, December 2004. - 256 p.
24. Roboski J., Finno R.J. Distributions of ground movements parallel to deep excavations in clay // Canadian Geotechnical Journal. Vol. 43. No. 1. - 2006, pp. 43-58. DOI:https://doi.org/10.1139/T05-091.
25. Zapata-Medina D.G. Semi-empirical method for designing excavation support systems based on deformation control: thesis submitted in partial fulfillment of the requirements for the degree of Masters of Science in Civil Engineering in the College of Engineering at the University of Kentucky: 25.07.07. - Kentucky. - 2007.
