employee from 01.01.2003 until now
Donskoy gosudarstvennyy tehnicheskiy universitet (Soprotivlenie materialov, docent)
employee
Don State Technical University (Strength of materials, associate professor)
employee
Rostov-na-Donu, Rostov-on-Don, Russian Federation
employee
employee
Rostov na Donu, Rostov-on-Don, Russian Federation
BBK 308 Монтаж, эксплуатация, ремонт машин и промышленного оборудования
One of the main directions in the application of fractal geometry is to create complex objects using simple algorithms using computer technology. The use of fractal geometry methods and the theory of deterministic chaos to describe real systems, in particular, in the development of the architectural appearance of the city, will allow solving problems of research and forecasting the development of the urban environment.
randomnicity, object, structure, form, structure, architecture, fractal, self-similarity
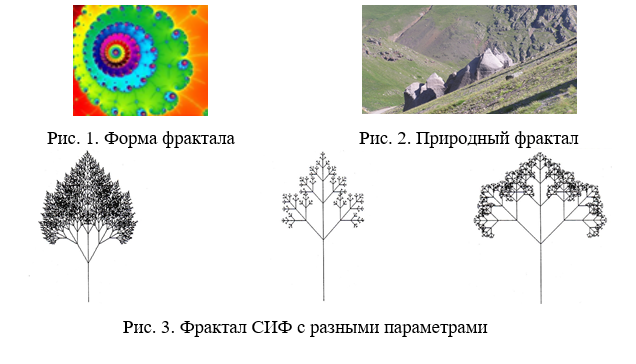
Фрактальная геометрия изучает закономерности, которые обладают фрагментарностью, изломанностью линий, нечеткостью границ и дробной размерностью [1-8]. Термин «фрактал» ввел в 1975 году Бенуа Мандельброт. Фракталы можно разделить на несколько видов: геометрические, алгебраические, стохастические и системы итеративных функций, для которых существует следующая классификация: системы IFS (Iterated Function Systems) и L-системы (рис. 1-3). Основная идея L-системы – это способ получения сложных объектов путем замены частей начального элемента по определенным правилам.
В современной науке фракталы применяются для моделирования сложных динамических систем. Фрактальные структуры представляют собой описание хаотичных процессов в динамических системах. В теории детерминированного хаоса, разработанной Бенуа Мандельбротом, существует важный факт, который состоит в том, что «динамическая система может быть абсолютно детерминистской, но не обнаруживать управления этой системой» [9]. Она может проявляться через хаотические формы, но они не случайны.
Есть случайность, а есть стихийная случайность. Именно введение понятия стихийной случайности в динамику систем и определяет теорию динамического хаоса [10-13]. Фрактальность природных форм и искусственно созданных архитектурных объектов выявляет детерминацию стихийной случайности.
Итак, динамические системы – это детерминированный хаос. Хаос подразумевает бесконечный, случайный процесс, когда его невозможно предсказать. Детерминированный хаос опирается на фрактальность объектов и процессов. Просто он означает другой порядок, другую структуру, более сложную, но обладающую более тонкой детерминационной структурой. Детерминированный хаос создается динамикой нелинейной системы со своими законами существования [14, 15].
Фрактальность означает изменчивость, почти одинаковую на всех уровнях рассматриваемой структуры. При динамическом порядке и хаосе наблюдается дисимметрия и скейлинг. Если первое понятие означает взаимопроникновение симметрии и асимметрии, то второе – это подобие со скольжением. Самоподобие – это процесс, в котором часть объекта, определенным образом в соответствии с дробной размерностью, т.е. увеличенная или уменьшенная, накладывается на весь объект, создавая совершенно новую структуру. Как известно, пространство вначале предполагалось только линейным (Евклидова геометрия), затем нелинейным или искривленным (геометрия Лобачевского Н.И. и теория А.Эйнштейна), то открытие фрактальной геометрии Б. Мандельбротом предполагает, что пространство и линейно, и нелинейно, и является фрактальным. Теория детерминированного хаоса Мандельброта описывает поведение нелинейных структур. За открытия в области фрактальной геометрии и теории детерминированного хаоса он был удостоен премии Вольфа в 1993 году.
Задать фрактальную структуру – значит задать принцип построения формы и структуры с учетом изменения и роста. Многообразие этих структур основывается на принципе единства в многообразие, который является основным для понимания мира и окружающей нас среды. Фракталы, постоянно изменяясь, способны создавать все новые, самые разнообразные формы из заранее заданной начальной структуры. В этом преимущества фрактального метода. Фракталы имеют две стороны – это динамические системы, способные к развитию и изменению, и они способствуют к созданию целого из фрагментов, где последующий элемент основан на развитии предыдущего, но уже на другом уровне.
Фрактальные алгоритмы нашли применение и в сфере информационных технологий. Фрактальная геометрия и теория детерминированного хаоса – это революция в изменении взгляда на мир, его преобразовании, в создании окружающей человека среды с учетом его комфортного проживания.
Фрактальный подход – это способ анализа и проектирования архитектурных форм, которые существенно обогатили бы современную архитектуру [16-20]. На рис. 4 показан архитектурный облик современного города.
Фрактальную архитектуру можно разделить на два типа: искусственно созданную, которая бывает интуитивной и сознательной, и естественно сложившуюся. Принципы фракталоподобного формообразования применяются при строительстве как отдельных объектов с фрагментами и деталями, так и в пространстве города в целом. Архитекторы прошлого широко использовали принцип фрактального строения. Элементы зданий порой являлись самоподобными объектами.
Рис. 4. Архитектурный облик Лондона.
В мире множество структур подчиняются фрактальным правилам построения и широко распространено в архитектуре, например, архитекторы использовали подобие частей целому, создавая цельный образ из отдельных элементов. Фрактальность архитектурных форм присуща многим объектам прошлого и настоящего времени (рис. 5 и 6).
Антонио Гауди создавал уникальные сооружения (Саграда Фамилия, Каса-Мила, Каса-Батльо, церковь колонии Гуэль, погреба, павильоны и дворец Гуэля, портал Миральеса, дом Кальвет и Эль-Каприччо), где фракталоподобные формы представлены хаотическими нерегулярными фракталами, которые похожи на природные объекты [21]. На рис. 7 и 8 показаны здания А. Гауди с фрактальными элементами.
Проведем сравнительный фрактальный анализ ключевых элементов данного сооружения в различных дробных размерностях. Он включает следующие этапы: определение фрактальной размерности объекта; расчет согласованности уровня фрактальности каждых элементов, входящих в рассматриваемый объект и на третьем этапе проводится согласование архитектурных деталей между объектами сооружения. Многоступенчатый фрактальный анализ здания или памятника архитектуры позволяет понять особенности проектирования объекта, его уникальность.
Город представляет собой фрактальное пространство, состоящее из зданий комплексов сооружений, транспортной сети (рис. 9 и 10).В это пространство входят как исторические здания, так и современные сооружения. Архитектура этих объектов в той или иной степени имеет фрактальный характер. Наиболее очевидной является геометрическая фрактальность, когда один и тот же элемент повторяется на разных уровнях.
Город – это пространственный и концептуальный мультифрактал стохастического типа. Так концентрическая застройка исторического центра Москвы или линейно-квадратная планировка Нью-Йорка представляет собой пространственный фрактал, который имеет повторяющийся алгоритм построения. Безусловно, в организации этого пространства имеются случайные изменения, но они в целом не влияют на общую структуру города.
Архитекторы заметили, что человек испытывает стресс, если находится среди бетонных зданий в виде прямоугольных пространственных объектов, где нет ни природных, ни архитектурных фрактальных элементов (рис. 11). И начинает чувствовать лучше в окружении природы или исторических зданий, при строительстве которых архитекторы интуитивно применяли самые разнообразные самоподобные элементы (рис. 12). Это относится к храмам, мечетям, дворцам, сооружениям бионической и зеленной архитектуры [22-27].
Для гармоничного развития городской среды необходимо проводить комплексные исследования и с учетом фрактальности самого пространства города. Фрактальный анализ в современных исследованиях широко применяется для изучения динамических систем. В мире были проведены исследования учеными М. Бэтти, П. Лохгли [28], а также Ле Корбюзье, Ф.Л. Райта, Заха Хадид и П. Франкхозер, развивая целое архитектурное направление – «фрактальная урбанистика».
Иногда архитекторы используют довольно формальный способ разнообразия городской застройки – делают визуальный акцент в виде высотных зданий и других деталей, которые только вносят диссонанс в архитектурный облик города. Нужно проводить комплексный анализ архитектуры города, учитывая все аспекты его развития. Фрактальная геометрия и теория детерминированного хаоса являются теми методами с помощью которых можно прогнозировать дальнейшее развитие архитектурного проектирования. Города будущего будут построены на принципах архитектурной бионики и зеленного строительства [22,23,26,27].
Город – это динамическая система, обладающая фрактальными свойствами, которые нельзя не учитывать при формировании городской среды и проектировании новых комплексов сооружений. Фрактальные городские пространства создаются естественно (исторически сложившиеся) и искусственно (по плану развития архитектурного облика города). Это два направления взаимнопересекаются, так как мало городов, которые стали строить с нуля по плану (рис. 13). И задача архитекторов гармонично вписывать современные здания в исторический облик города (рис. 14) [29-32].
При составлении прогноза развития городской среды можно использовать методы исследования теории детерминированного хаоса Мандельброта. До появления планов застройки городов архитектура развивалась, создавались удивительные по своей красоте и форме сооружения. Город – это динамическая система, которая развивается по своим законам, которые сложились исторически, этнографически и согласно культурным традициям в определенной природной среде. А динамические системы – это детерминированный хаос. Если при хаосе процесс носит случайный непредсказуемый характер, то при детерминированном хаосе – фрактальный характер, при этом процессы и объекты имеют более сложную структуру и другой уровень восприятия. В рассматриваемой структуре формообразования архитектуры города также наблюдается дисимметрия (единство симметрии и асимметрии) и скейлинг (изменяющееся самоподобие).
С появлением плана застройки городов городская среда не перестала быть динамической системой, хотя имеет больше рычагов управления. План развития города необходимо составлять на основе прогноза с использованием методов математического моделирования для динамических систем, учитывая всю сложность структуры, введением самых разнообразных и порой неожиданных векторов развития.
Фрактальные алгоритмы с помощью современной компьютерной графики позволяют визуализировать самые сложные объекты, в том числе пространство городской среды с отдельными сооружениями и их архитектурными элементами, с комплексами зданий, с транспортной инфраструктурой. Но хочется, чтобы возможности математического моделирования позволяли учитывать культурные, экологические, социальные аспекты развития города. С помощью методов теории детерминированного хаоса, начало которой положил Б. Мандельброт, можно учитывать механизмы, способные к самоорганизации и саморазвитию, что может привести к проектированию комплексов городских сооружений на новом уровне качества жизни в городской среде с учетом комфорта и экологичности [33].
Компьютерное моделирование, используя алгоритмы для архитектурного формообразования, дает возможность исследовать закономерности как архитектурного объекта, так и архитектурного облика города.
Необходимо понимать, что на данный момент математические методы фрактальной геометрии и теории детерминированного хаоса не могут смоделировать реальную динамическую систему, основанную на учете всех конкретных параметров заданной структуры, а лишь сделать прогноз развития системы города. Но математические методы и компьютерные технологии развиваются довольно интенсивно, и в будущем вполне возможно сделать более точную модель развития городской среды с учетом самых разных направлений на основе фрактальной геометрии и теории детерминированного хаоса.
1. Mandelbrot B. Fractal geometry of nature. - M.: Institute for Computer Research, 2002.- 656 p.
2. Morozov A.D. Introduction to the theory of fractals. - Nizhny Novgorod: Publishing House of Nizhny Novgorod University,, 2004. - 160 p.
3. Bozhochin S.V., Parshin D.A. Fractals and multifractals. - Izhevsk: SRC "Regular and Chaotic Dynamics", 2001. -128 p.
4. Barnsley M.F. Fractal everywhere. -New-York, Academic Press,1988. -394 p.
5. Mayatskaya I.A., Medvedeva T.A. Mathematical modeling of plant objects using elements of fractal geometry. // System analysis, management and information processing. Proceedings of the VII International Seminar, 2016, pp.44-49.
6. Mayatskaya I.A., Eremin V.D. Fractality of natural objects. // Actual problems of science and technology: Materials of the National. scientific-practical Conf., Rostov-on-Don, 2019 / Don. state tech. un-t (DSTU). - Rostov-on-Don, 2019. - pp. 704-705.
7. Mayatskaya I.A., Aslanyan A.R. Fractals around us. // Actual problems of science and technology: Materials of the National. scientific-practical Conf., Rostov-on-Don, 2020 / Don. state tech. un-t (DSTU). - Rostov-on-Don, 2020. - pp. 1693-1695.
8. Peitgen H.-O., Richter P.Kh. The beauty of fractals. Images of complex dynamical systems. -M.: Mir, 1993. - 176 p.
9. Mandelbrot B. Fractals, randomness and finance. - Moscow-Izhevsk: SRC "Regular and Chaotic Dynamics", 2004. - 256 p.
10. Kronover R.M. Fractals and chaos in dynamical systems. - M.: Technosphere, 2006. - 488 p.
11. Schroeder M.Fractals, chaos, power laws. Miniatures from endless paradise. - Izhevsk: SRC "Regular and Chaotic Dynamics", 2001. - 528 p.
12. Ruel D.Randomness and chaos. - Izhevsk: SRC "Regular and Chaotic Dynamics", 2001. - 192 p.
13. Prigogine I., Stengers I. Order from chaos: a new dialogue between man and nature. -M.: Progress, 1986. - 432 p.
14. Shuster G.Deterministic chaos: An introduction. -M.: Mir, 1988. -174 p.
15. Grinchenko V.T. Matsypura V.T., Snarskiy A.A.An Introduction to Nonlinear Dynamics: Chaos and Fractals. -M.: Publishing house of LCI, 2010. -280 p.
16. Mayatskaya I.A., Yazieva S.B. Fractality in architecture.// Actual problems of science and technology: Materials of the National. scientific-practical Conf., Rostov-on-Don, 2019 / Don. state tech. un-t (DSTU). - Rostov-on-Don, 2019. - pp. 705-708.
17. Mayatskaya I.A., Belovolov M.G. The use of fractal surfaces in the design of structures.// Actual problems of science and technology: Materials of the National. scientific-practical Conf., Rostov-on-Don, 2020 / Don. state tech. un-t (DSTU). - Rostov-on-Don,, 2020. - pp. 1695-1697
18. Yazyev B.M., Mayatskaya I.A., Yazyeva S.B., Yazyev S.B. Fractality in architectural forms and in organization of space in buildings // IOP Conf. Series: Materials Science and Engineering. - 2019. - №698. CATPID-2019, 022087
19. Mayatskaya I.A., Yazyeva S.B., Kashina I.V., Nesterova A.N. The manifestation of fractality in the architecture of buildings and Structures // IOP Conf. Series: Materials Science and Engineering. - 2019. - №698. CATPID-2019, 033046
20. Mayatskaya I.A., Yazyeva S.B., Yazyev B.M. Fractality and symmetry in architectural elements of buildings. // Construction and technological safety, 2018. № 12 (64), pp. 29-32.
21. Hensbergen G.V. Gaudi is the bullfighter of art. -M.: Eksmo-Press,2002. -358 p.
22. Mayatskaya I.A., Yazyev B.M., Yazyeva S.B., Kulinich P.B. Building Constructions : architecture and nature, //MATEC Web of Conferences. - 2017. - №106. SPbWOSCE-2016, 01031
23. Mayatskaya I.A., Eremin V.D., Yazieva S.B. Green architecture: the unity of the beauty of nature, comfort, environmental friendliness and architectural forms. // Construction and architecture, 2019. T. 7. № 1. pp. 91-96.
24. Mayatskaya I.A., Yazyeva S.B.,Zakieva N.I.,Lapina A.P Modern glass constructions and comfortable urban environment //Materials Science Forum, Vol.931. pp. 754-758
25. Mayatskaya I.A., Yazyeva S.B., Kolotienko M.A., Yazyev B.M. The use of glass structures in the design of unique structures // IOP Conf. Series: Materials Science and Engineering. - 2019. - №698. CATPID-2019, 022083
26. Eremin V.D., Avdeeva A.G. Modern trends in the design of environmentally friendly houses. // Experimental and theoretical research in the XXI century: problems and development prospects: materials of the XIV All-Russia. scientific-practical Conf., Rostov-on-Don, 2018 / South. un-t IUBiP. - Rostov-on-Don, 2018.- pp. 95-98
27. Mayatskaya I.A., Eremin V.D., Turtogtokh Bat-Erdene. Architectural bionics: past and present. // Materials Science Forum "Scientific Research of the SCO countries: synergy and integration", Beijing, China, April 8-9, 2019 . - Beijing, 2019. - P. 116-124
28. Batty M., Longley P. Fractal Cities: a geometry of form and function. -San Diego, Academic Press,1994. -394 p.
29. Kushner M. The future of architecture. 100 most unusual buildings. - M.: AST, 2016. - 176 p.
30. Trube G. Guide to architectural forms. - M.: Architecture - S, 2014. - 216 p.
31. Gnedich P.P. World architecture. - M.: Eksmo-Press, 2012. -240 p.
32. Dobritsina I.A.From postmodernism to non-linear architecture. -M.: Progress- tradition, 2004. - 416 p.
33. Iovlev V.I. Architectural space and ecology. - Yekaterinburg: Architecton, 2006 -297 p.
