Moscow, Russian Federation
The article is devoted to mathematical modeling of flow distribution in hydraulic net-works. Calculations of hydraulic networks are carried out at the stage of their design and operation. The results of numerical simulation are used to control the operation of the hy-draulic network in real time. The mathematical model of the distribution of flows in the hydraulic network is a system of nonlinear equations. The nodal pressures method used to solve the system of equations numerically is the n-dimensional Newton method. To ensure stable and fast convergence of the iterative process, it is proposed to use the initial approx-imation taking into account the network topology and parameters of its objects, use the lower relaxation factor and optimize the structure of the Maxwell matrix. The algorithms presented in the paper allow one to significantly reduce the dimension of the system of nonlinear equations being solved.
hydraulic network, nodal pressure method, band matrix, equivalenting
Введение
Основные положения теории гидравлических сетей были заложены В.Я. Хасилевым и А.П. Меренковым в шестидесятые годы прошлого века. Их идеи развиваются в работах их соратников и учеников. Исторически для решения задачи распределения потоков в гидравлических сетях предпочтение отдавалось методу контурных расходов (МКР). Даже для полностью разомкнутых сетей контуры создавались искусственно. Бесспорным преимуществом МКР перед методом узловых давлений (МУД) является значительно меньшая размерность системы уравнений. В МКР размерность равна количеству главных контуров, в МУД – количеству узлов с неизвестными давлениями. Преимуществом МУД перед МКР является то, что метод позволяет моделировать работу гидравлической сети любой конфигурации (с контурами, без контуров, с любым количеством узлов с заданным давлением) без дополнительного искусственного зацикливания сети.
Переход на «умные» технологии требует моделирования работы гидравлических сетей в реальном времени. Это означает, что пользователь должен иметь возможность оперативно изменять режим эксплуатации сетью (открывать/закрывать запорные устройства, переключать насосы, подключать/отключать дополнительные источники и т.д.) и быстро получать результаты моделирования. Эти задачи равноценны по значимости. Первая задача – разработка интерфейса. Пользователь готов затратить много времени и сил на сбор и первичный ввод информации, но при этом корректировать данные оперативно. Вторая задача – собственно моделирование работы гидравлической сети. Основное требование - быстродействие для моделирования сетей реальных размеров. В статье рассматривается только вторая задача.
Methods
При известной топологии и параметрах гидравлической сети ее математическая модель строится на основании законов Кирхгофа:
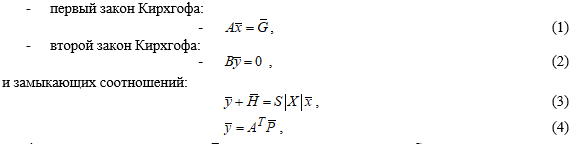
где A – матрица инцидентности; В – матрица главных контуров; S – диагональная матрица сопротивлений связей; |X| - диагональная матрица расходов на участках; ![]() - вектор расходов в узлах;
- вектор расходов в узлах; ![]() - вектор действующих напоров на участках;
- вектор действующих напоров на участках; ![]() - вектор расходов на участках;
- вектор расходов на участках; ![]() - вектор разностей давлений на участках;
- вектор разностей давлений на участках; ![]() - вектор давлений в узлах.
- вектор давлений в узлах.
После упрощения системы уравнений (1-4) узловая система уравнений приобретает вид:
![]()
Итерационный процесс строится с использованием формулы:

матрица Максвелла, вычисленная при текущем векторе расходов ![]() - невязка в узле.
- невязка в узле.
Метод узловых давлений – это метод Ньютона, который, как известно, имеет высокую скорость сходимости только в окрестности точки решения. Выбор начального приближения для итерационного процесса очень важен. Рекомендации по решению этой проблемы не существуют.
Для поиска начального приближения к решению системы уравнений (5-6) предлагается заменить зависимость (6) на линейную зависимость:
![]()
Тогда начальное приближение ![]() может быть найдено в результате решения системы линейных уравнений:
может быть найдено в результате решения системы линейных уравнений:
![]()
где ![]() матрица Максвелла, вычисленная при
матрица Максвелла, вычисленная при ![]()
Таким образом, при вычислении начального приближения используется вся имеющаяся информация о топологии сети и текущих параметрах объектов. Не смотря на это, в некоторых случаях скорость сходимости не достаточно высока. Для обеспечения стабильной монотонной сходимости в формулу (7) вводят релаксационный множитель ![]() , значение которого вычисляют на каждом шаге итерации. Такой подход существенно увеличивает время, затрачиваемое на одну итерацию. В теоретически обосновывается, что для положительно определенного Якобиана, для обеспечения монотонной сходимости достаточно выбирать
, значение которого вычисляют на каждом шаге итерации. Такой подход существенно увеличивает время, затрачиваемое на одну итерацию. В теоретически обосновывается, что для положительно определенного Якобиана, для обеспечения монотонной сходимости достаточно выбирать ![]() <1. Практический опыт автора позволил установить следующий ряд значений
<1. Практический опыт автора позволил установить следующий ряд значений ![]() =0,5 для k < 6,
=0,5 для k < 6, ![]() = 0,6 для k < 8,
= 0,6 для k < 8, ![]() = 0,7 для k < 10,
= 0,7 для k < 10, ![]() =1 для
=1 для ![]() . Данный подход обеспечивает сходимость процесса за максимум 15 итераций.
. Данный подход обеспечивает сходимость процесса за максимум 15 итераций.
На каждом шаге итерации необходимо решать систему линейных уравнений или обращать матрицу (8). По своей структуре матрица Максвелла (8) совпадает с матрицей смежности, которая для графов, моделирующих гидравлические сети, является разреженной. Для уменьшения времени, затрачиваемого на одну итерацию, узлы графа переномеровываются в соответствии с алгоритмом, что позволяет привести матрицу к ленточной форме с минимальной шириной ленты. Следующий шаг в оптимизации времени расчета – использование метода Холецкого для решения систем линейных уравнений с положительно определенными ленточными матрицами.
Размерность решаемых задач стала такой большой, что предложенных способов оптимизации времени расчета уже не достаточно. В работах предлагаются разные способы уменьшения размерности решаемой задачи, одни из них не вносят дополнительной погрешности в результаты, другие способы вносят минимальную погрешность. В работах излагается идея упрощения задачи, но алгоритмы ее решения не приводятся.
При разработке алгоритмов важна организация данных. В описанных ниже алгоритмах информация о топологии сети хранится в двумерном массиве, каждая строка которого соответствует участку сети, а столбцы содержат номера узлов, инцидентных участку.
В процессе эксплуатации гидравлической сети происходит перекрытие задвижек. В результате чего, некоторые части сети могут оказаться отключенными от источника. Выявление подобных ситуаций необходимо делать автоматически.
Высокоуровневое описание алгоритма выявления множества узлов, связанных с источником, представлено ниже.
Connectivity_checkg – выделение узлов сети, связанных с источником (выявление связных компонент графа сети).
- Маркировать узел «Источник».
- Кол-во_маркированных_узлов = 1.
- Повторять пока Кол-во_маркированных_ узлов >0:
- Кол-во_маркированных_ узлов = 0
- Для каждого участка:
- Найти участок, у которого маркирован один из инцидентных ему узлов;
- Маркировать смежный узел;
- Кол-во_маркированных_ узлов увеличить на 1.
В дальнейшем в расчетах рассматриваются только узлы, связанные с источником.
На втором этапе происходит поиск и удаление из рассмотрения ненагруженных деревьев. Под ненагруженным деревом понимается граф, не имеющий циклов, для узлов которого вектор G=0. Высокоуровневое описание алгоритма представлено ниже.
Unloaded_trees - поиск ненагруженных деревьев.
search for unloaded trees
- Вычислить валентность всех узлов графа.
- Кол-во_маркированных_связей = 1.
- Повторять пока Кол-во_маркированных_связей >0:
- Кол-во_маркированных_ связей = 0
- Для каждого немаркированного участка:
- Если валентность одного из инцидентных связи узлов равна 1, он не имеет нагрузки и не является источником, то:
- валентность узлов, инцидентных связи, уменьшить на 1;
- связь маркировать;
- Кол-во_маркированных_связей увеличить 1.
Дальнейшее упрощение расчетной схемы происходит за счет вычленения и удаления нагруженных деревьев из графа сети. Процесс начинается с терминальных узлов. В результате определяются расходы на всех участках и нагрузка корневого узла, которая увеличивается на суммарную нагрузку всех узлов, вошедших в дерево (рисунок 1). Индексы всех узлов и связей, вошедших в нагруженные деревья, равны 1. После того, как найдено давление в корневом узле, находятся давления во всех узлах, принадлежащих дереву (модуль Unfurl). Высокоуровневое описание алгоритмов представлено ниже.
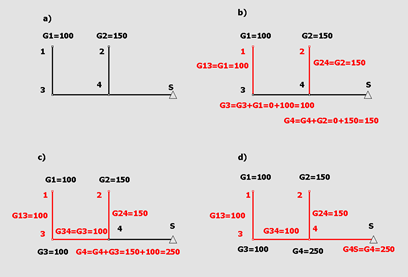
Рисунок 1 Последовательность эквивалентирования нагруженных деревьев гидравлической сети a) – исходное состояние сети; b) перенос нагрузки в узлы 3 и 4; отсекаемые узлы - 1 и 2; c) перенос нагрузки в узел 4; отсекаемый узел 3; d) перенос нагрузки в узел S; отсекаемый узел 4.
Furl – скручивание нагруженных деревьев.
- Вычислить валентность всех узлов графа.
- Кол-во_маркированных_связей = 1.
- Повторять пока Кол-во_маркированных_связей >0:
- Кол-во_маркированных_связей = 0
- Для каждой немаркированной связи j (i;k):
- Если валентность одного из инцидентных связи узлов равна 1, и он не является источником, то:
- Валентность обоих узлов уменьшить на 1;
- Связь маркировать;
- Присвоить индексу узла I значение 1;
- Кол-во_маркированных_связей увеличить на 1;
- Если отсекаемый узел – конец связи (k), то:
- присвоить значению расхода значение нагрузки отсекаемого узла
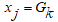
- увеличить значение нагрузки смежного узла на значение нагрузки отсекаемого узла
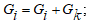
- Если отсекаемый узел – начало связи (i), то:
- присвоить значению расхода инверсное значение нагрузки отсекаемого узла
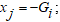
- уменьшить значение нагрузки смежного узла на значение нагрузки отсекаемого узла
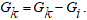
Unfurl – раскручивание свернутых нагруженных деревьев.
Кол-во_маркированных_связей = 1.
- Повторять пока Кол-во_маркированных_связей >0:
- Кол-во_маркированных_связей = 0.
- Для каждой немаркированной связи j (i;k) , принадлежащей дереву:
- Если индекс одного из инцидентных связи узлов равен 1 и он не маркирован, то:
- Вычислить давление в смежном узле по формуле:
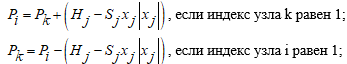
- Маркировать смежный узел;
- Присвоить значение 1 индексу связи;
- Связь маркировать;
- Кол-во_маркированных_связей увеличить на 1.
Эффективность применения модуля Furl зависит от типа сети и решаемой задачи. Например, наладочный расчет систем теплоснабжения производится при заданной тепловой нагрузке абонентов, которая пересчитывается в расчетные расходы теплоносителя. В этом случае большую часть сети, а в некоторых случаях и всю сеть, удается «свернуть».
Графы, моделирующие расчетные схемы гидравлических сетей, могут содержать большое количество последовательных и параллельных связей. Эквивалентирование таких связей позволяет существенно уменьшить размерность решаемой системы уравнений.
Последовательные ребра – ребра, инцидентные одному и тому же узлу, который не имеет нагрузки, степень которого равна 2. При замене двух последовательных связей одной (рисунок 2 a-b) на единицу уменьшается количество узлов и добавляется новая связь. Гидравлическое сопротивление новой связи равно сумме сопротивлений замененных связей.
Параллельными связями называются связи, у которых совпадают пары инцидентных им узлов. Порядок перечисления узлов в паре не имеет значения. При замене двух параллельных связей одной не меняется количество узлов и добавляется новая связь, гидравлическая проводимость которой равно сумме проводимостей замененных связей, соединяющая те же концевые узлы (рисунок 2 c-d).
Процесс упрощения схемы начинается с поиска и эквивалентирования последовательных связей, затем происходит поиск и эквивалентирование параллельных связей, затем снова поиск последовательных связей, затем параллельных и так до тех пор, пока не останется последовательных и параллельных связей. Связи, инцидентные узлам, моделирующим насосы или регуляторы не эквивалентируются.
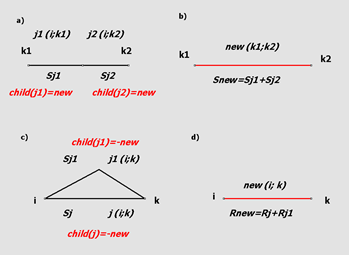
Рисунок 2 Эквивалентирование связей сети. a-b) последовательное соединение; c-d) параллельное соединение; a, c ) - исходное состояние; b-d) результат эквивалентирования.
Обратный ход состоит в присвоении значений расходов дочерних связей значениям расходов родительских связей (последовательные связи) и в вычислении значений расходов родительских связей (параллельные связи). Высокоуровневое описание алгоритмов представлено ниже.
Equivalenting_forward
- Вычислить валентность всех узлов графа.
- Определить количество узлов без нагрузки, валентность которых равна 2 (number_serial).
- Определить количество параллельных связей (number_parallel).
- Количество связей new=nl
- Повторять пока есть последовательные и параллельные связи (number_serial+ number_parallel>0):
- Если есть последовательные связи (number_serial>0), то
- Для каждой немаркированного узла i, валентность которого равна 2, и у которого отсутствует нагрузка:
- Найти 2 немаркированные связи j1 (i; k1) и j2 (i; k2), инцидентные узлу i;
- Маркировать найденные связи j1 и j2;
- Маркировать узел i;
- Создать новую связь new=new+1 (k1;k2);
- Вычислить гидравлическое сопротивление связи new по формуле Snew =Sj1+Sj2;
- Вычислить гидравлическую проводимость связи new Rnew=Snew-2;
- Сохранить номер связи new как дочерний subsidiary affiliate child
для связей j1 и j2.
- Определить количество параллельных связей (number_parallel).
- Если есть параллельные связи (number_parallel>0), то
- Для каждой немаркированной связи j (i; k):
- Найти параллельную ей немаркированную связь j1 (i; k);
- Маркировать найденные связи j и j1;
- Создать новый участок new=new+1 (i; k);
- Вычислить гидравлическую проводимость связи new по формуле Rnew =Rj+Rj1;
- Вычислить гидравлическое сопротивление связи new по формуле Snew = Rnew-0.5;
- Сохранить отрицательный номер связи new как дочерний для связей j и j1.
- Определить количество узлов без нагрузки, валентность которых равна 2 (number_serial).
Equivalenting_back
- Для каждого маркированной связи j, включая новые, начиная с большего номера с шагом -1:
- Найти узлы (i;k), инцидентные связи j;
- Вычислить
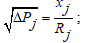 ;
; - Для каждой немаркированной связи j1, начиная с 1 до j:
- Найти узлы (i1;k1), инцидентные связи j1;
- Найти родительскую связь (по совпадению номера дочернего участка j1 c номером j);
- Если номер дочерней связи >0 (т.е. последовательное соединение), то вычислить расходы на родительских связях:
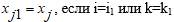 , и
, и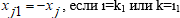 .
.
- Если номер дочерней связи <0 (т.е. параллельное соединение), то
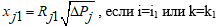 , и
, и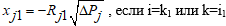 .
.
- Вычислить

- Маркировать связь.
Выводы
- Анализ состояния гидравлических сетей требует проведения расчетов в реальном времени. Этот факт повышает требования к надежности и быстродействию вычислительных процессов.
- Эквивалентные преобразования сети позволяют существенно уменьшить размерность систем нелинейных уравнений, а в отдельных случаях ликвидировать итерационный процесс, заменив его на последовательные вычисления.
- Использование в методе узловых давлений нижнего релаксационного множителя обеспечивает быструю и монотонную сходимость итерационного процесса.
Приведение матрицы Максвелла к ленточной форме и оптимизация ширины позволяют сократить время проведения одной итерации.
1. Merenkov A P and Khasilev V Ya 1985 Theory of hydraulic circuits (Moscow: Nauka) p 294
2. Novitsky N N, Shalaginova Z I and Mikhailovsky 2017 Object-oriented models of heat supply system thermal point elements Vestnik IrGTU 21(9) 157-72
3. Shalaginova Z I, Novitsky N N, Tokarev V V and Grebneva O A 2015 Multilevel modeling of thermohydraulic regimes of large heat supply systems. Energy of Russia in the XXI century. Innovative Development and Management Irkutsk 389-98
4. Kitaytseva E Kh 1995 Generalized methods for calculating the air regime of buildings and factors affecting the quality of internal air. Abstract of the candidate of technical sciences (Moscow: MGSU) p 18
5. Ortega J M and Rheinboldt W C 1975 Iterative solution of nonlinear equations in several variables (Moscow: Mir) p 558
6. Ortiga J, Bruno J C, Coronas A and Grossman I E 2007 Review of optimization models for the design of polygeneration systems in district heating and cooling networks 17th European symposium on Computer Aided Process Engineering ESCAPE 17 Elsevier
7. Swamy M N and Thulasiraman K 1984 Graphs, Networks and Algorithms (Moscow: Mir) p 455
8. Tewarson R P 1977 Sparce matrices (Moscow: Mir) p 189
9. Wilkinson J H and Reinsch C 1976 Handbook for automatic computation Linear Algebra (Moscow: Mashinostroyeniye) p 389
10. Loginov K V 2004 Equivalenting hydraulic circuits for modeling large areas of heating networks Mathematical structures and modeling 13 62-71
11. Yakshin S V 2018 Application of graph splittance method when optimizing heating network parameters Vestnik IrGTU 22(10) 129-40
12. Schcherbakov V I and Nguyen H C 2016 The energy equivalence principle for calculation of water supply networks with many areas Vestnik RUDN 4 27-34
13. Yakshin S V 2017 The method of graph splitting and the principle of heating network additivity Vestnik IrGTU 21(4) 127-38
14. Sidorova V T and Karchin V V 2016 Power flow redistribution in 10 kV complex closed-circuit air networks to reduce losses and improve power quality J Energy Prob 11 51-4
15. Todini E and PIlati S 2003A gradient algorithm for the analysis of pipe network computer applications in water supply (London: John Wiley & Sons) 1 1-20
16. Wang Jinda, ZhouZhigang and Zhau Jianing 2016 A method for the steady-state thermal simulation of district heating systems and model parameters calibration Energy Conversion and Management 120 294-305
17. Mauna Kuosa, Kaisa Kontu, Tapio Makila, Markku Lampinen and Risto Lahdelma 2013 Static study of traditional and ring networks and use of mass flow control in district heating applications Applied Thermal Engineering 54(2) 450-9
18. Lipovka A Y and Lipovka Y L 2013 Application of “Gradient” algorithm to modeling thermal pipeline networks with pumping stations J Siberian Federal Universit Engineering and Technologies 6 28-35



















