employee
Rostov-na-Donu, Rostov-on-Don, Russian Federation
employee
Rostov-na-Donu, Rostov-on-Don, Russian Federation
Russian Federation
Don State Technical University (student)
GRNTI 67.23 Архитектурно-строительное проектирование
GRNTI 67.01 Общие вопросы строительства
OKSO 270000 АРХИТЕКТУРА И СТРОИТЕЛЬСТВО
BBK 385 Строительные конструкции
BBK 308 Монтаж, эксплуатация, ремонт машин и промышленного оборудования
TBK 5414 Строительные конструкции
The study of the membrane coating of large-span structures is carried out. Five stages of installation and operation of the coating are considered. The uneven snow pressure on the coating was calculated and applied to the finite element model of the structure. Based on the results, the authors also provide conclusions and summary about the considered structure. Two options of emergency cases have been investigated. The results showed that the support contour is a key element of the structure. The failure of any element, connection except of the support contour does not lead to plastic deformations in the coating.
large-span building, survivability, erection sequence, finite element method, finite element model, stress-strain state
В современной практике проектирования актуальна проблема безопасности при эксплуатации строительных конструкций. Выполнение требований живучести конструктивных систем зданий и сооружений становится основной задачей строительной отрасли. Понятие живучести определяется как свойство системы полностью или частично выполнять свое функциональное назначение при локальном отказе составляющих элементов конструктивной схемы[1].
В качестве объекта исследования выбрано большепролетное покрытие. Наиболее рациональный вариант покрытия – мембранное, совмещающее в себе главные достоинства оболочек: объединение несущей и ограждающей функции при низкой металлоемкости. Безопасность принятого конструктивного решения гарантируется высокой надежностью и живучестью мембранных покрытий. Покрытие опирается на железобетонные колонны, связанные монолитными плитами со стальным опорным контуром.
При исследовании живучести покрытия достаточно выполнить моделирование отказа «ключевых» или наиболее нагруженных элементов[2]. В исследуемом покрытии «ключевые» элементы представлены в виде опорного контура и угловых ферм. На живучесть оказывает влияние несущая способность наиболее нагруженных элементов. Уровень живучести конструкции как неповрежденного покрытия, так и после повреждения, оценивается индексом живучести Inrob :
где Rmax,n – связность n-го уровня;
Rфакт,n – количество полученных повреждений на n-м этапе повреждений.
Выделены основные принципы и методики расчета мембранного покрытия на живучесть[3]:
– в дискретных конструктивных системах аварийное воздействие вызывается неумышленным отказом одного конструктивного элемента или узла;
– для моделирования отказа заменяют конечный элемент или узел граничными внутренними усилиями;
– в расчете учитываются нормативные постоянные и временные длительные нагружения;
– узлы сопряжений конечных элементов принимают равнопрочными основным элементам;
– сталь работает как упруго-пластичный материал, характеристики стали принимают с нормативными значениями;
– конструкция имеет высокую живучесть, когда разрушение какого-либо элемента и перераспределение усилий на другие элементы не приводит к разрушению конструкции.
Условие неразрушения элементов:
εmax ≤ γi · [εult], (2)
где εmax – максимальная деформация в сечении элемента;
[εult] – предельная деформация, при которой происходит разрыв;
γi – коэффициент запаса.
Нагружение системы выполняется с поэтапным увеличением нагрузки на каждой стадии монтажа[4]. Величина прироста нагрузки 
на i-ой стадии нагружения определялась по формуле:
где q - суммарная расчетная нагрузка на мембранное покрытие;
N - количество ступеней нагружения.
Для исследования живучести покрытия применен метод конечных элементов (МКЭ)[5]. Конечно-элементная модель каркаса сооружения создана в программном комплексе LIRA 10.8 в виде пространственной плитно-стержневой системы (Рис. 1).
Для монолитного железобетонного каркаса приняты плиты перекрытия толщиной 220 мм из бетона класса В5, диафрагмы жесткости 300 мм, сечение колонн 800x800 мм из бетона класса В30. Опорный контур выполнен из стального короба, угловые фермы – металлические, мембранное покрытие из металлического листа толщиной 4 мм, монтажные элементы «постели» проектируются в виде стальных полос сечением 300х6 мм с шагом 3 м.
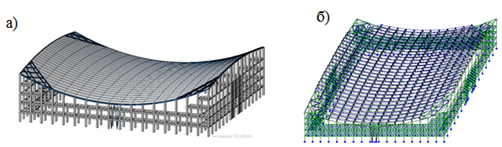
Рис.1. Расчетная модель сооружения: а) 3D вид; б) конечно-элементная модель
В расчетной модели учтен собственный вес элементов конструкций, снеговое и ветровые воздействия[6]. Расчет выполнен с учетом последовательности монтажа. Рассмотрены пять стадий: навеска монтажных элементов «постели»; раскладка листов мембраны; заварка мембраны; учет веса кровли; действие равномерной или неравномерной снеговой нагрузки.
Выполнен расчет с учетом этапности возведения и нагружения конструкций покрытия. На Рис. 2 показаны перемещения опорного контура и мембраны с уточнением значений результатов расчета за стадию и относительно начального положения[7].
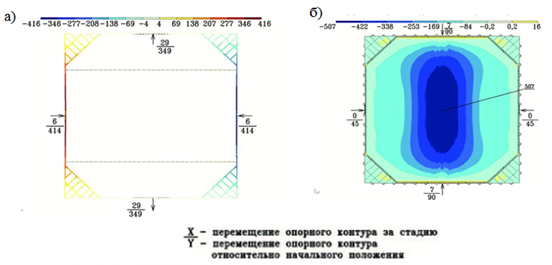
Рис. 2. Вертикальные перемещения: а) опорного контура, стадия 1;
б) опорного контура и мембраны, стадия 2
В результате расчета конструкций на третей и четвертой стадиях получены главные напряжения в конструкциях покрытия (Рис. 3).
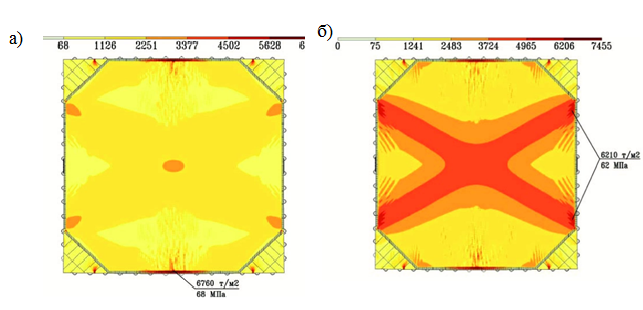
Рис. 3. Главные напряжения: а) стадия 3; б) стадия 4
На четвертой стадии выполнен анализ прироста моментов в мембранном покрытии. Максимальный крутящий момент в мембране составил 531 тс*м, в опорном контуре – 113 тс*м (Рис. 5).
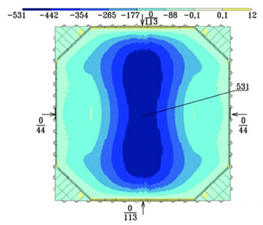
Рис 5. Изополя крутящего момента на 4 стадии этапности возведения
На пятой стадии расчета учтена работа конструкции покрытия при неравномерной снеговой нагрузке (Рис. 6).
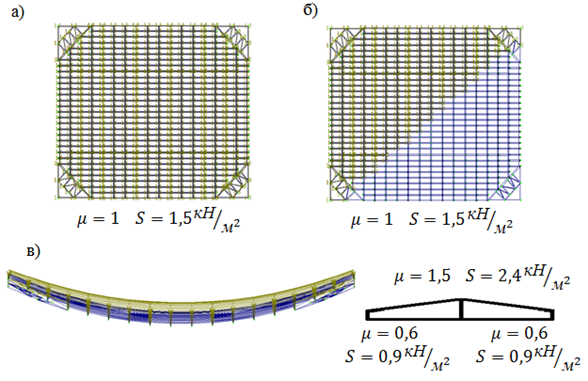
Рис 6. Варианты учета снеговой нагрузки: а) первый вариант; б) второй вариант; в) третий вариант
На Рис. 7. показаны изополя крутящих моментов и главных напряжений при учете неравномерной снеговой нагрузки.
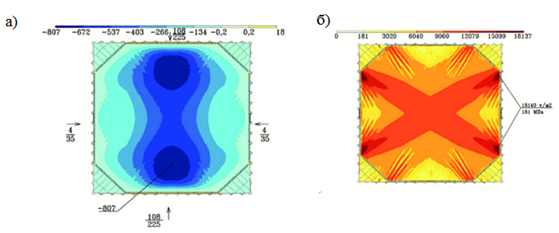
Рис. 7. Результаты расчета 5 этапа монтажа: а) крутящие моменты;
б) главные напряжения
Анализ результатов расчета показал, что каркас здания способен воспринимать горизонтальные и вертикальные воздействия, обеспечивать устойчивость при свободном перемещении опорного контура в направлении, ортогональном плоскости наружных стен. Мембрана активно работает в наиболее растянутом диагональном направлении. Наибольшие деформации мембраны возникают в зоне диагонального креста (Рис. 8)[8].
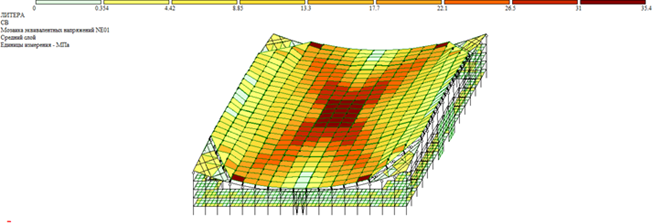
Рис. 8. Схема распределения главных напряжений
Выполнено моделирование двух аварийных ситуаций: разрез мембраны; обрушение узла сопряжения колонны и опорного контура[9]. Результаты расчета при первом варианте аварийной ситуации показан на Рис. 9.
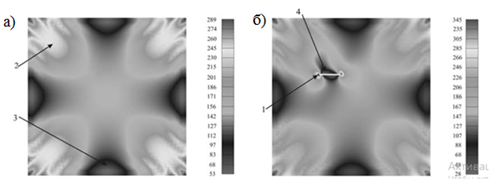
Рис. 9. Изополя приведенных напряжений: а) до разреза; б) после разреза
Схема вертикальных перемещений полотна мембраны после отказа элемента опорного контура приведена на Рис. 10.
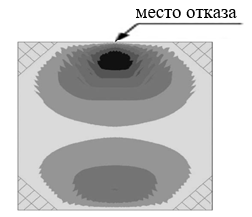
Рис. 10. Вертикальные перемещения полотна мембраны
При выводе одного узла из работы система не теряет геометрической неизменяемости, что говорит об изначально высоком потенциале живучести выбранной конструктивной схемы[10]. Исключение составит узел сопряжения опорного контура и угловых ферм, так как опорный контур одновременно является составляющей частью данных ферм, отказ элементов контура повлечет разрушение части покрытия, состоящего из фермы и элементов «постели». При этом оставшаяся часть покрытия сохраняет несущую способность конструкции, образуя две независимые системы.
Анализ результатов моделирования аварийных ситуаций показал, что мембранные покрытия обладают живучестью, обеспечивая надежность и безопасность конструктивных решений и рекомендуются при проектировании большепролетных сооружений.
1. Kudishin YU.I., Drobot D.YU. K voprosu o zhivuchesti stroitelnyh konstrukcij // Stroitelnaya mekhanika i raschet sooruzhenij. - 2008. - № 2 (217). - R. 36 - 43.
2. Kudishin YU.I., Kancheli N.V., Drobot D.YU. K ocenke bezopasnosti bolsheproletnyh membrannyh pokrytij // Stroitelnye materialy, oborudovanie, tekhnologii 21 veka. - 2008. - № 5 (112). RS. 30 - 33.
3. Eremeev P.G. Predotvrashchenie lavinoobraznogo (progressiruyushchego) obrusheniya nesushchih konstrukcij unikalnyh bolsheproletnyh sooruzhenij pri avarijnyh vozdejstviyah // Stroitelnaya mekhanika i raschet sooruzhenij. - 2006. - № 2. - p. 23-27.
4. Eremeev P.G. Osobennosti proektirovaniya unikalnyh bolsheproletnyh zdanij i sooruzhenij // Stroitelnaya mekhanika i raschet sooruzhenij. - 2005. - № 1. - p. 5-12.
5. Agahanov E.K., Agahanov M.K., Batmanov E.Z. The stress-strein state from its own weight in ground base with trapezoidal cutout. MATEC Web of Conferences. 193, 03047 (2018) https://doi.org/10.1051/matecconf/201819303047.
6. Agahanov E. K., Kravchenko G. M., Osadchij E.V., Trufanova E.V. Raschet zdanij slozhnoj geometricheskoj formy na vetrovye vozdejstviya. Vestnik Dagestanskogo gosudarstvennogo tekhnicheskogo universiteta. Tekhnicheskie nauki. - 2017. - № 2. - p. 8-17.
7. Kancheli N.V., Batov P.A., Drobot D.YU. Realizovannye membrannye obolochki: raschet, proektirovanie, vozvedenie. - M.: ASV. - 2009. - 110 p.
8. Agahanov E.K. O razvitii kompleksnyh metodov resheniya zadach mekhaniki deformiruemogo tverdogo tela. Vestnik Dagestanskogo gosudarstvennogo tekhnicheskogo universiteta. Tekhnicheskie nauki. - 2013. - № 2. - p. 39-45.
9. Kravchenko G., Trufanova E., Kostenko D., Tsurikov S. Analysis of blast load on a reinforced concrete column in the time domain // International Science Conference SPbWOSCE-2016 \"SMART City\".- 2017. - p. 04019.
10. Agahanov E.K., Kravchenko G.M., Trufanova E.V. Regulirovanie parametrov sobstvennyh kolebanij prostranstvennogo karkasa zdaniya // Vestnik Dagestanskogo gosudarstvennogo tekhnicheskogo universiteta. Tekhnicheskie nauki, - 2016. - № 3. - p. 8-15.
