from 01.01.1977 to 01.01.2023
Rostov-on-Don, Rostov-on-Don, Russian Federation
Rostov-na-Donu, Rostov-on-Don, Russian Federation
Rostov-on-Don, Russian Federation
Russian Federation
Russian Federation
CSCSTI 67.03
Russian Classification of Professions by Education 270000
Russian Library and Bibliographic Classification 308
The article deals with the simulation of joint work of slab grillage and monolithic frame of the building by finite element method. The finite-element model is developed in the spatial formulation according to the complex scheme "upper structure-base plate-pile Foundation". The pile field was modeled by pliable rods with stiffness corresponding to the average draft of the pile field. Static and dynamic calculations are performed in the ING+software package. The results of the stress-strain state of the building frame elements demonstrate the correctness of this approach to take into account the compliance of the base.
finite element method, finite element model, dynamic calculation, slab grillage, pile Foundation
При моделировании работы оснований зданий и сооружений используют следующие подходы: в первом проводится переход от пространственной задачи к двухмерной (плоская или осесиметричная деформация); во втором работу основания моделируют упрощенной моделью.
Простейшую модель Винклера-Фусса достаточно часто применяют в научных и инженерных расчетах. Модель обладает рядом недостатков, существенным из которых является невозможность учета взаимного влияния различных частей сооружения на основание. Аналогичными недостатками обладает двухпараметрическая модель Пастернака. В рассматриваемых моделях кинематические гипотезы вызывают определенные сомнения.
Для исследования совместной работы плитного ростверка и каркаса здания рассмотрен многоэтажный жилой дом с подземной автостоянкой в г.Таганроге. Подвальный этаж, в котором располагается автостоянка, разделен на две части деформационным швом. Первая надземная часть имеет офисный этаж, 16 жилых этажей и технический этаж. Покрытие второй части подвального этажа используется в качестве дворового пространства с возможностью заезда пожарных машин.
Конструктивная схема здания выполнена с несущим каркасом из монолитных железобетонных конструкций.
Фундаментная плита первой основной части здания толщиной 1500мм, второй - толщиной 600мм. Фундаментная плита основной части опирается на свайное поле, фундаментная плита второй части – на подготовленное естественное основание.
Основными несущими элементами каркаса здания являются монолитные колонны сечением 400х400, 500х500 и 600х600мм; монолитные диафрагмы жесткости толщиной 200мм, 300мм, 400мм; стены подвала - 400мм, 500мм; монолитные плиты перекрытий толщиной 200 и 250 мм. Все конструктивные элементы выполнены из бетона В25, арматура продольная класса А400, поперечная класса А240.
Стены подвального этажа одновременно воспринимают вертикальную нагрузку и нагрузку от обратной засыпки грунта.
Вертикальная нагрузка, действующая на плиты перекрытия и покрытия, распределяется за счет их жесткости на вертикальные элементы – колонны, несущие монолитные стены и диафрагмы жесткости. Горизонтальная ветровая нагрузка воспринимается в уровне плит перекрытий и перераспределяется на диафрагмы жесткости и ядра жесткости в лестнично-лифтовых узлах. Частично горизонтальная нагрузка влияет на перераспределение вертикальные усилия в колоннах и диафрагмах, которые за счет изменения вертикальных усилий также воспринимают часть ветрового момента. Фундаментная плита опирается на свайное основание по схеме высокого ростверка.
Пространственная жесткость и неизменяемость сооружения обеспечивается высокой степенью статической неопределимости, включением в совместную работу всех несущих конструктивных элементов. Стены подвального этажа жестко соединены с перекрытием.
Для решения поставленной задачи применен метод конечных элементов [1]. Существуют различные конечно-элементные комплексы, которые позволяют производить расчет сложных инженерных сооружений на статическое и динамическое воздействие.
В программных комплексах прочностного расчета используется метод конечных элементов в форме метода перемещений, построенный на основе вариационного принципа Лагранжа. Глобальная матрица жесткости ансамбля конечных элементов формируется из локальных матриц жесткости отдельных элементов путем их соединения в общих узлах. Затем учитываются граничные условия (условия опирания и сопряжения элементов). Вектор узловых сил системы строится по заданным внешним узловым воздействиям и распределенных по площади элемента или его граней нагрузок. Неизвестный вектор узловых перемещений определяется в процессе решения системы уравнений метода перемещений. Затем, для каждого конечного элемента, используя найденные узловые перемещения, определяют деформации, напряжения. По найденным напряжениям определяют интегральные усилия (изгибающие и крутящие моменты, продольные и поперечные усилия).
Расчет выполнен по лицензионной версии программы ING+, имеющим сертификат соответствия и верификацию программного комплекса РААСН.
Модель разработана в пространственной постановке по комплексной схеме «верхнее строение – фундаментая плита – свайное основание» (рис. 1а).
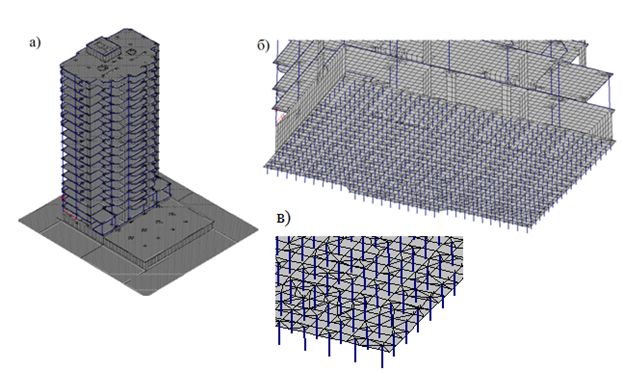
Рис. 1. – Конечно-элементная модель: а) общий вид;
б) плитный ростверк; в) фрагмент плитного ростверка
В работе при моделировании свайного поля предложено использовать податливые стержни с жесткостью, соответствующей средней осадке свайного основания (рис. 1б,в) [2-3].
Статический расчет выполнен на постоянную нагрузку от несущих и ненесущих конструкций, временную (полезную) и снеговую нагрузки. В конечно-элементную модель добавлены данные по статической ветровой нагрузке в различных направлениях.
Выполнен динамический расчет по определению спектра частот и форм собственных колебаний [4-6]. Для учета инерционных характеристик грунтового массива при решении спектральной задачи жесткость основания принята бесконечной. Спектр частот включает первые две формы – поступательные, третью – крутильную, что соответствует требованиям норм проектирования. Характерные формы колебаний в виде поступательной, крутильной и изгибно-крутильной приведены на рис. 2.
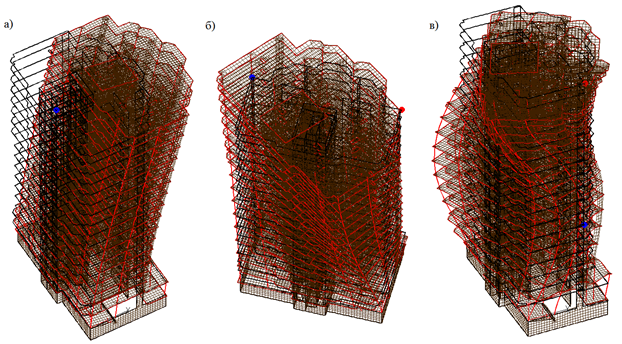
Рис. 2 – Характерные формы колебаний: а) поступательная; б) крутильная;
в) изгибно-крутильная
Для учета пульсационной составляющие ветровой нагрузки сформированы исходные данные, в соответствии с ветровым районом, геометрическими параметрами здания, типом местности и конструктивной схемой сооружения (рис. 3) [7-8].
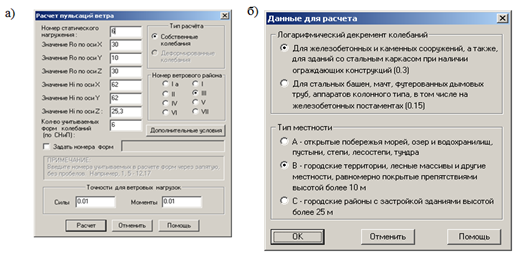
Рис. 3 - Параметры определения пульсационных нагружений:
а) основные; б) дополнительные условия
Выполнен статический расчет здания с учетом пульсационной составляющей ветровой нагрузки и определены деформации и усилия в элементах каркаса здания (рис. 4).
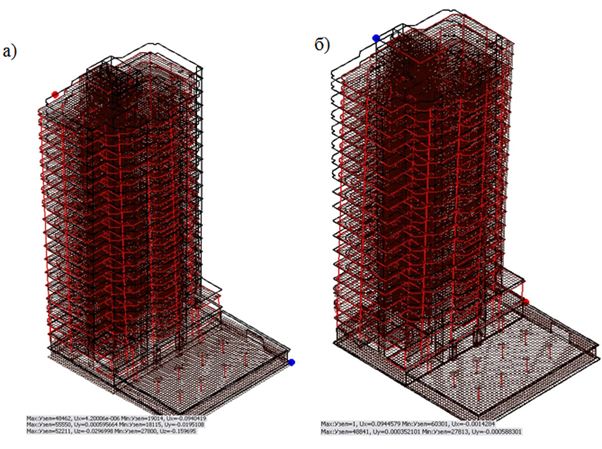
Рис. 4 - Деформации здания: а) от полной нормативной вертикальной нагрузки; б) от ветровой нагрузки с учетом пульсационной составляющей
Деформации фундаментной плиты от вертикальной нагрузки изменяются от 85 до 120мм. Неравномерность осадок 35мм. Здание имеет некоторый крен только от вертикальных нагрузок, обусловленный неравномерностью загружения плиты в плане. Максимальный крен верха здания составляет 94мм.
От действия ветра (с учетом пульсации) максимальные отклонения верха здания 95мм, что не превышает нормативно допустимых значений.
Выполнен анализ напряженно-деформированного состояния плитного ростверка (рис. 5).
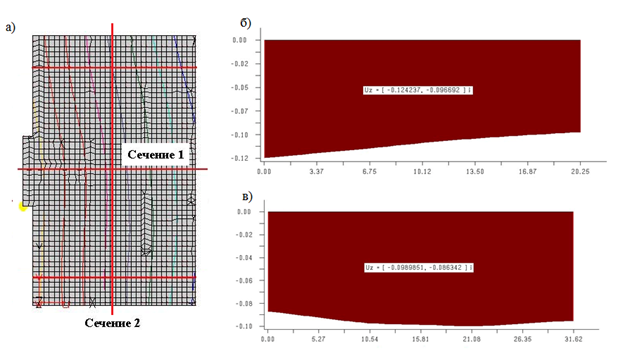
Рис. 5 – Плитный ростверк: а) маркировка сечений 1, 2; б) вертикальные перемещения в сечении 1; в) вертикальные перемещения в сечении 1
Деформации фундаментной плиты от вертикальной нагрузки изменяются от 85 до 120мм.
На рис. 6 показаны изгибающие моменты в плитном ростверке.
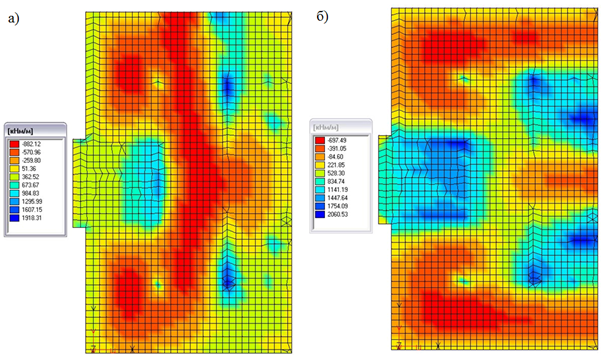
Рис. 6 – Изгибающие моменты в плитном ростверке: а) относительно оси Х;
б) относительно оси Y
По результатам напряженно-деформированного состояния плитного ростверка определено распределение верхней и нижней арматуры вдоль осей Х и Y (рис. 7.).
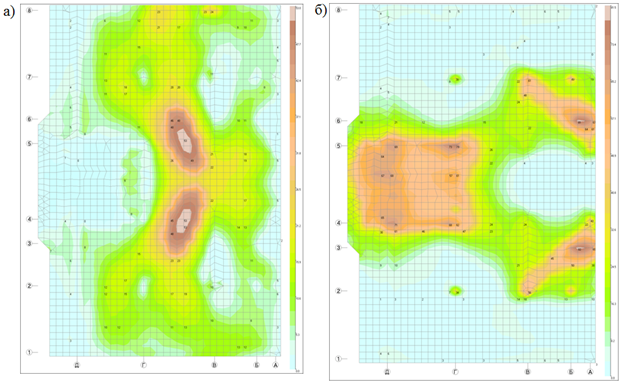
Рис. 7 – Армирование плитного ростверка: а) верхняя арматура вдоль оси Х;
б) нижняя арматура вдоль оси Y
Предлагаемый подход моделирования податливости свайного основания жесткими стержнями ростверка позволяет корректно определить изгибающие усилия и правильно рассчитать армирование фундаментной плиты, в то время как нормативная равномерная осадка свайного поля не учитывает эти усилия и неравномерные деформации.
1. Batht K.-J. Finite Element Procedures. K.-J. Batht//New Jersey: Prentice Hall, 1996. pp. 10-12.
2. Kravchenko G.M., Trufanova E.V., Nazarenko D.I., SHaripov EH.R. Raschet zdaniya obshchezhitiya tekhnoparka Rostovskogo gosudarstvennogo stroitel'nogo universiteta (RGSU) s primeneniem razlichnyh modelej osnovaniya // Inzhenernyj Vestnik Dona, №3, 2015 URL:ivdon.ru/ru/magazine/archive/n3y2015/3228.
3. Kadomcev M.I., Lyapin A.A., Timofeev S.I. K voprosam postroeniya ehffektivnyh algoritmov rascheta sistemy «sooruzhenie-grunt» // Inzhenernyj vestnik Dona, 2012, №1. URL: ivdon.ru/magazine/archive/n1y2012/719/
4. Kravchenko G.M., Trufanova E.V., SHutenko E. O., Hashkhozhev K. N. Dinamicheskij raschet ob"ekta «Sportivno-ozdorovitel'nyj kompleks» Tekhnoparka RGSU// Inzhenernyj vestnik Dona, №4 2015, URL: ivdon.ru/ru/magazine/archive/n4y2015/3279.
5. Zotova E. V., Panasyuk L. N. CHislennoe modelirovanie dinamicheskih sistem s bol'shim chislom stepenej svobody na impul'snye vozdejstviya // Inzhenernyj vestnik Dona, 2012, №3 URL: ivdon.ru/magazine/archive/n3y2012/933/
6. Agahanov EH.K., Kravchenko G.M., Trufanova E.V. Regulirovanie parametrov sobstvennyh kolebanij prostranstvennogo karkasa zdaniya // Vestnik Dagestanskogo gosudarstvennogo tekhnicheskogo universiteta. Tekhnicheskie nauki. 2016. T. 42. № 3. pp. 8-15.
7. Agahanov EH.K., Kravchenko G.M., Osadchij A.S., Trufanova E.V. Raschet zdanij slozhnoj geometricheskoj formy na vetrovye vozdejstviya. // Vestnik Dagestanskogo gosudarstvennogo tekhnicheskogo universiteta. Tekhnicheskie nauki. 2017. T. 44. № 2. pp. 8-17.
8. Kravchenko G.M., Trufanova E.V. Uchet pul'sacii vetra pri raschete zdanij s nesushchimi kirpichnymi stenami // Nauchnoe obozrenie. 2014. № 11-3. pp. 796-799.



















