Moscow, Russian Federation
Moskva, Moscow, Russian Federation
CSCSTI 67.11
CSCSTI 67.01
Russian Classification of Professions by Education 08.02.02
Russian Library and Bibliographic Classification 222
Russian Library and Bibliographic Classification 30
Russian Library and Bibliographic Classification 38
Russian Library and Bibliographic Classification 385
Russian Library and Bibliographic Classification 308
Russian Trade and Bibliographic Classification 50
Russian Trade and Bibliographic Classification 5014
Russian Trade and Bibliographic Classification 54
Russian Trade and Bibliographic Classification 5414
Ferma s odnoy nepodvizhnoy sharnirnoy i tremya podvizhnymi oporami imeet dvoynuyu krestoobraznuyu reshetchatuyu strukturu. Vyvodyatsya analiticheskie zavisimosti progiba ot chisla paneley. Uravneniya dlya opredeleniya usiliy v sterzhnyah reshayutsya v simvol'noy forme v sisteme komp'yuternoy matematiki Maple. Primenyaetsya formula Maksvella - Mora i metod indukcii dlya polucheniya obschego resheniya.
Ferma, progib, formula Maksvella- Mora, Maple
Расчет перемещений узлов фермы, необходимый для оценки ее деформативности, обычно выполняют численно в одном из стандартных пакетов. С увеличением числа стержней в ферме увеличивается и размер матрицы уравнений равновесия узлов. Начиная с некоторого значения, любой численный метод начинает давать погрешности, недопустимые, если речь идет о таких ответственных расчетах, как расчеты мостов, покрытий промышленных сооружений, концертных залов, стадионов. Именно в таких сооружениях как правило применяются фермы с большим числом панелей. В работах [1-3] показано, что для многих статически определимых стержневых регулярных (с периодической решеткой) ферм возможно получить формульное решение, свободное от упомянутого "проклятия размерности". Аналитические решения для пространственных [4-10] и плоских ферм [11-19] получены с использованием системы компьютерной математики Maple и метода индукции. В настоящей работе на основе программы [20] для нахождения усилий в стержнях статически определимых фермах и упомянутого метода индукции выводятся формулы для прогиба центрального узла плоской фермы (рис. 1). Ферма с n панелями (считаются по нижнему поясу) содержит m=4n+18 стержней и 2n+9 сочленяющих узлов. Ферма статически определима, однако из трех уравнений равновесия конструкции в целом (как это обычно делается в начале расчета) найти пять реакций не удается. Это связано с тем, что ферма без опор не является жестким телом и имеет две степени свободы. Отсюда неизбежно применения полного расчета фермы вырезанием всех узлов и составление общей системы равновесия.
1. Рассмотрим решение задачи о действии сосредоточенной силы. В программу [20] вводятся координаты узлов, порядок соединения стержней и узлов. Результатом расчетов являются аналитические выражения для усилий. Смещение вычисляется по формуле Максвелла – Мора
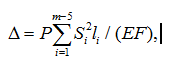
где — усилия в стержнях фермы от действия единичной нагрузки P,
— длины стержней, EF — жесткость стержней (принята одинаковой для всех стержней). Принимается четное число панелей n=2k. Суммирование ведется по всем стержням, кроме опорных. В процессе счета было замечено, что при k=2,5,8... определитель системы уравнений равновесия обращается в ноль. Для того, чтобы исключить эти значения из метода индукции для параметра k выбирается закон изменения
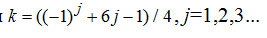

Рис.1. Ферма при значениях
Получено следующее выражение для прогиба
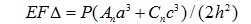 (1)
(1)
где 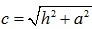 . Методом индукции найдены коэффициенты
. Методом индукции найдены коэффициенты
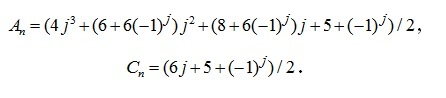
Для этого из решений для ферм с числом панелей от 1 до 14 были выявлены последовательности коэффициентов перед кубами линейных размеров a и c соответственно:

Оператор rgf_findrecur из пакета genfunc системы Maple по этим данным дал рекуррентные уравнения, которым удовлетворяют члены последовательностей:
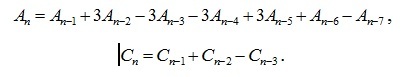
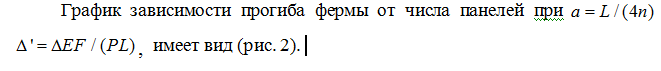
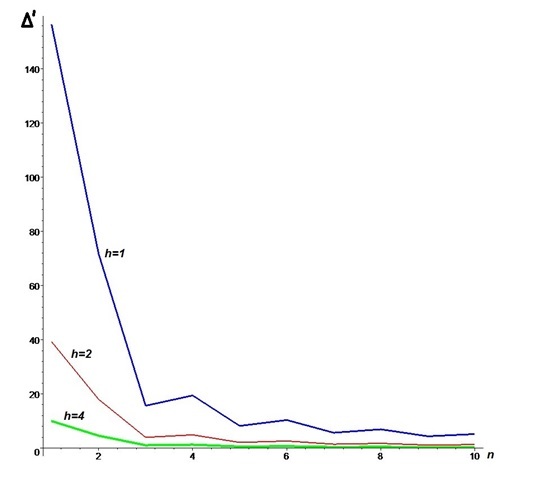
Рис.2. График зависимости прогиба фермы от числа панелей, L=100м
Одновременно с выводом формулы для прогиба можно получить и формулы для расчета реакции опоры стержней. Горизонтальная компонента реакции неподвижной опоры: . Вертикальные реакции подвижных опор:
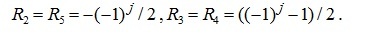
2. Рассчитаем в (1) коэффициенты от распределенной нагрузки ( рис.3).
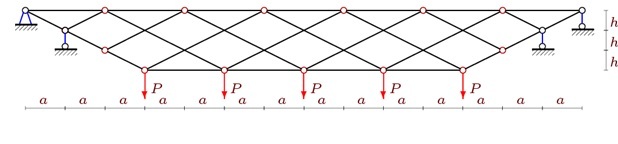
Рис.3. Ферма с распределенной нагрузкой
Методом индукции получено
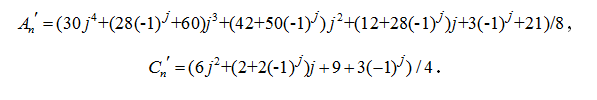
Для этого из решений для ферм с числом панелей от 1 до 18 были выявлены последовательности коэффициентов перед кубами линейных размеров a и c соответственно:
7, 207, 399, 1871, 2811, 7683, 10315, 21771, 27423, 49703, 60087, 98487, 115699, 176571, 203091, 293843, 332535, 461631
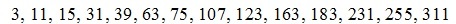
Оператор rgf_findrecur из пакета genfunc системы Maple по этим данным дал рекуррентные уравнения, которым удовлетворяют члены последовательностей:
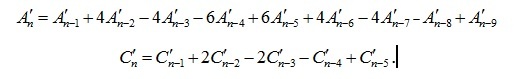 .
.
1. Hutchinson R. G., Fleck N.A. Microarchitectured cellular solids - the hunt for statically determinate periodic trusses // ZAMM Z. Angew. Math. Mech. 2005. 85, No. 9, Pp. 607-617.
2. Hutchinson R.G., Fleck N.A. The structural performance of the periodic truss // Journal of the Mechanics and Physics of Solids. 2006. Vol. 54. No. 4. Pp. 756-782.
3. Zok F. W., Latture R. M., Begley M. R. Periodic truss structures // Journal of the Mechanics and Physics of Solids. 2016. vol. 96. Pp. 184-203. https://doi.org/10.1016/j.jmps.2016.07.007
4. Kirsanov M. N. Stress State and Deformation of a Rectangular Spatial Rod Cover // Scientific Herald of the Voronezh State University of Architecture and Civil Engineering. Construction and Architecture. 2016. Vol. 31. No. 3. Pp. 71-79.
5. Kirsanov M. N. Analysis of the buckling of spatial truss with cross lattice // Magazine of Civil Engineering. 2016. No. 4. Pp. 52 - 58. DOI:https://doi.org/10.5862/MCE.64.5
6. Kirsanov M.N. Analiticheskoe issledovanie zhestkosti prostranstvennoy staticheski opredelimoy fermy // Vestnik MGSU. 2017. T. 12. Vyp. 2 (101). S. 165-171.
7. Kirsanov M.N., Andreevskaya T.M. Analiz vliyaniya uprugih deformaciy machty na pozicionirovanie antennogo i radiolokacionnogo oborudovaniya // Inzhenerno-stroitel'nyy zhurnal. 2013. №5(40). S. 52-58.
8. Kirsanov M.N. Izgib, kruchenie i asimptoticheskiy analiz prostranstvennoy sterzhnevoy konsoli // Inzhenerno-stroitel'nyy zhurnal. 2014. № 5 (49). S. 37-43.
9. Kirsanov M.N. Raschet prostranstvennoy sterzhnevoy sistemy, dopuskayuschey mgnovennuyu izmenyaemost' // Stroitel'naya mehanika i raschet sooruzheniy. 2012. № 3. S. 48-51.
10. Voropai R. A., Kirsanov M.N. On the deformation of spatial cantilever trusses under the action of lateral loads // Science Almanac. 2016. No. 9-2(23). S.17-20. DOI:https://doi.org/10.17117/na.2016.09.02.017
11. Domanov E. V. Analiticheskaya zavisimost' progiba prostranstvennoy konsoli treugol'nogo profilya ot chisla paneley//Nauchnyy al'manah. 2016. №6-2 (19). S. 214-217. DOI:https://doi.org/10.17117/na.2016.06.02.214
12. Ershov L.A Formuly dlya rascheta deformaciy piramidal'nogo kupola // Nauchnyy al'manah. 2016. № 11-2(25). S. 315-318. DOI:https://doi.org/10.17117/na.2016.11.02.315
13. Tinkov D. V., Safonov A. A. Design Optimization of Truss Bridge Structures of Composite Materials // Journal of Machinery Manufacture and Reliability. 2017. Vol. 46, No. 1, Pp. 46-52. DOI:https://doi.org/10.3103/S1052618817010149
14. Astahov S.V. Vyvod formuly dlya progiba vneshne staticheski neopredelimoy ploskoy fermy pod deystviem nagruzki v seredine proleta// Stroitel'stvo i arhitektura. 2017. T. 5. № 2. S. 50-54.
15. Kirsanov M.N., Suvorov A.P. Issledovanie deformaciy ploskoy vneshne staticheski neopredelimoy fermy // Vestnik MGSU. 2017. T. 12. Vyp. 8 (107). S. 869-875. DOI:https://doi.org/10.22227/1997-0935.2017.8.869-875
16. Kirsanov M.N. Analiz progiba arochnoy fermy // Stroitel'naya mehanika inzhenernyh konstrukciy i sooruzheniy. 2017. - № 5. - S. 50-55
17. Kirsanov M. N. Analiz usiliy i deformaciy v korabel'nom shpangoute modeliruemogo fermoy // Vestnik Gosudarstvennogo universiteta morskogo i rechnogo flota imeni admirala S. O. Makarova. - 2017. - T. 9. - № 3. - S. 560-569. DOI:https://doi.org/10.21821/2309-5180-2017-9-3-560-569
18. Kirsanov M.N., Zaborskaya N.V. Deformations of the periodic truss with diagonal lattice // Magazine of Civil Engineering. 2017. No. 3. Pp. 61-67. doi:https://doi.org/10.18720/MCE.71.7.).
19. Belyankin N.A., Boyko A. Y. Analysis of the deflection of the flat statically determinate girder // Sciense Almanac. 2017. N 2-3(28). S. 246-249. https://elibrary.ru/download/elibrary_28913792_32626016.pdf
20. Kirsanov M.N. Maple i Maplet. Resheniya zadach mehaniki. SPb.: Izd-vo Lan', 2012. 512 s.


















