с 01.01.2019 по настоящее время
Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова (Общеинженерные дисциплины, профессор)
с 01.01.1980 по 01.01.2019
г. Москва и Московская область, Россия
Москва, г. Москва и Московская область, Россия
Изложены теоретические и материалы для создания аналого-дискретных моделей рельефа местности и их использования при решении инженерных задач. С их помощью возможно моделирование - областей затопления, расчет поступления солнечной радиации, планирование строительства объектов инфраструктуры и других задач. Рассмотрены различные варианты трактовки построения аналитических и дискретных моделей рельефа местности. Приведены блочные модули алгоритмов построения, обработки и визуализации аналоговых моделей рельефа. Приведены выборки структурированных источников данных для их создания. Предложена методика моделирования рельефа, основанная на использовании логико-математических и матричных методов обработки больших данных.
Локальная система координат, рельеф местности, средне-планировочная поверхность, аналитическая модель рельефа, векторизация, аппроксимация
Введение
Модульная алгоритмизация аналитических зависимостей цифровых моделей территорий – средство аналитико-цифрового представления трехмерных пространственных объектов поверхностей или рельефов в виде массивов данных, образующих множество высотных отметок, отметок глубин и иных значений аппликат, — координаты Z локальной системы координат (ЛСК) в узлах регулярной или нерегулярной сети. Или совокупность записей горизонталей или иных изолиний.
Это актуально при решении многих инженерных задач: 1) создание карт и отображение на них рельефа суши 2) задачи вертикальной планировки территории для нужд строительства; 3) гидрологические задачи, мелиорация земель; 4) экологические задачи и др. Основные положения методов решения указанных задач изложены в [1-5].
Автором предложено аналитико-цифровое моделирование [6-13] в виде отдельных алгоритмических модулей [14] при создании цифровой модели рельефа местности, основанных на нелинейных схемах интерполирования отметок между исследуемыми точками.
Цели и задачи
Цель исследования — разработать метод аналитического моделирования поверхности рельефа (АМПР) местности под «нулевой» баланс разработки грунта рассматриваемого участка территории.
Задачи исследования:
- разработать алгоритм определения средне-планировочной отметки рассматриваемой территории;
- формализовать аналитические зависимости исходных структур данных и визуализировать полученные результаты исследования;
Материалы и методы
Воспользуемся локальной системой координат (ЛСК), в виде «правой тройки (0,X,Y,Z)».
Будем искать аналитическо-цифровую модель поверхности рельефа (АМПР), и аналитическую модель средне-планировочной поверхности (СПП), рассматриваемой на рис.1 площадки. как функцию двух переменных:
АМПР = f (№1(по «0Х»), №2 (по «0У»)) (1)
где: указанные в двумерном массиве [ere] черные отметки вдоль оси «0Х», — локальная переменная №1; черные отметки вдоль оси «0У» — локальная переменная №2 искомой аналитической функции.
Что даёт нам поиск аналитических выражений моделей рельефа и планировочной поверхности, как функций от черных отметок в двух направлениях?
Совместное, системное решение полученных аналитических выражений соответствующих поверхностей друг с другом даст возможность алгоритмизации нахождения аналитического выражения линии их пересечения друг с другом, - т.е. аналитического нахождения так называемой линии «нулевых» работ при разработке грунта под «нулевой» баланс, и её последующей оптимизации.
Используем результаты камеральной обработки ситуационного топографического плана местности в виде расчётных "черных" отметок [англ.- existing relief elevation (ere)], приведенных на рис. 1.
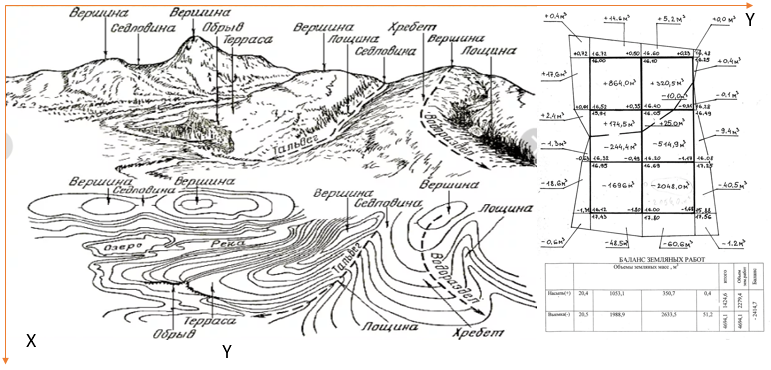
Рис. 1. Вариант топографического плана для работ под «нулевой» баланс
На рис. 1 приведена 50-ти метровая сеточная разметка по направлениям осей «0Х» и «0У» в обоих направлениях.
Результаты исследований 1
Создадим массив «чёрных» отметок, представив их двумерным массивом данных [ere](5х4). Структуру данных в массиве [ere], упорядочим в соответствии с локальной системой координат, — «правой тройкой (0XYZ)». За начало отсчётов (ЛСК) примем левый верхний угол рассматриваемой таблицы.
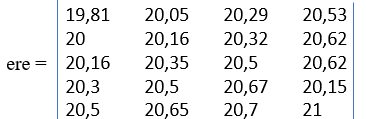
Рис. 2. «Выборка черных отметок» данным в двумерный массив [ere](5х4)
Разработка алгоритма определения средне-планировочной отметки.
На рис. 3 показана последовательная обработка элементов массива [ere]. С помощью вспомогательных переменных е (1,2,3), соответствующих адресаций к кодированным и структурированным данным массива [ere(i,j)], приведенным инструкциям, - вычисляется значение высотной отметки средне-планировочной поверхности «Hm» рассматриваемого участка:

Рис. 3. Алгоритм вычисления средне-планировочной отметки «Hm (n =12)
Результат является средним арифметическим суммы элементов массива данных [ere]
Результаты исследований 2
Таким образом, средне-планировочная отметка для приведенных данных составляет 20,394 м. Эта величина представляет собой высотную отметку «Hz» горизонтальной плоскости в принятой (ЛСК). Следовательно, это такая планировочная поверхность, относительно которой «бóльшим» черным отметкам рельефа будут поставлены в соответствие понятие «выемки», а «меньшим» — понятие «насыпи» при разработке грунта под «нулевой» баланс.
Формализация вывода аналитической модели (АМПР) поверхности рельефа рассматриваемой площадки.
Представим функцию, аппроксимирующую указанный на рис.2 ландшафт полиномом шестой степени, как наиболее подходящую аппроксимацию1 приведенных в массиве [ere] данных.
Функции аппроксимации значений черных отметок (ЛСК) «по оси Х» и «по оси У» рис. 1, будем искать также в виде соответствующих полиномов шестой степени p(х) и p(y).
Суперпозицию функций черных отметок [p(х) и р(у)] обозначим, как аппроксимируемые искомым полиномом «рельефные» отметки поверхности рассматриваемой площадки.
Из анализа структуры данных массива [ere], черные отметки, соответствующие приведенной разметке по осях «0X» и «0Y» (ЛСК), — отличаются друг от друга не на постоянную, а на некую случайную переменную величину отклонения. Нахождение «средних» значений отклонений осуществим с помощью вычисления их «среднего геометрического»2. Такая величина, — наиболее точно соответствует оценке центральной тенденции.
Результаты исследований 3
Аналитическое выражение (АМПР) в виде полинома шестой степени от указанных суперпозиций полиномов шестых степеней p(x) и p(y) представим в виде:
$p(x,y)=\sqrt[2]{p(x)∙p(y)} $ (2)
Представление системы уравнений для p(х) по оси «0X», в которой неизвестными являются коэффициенты полинома p(x) степени шесть, а свободными членами структурированные на рис. 2 элементы массива [ere](5х4) покажем на рис. 3:

Рис. 3. Алгоритм поиска полинома p(x)
где: «Ах», — матрица коэффициентов в рассматриваемом полиноме, «Вх» — вектор свободных членов полинома, — как выборка из массива [ere](5х4) по оси «0Х», «Кх» — результат решения системы уравнений, вектор значений найденных неизвестных.
Вывод уравнения полинома р(x), осуществим с использованием функцию "векторизация"3 результатов решения системы уравнений на рис.3. Покажем выполненные преобразования с векторами «Кх» и «С1» на рис.4:
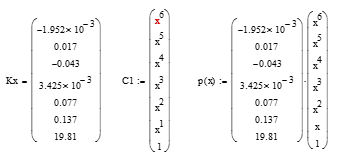
Рис. 4. Операции векторизации полинома p(x)
После преобразований получим искомое аналитическое выражение для полинома p(x) следующего вида:
$p(x)=0,137∙x^1+0,077∙x^2+0,003425∙x^3-0,043∙x^4+0,017∙x^5-0,001952∙x^6+\\19.81$ (3)
Систему уравнений p(y) по оси «0Y», в которой неизвестными являются коэффициенты полинома p(y) степени шесть, покажем на рис. 5:
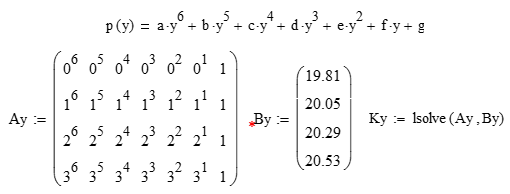
Рис. 5. Алгоритм поиска полинома p(y)
где Аy — матрица коэффициентов в рассматриваемом полиноме, Ву — вектор свободных членов полинома, - выборка из массива [ere] параллельно оси «0у», Кy — результат решения указанной системы, вектор значений найденных неизвестных.
Вывод уравнения полинома p(y) также осуществим, используя функцию "векторизации" результатов решения системы уравнений. Преобразуем вектор «Ky» и «С2», рис. 6:
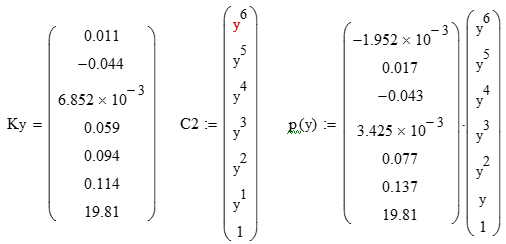
Рис. 6. Операции векторизации полинома p(y)
В результате чего, также получим аналитическое выражение уравнения полинома p(y) шестой степени по оси «0Y», которое в общем виде будет представлять собой:
$p(y)=a∙y^1+b∙y^2+c∙y^3-d∙y^4+e∙y^5-f∙y^6+g$ (4)
а после вычислений по псевдокоду на рис. 6:
$p(y)=0,137∙y^1+0,077∙y^2+0,003425∙y^3-0,043∙y^4+0,017∙y^5-0,001952∙y^6+19.81$ (5)
Графически построим искомую функцию полинома аппроксимации моделирующего поверхность рельефа рассматриваемого участка в заявленном виде (2), как функции суперпозиций переменных р(х) и р(у).
На рис. 7 приведём традиционную форму представления полученных результатов моделирования рельефа поверхности в плане, в традиционной форме — с помощью соответствующих заданному ландшафту изолиниям, рис. 7a.
На рис. 7b покажем графическое представление разработанной модели (АМПР) в виде аналитической функции суперпозиций p(x) и p(y) (2):
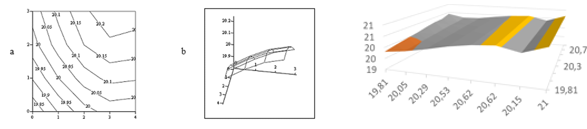
Рис. 7(a, b) a) Разработанная модель рельефа рассматриваемого участка в традиционной форме,
представленная с помощью эквипотенциальных поверхностей уровней, заданных массивом данных [ere](5х4)
b) тоже, в форме модельной объёмной поверхности заданного ландшафта
Покажем процесс вывода аналитической функции средне-планировочной плоскости для определенной ранее отметки «Hm» = 20.394м.
Обобщённо, средне-планировочную поверхность также представим полиномом шестой степени. Функционально, как квадратный корень из суперпозиций функций p0(x) и р0(y). Для этого, поочерёдно, вдоль осей ЛКС «0X» и «0Y» аппроксимируем полученные результаты вычисления средне-планировочной отметки.
Систему уравнений полинома проходящих через максимальное количество заданных топографических точек, координат маccива [ere] вдоль оси «0X», в общем виде представим следующим образом:
$p0(x)=a∙x^1+b∙x^2+c∙x^3-d∙x^4+e∙x^5-f∙x^6+g$ (6)
Запишем систему уравнений по оси «0X», в которой неизвестные представим коэффициентами полинома p0(x), как это показано на рис. 8

Рис. 8. Псевдокод алгоритма вычисления полинома p0(x)
где Ах0, — матрица коэффициентов средне-планировочной поверхности, Вх - вектор свободных членов полинома, Кх0 - результат решения указанной системы, - вектор значений найденных неизвестных. Выполнив "векторизацию" и преобразования с векторами «Кх0» и «С10» получим:
$p0(x)=3,423∙10{-13}∙x^1-2,258∙10{-13}∙x^2-5,678∙10{-13}∙x^3+
+6,28∙10{-13}∙x^4-2,105∙10{-13}∙x^5+2,279∙10{-13}∙x^6+20,394$ (7)
Запишем систему уравнений по оси «0Y», в которой неизвестные представим коэффициентами полинома p0(y) — массивом размером (4х7), рис. 9:

Рис. 9. Алгоритм вычисления полинома p0(y)
где Аy(0) — матриица коэффициентов в рассматриваемом полиноме, В — вектор свободных членов полинома, выборка из матрицы (ere) параллельно оси «0у», Кy0 — результат решения указанной системы, вектор значений найденных неизвестных.
В результате получим:
$p0(y)=2,004∙10{-13}∙y^1-6,13∙10{-14}∙y^2+1,345∙10{-13}∙y^3+
+4,023∙10{-13}∙y^4-3,561∙10{-13}∙y^5+7,059∙10{-14}∙y^6+20,394$ (8)
Результаты исследований 4
Получим функцию полинома от вычисленных переменных для построения средне-планировочной поверхности рассматриваемой площадки, как поверхности "нулевых" работ в виде функции двух переменных р0(х) и р0(у):
$p0(x,y)=\sqrt[2]{p0(x)∙p0(y)} $ (9)
По результатам (10) построим искомую поверхность "нулевых" работ рассматриваемой площадки, рис. 10:
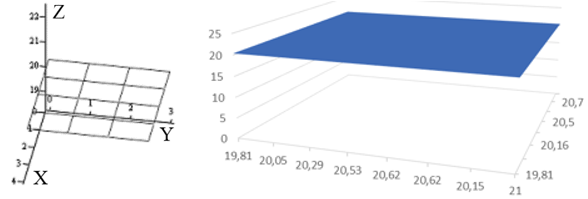
Рис. 10. Модель средне-планировочной на отметке 20,396 м
Заключение
В работе созданы аналитические зависимости моделей поверхности рельефа и средне-планировочная поверхность.
На четвертом этапе совместное системное решение приведенных зависимостей позволяет автоматически ставить в соответствие относительные значения, соответствующие высотным отметкам моделей рельефа поверхности и средне-планировочной поверхности, — значениям объёмов «выемки» и «насыпи» грунта под «нулевой баланс.
Совместное аналитическое решение полученных аналитических зависимостей позволяет получить точное алгебраическое решение линии «нулевых» работ.
Поставленные в работе цели и задачи исследования достигнуты.
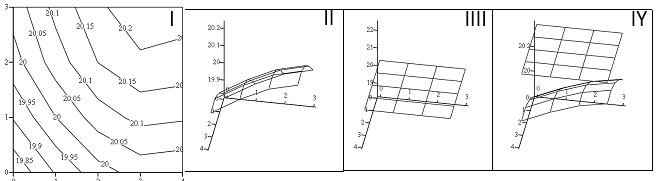
Рис. 11. Визуализация этапов алгоритмизации моделирования рельефа местности под «нулевой» баланс.
I, II, III и IY — этапы алгоритмизации
Примечания
[1] Аппроксимацией представляется приближенное представление сложной (имеющей громоздкое математическое представление) или заданной в виде таблицы функции f(x) более простой функцией q(x), имеющей минимальные отклонения от исходной функции. Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта.
[2] Среднее значение, которое указывает на центральную тенденцию или типичное значение набора чисел, используя произведение их значений при их существенном разбросе значений друг относительно друга.
[3] Векторизация, вид распараллеливания программы вычислений, при котором однотипные приложения, выполняющие одну операцию в каждый момент времени, модифицируются для выполнения нескольких однотипных операций одновременно. Скалярные операции, обрабатывающие по паре операндов, заменяются на операции над массивами (векторами), обрабатывающие несколько элементов вектора в каждый момент времени.
1. Берлянт А. М. Картография: учебник для вузов. - Москва: Аспект Пресс, 2022 - 336 с.
2. Витковский В. В. Картография (теория картографических проекций): монография. - Санкт-Петербург: Лань, 2019 - 473с.
3. Колосова, Н. Н. Картография с основами топографии: учебное пособие для вузов. - Москва: Дрофа, 2021 - 272 с.
4. Плишкина О. В. Практикум по картографии: методическое пособие. - Улан-Удэ: ВСГТУ, 2006 - 64 с. - URL: http://window.edu.ru/resource/705/48705/files/uchpebj9.pdf
5. Черепнин, В. И., Соловьев, А. Н. Прикладные вопросы инженерной геодезии. Часть I. Инженерно-графические работы на топогеодезической карте-(плане): учебное пособие. Санкт-Петербургский лесотехнический университет, 2005 http://window.edu.ru/resource/004/66004
6. Evans I.S. General geomorphometry, derivations of altitude, and descriptive statistics // Spatial Analysis in Geomorphology. L.: Methuen, 1972. - P. 17-90. 1
7. Farr T.G., Hensley S., Rodriguez E. et al. The shuttle radar topography mission // CEOS SAR Workshop. Toulouse 26-29 Oct. 1999. Noordwijk, 2020. P. 361-363
8. Freeman T.G. Calculating catchment area with divergent flow based on a regular grid. Computers & Geosciences, 17(3), 20211. P. 413-422.
9. Fu, P. 2020. A Geometric Solar Radiation Model with Applications in Landscape Ecology. Ph.D. Thesis, Department of Geography, University of Kansas, Lawrence, Kansas, USA.
10. Guzzetti F. Landslide hazard and risk assessment. PhD dissertation. Bonn, Germany, - 2021
11. Hamid N., Ahmad A. Calibration of high resolution digital camera based on different photogrammetric methods. Earth and Environmental Science, 2021 (18). P. 1-6.
12. Hernandez Encinas L., S. Hoya White, A. Martin del Rey and G. Rodriguez Sanchez. Modeling forest fire spread using hexagonal cellular automata. Applied Mathematical Modeling 31(60, 2021). - Р. 1213-1227.
13. Hengl T., Finding the right pixel size. Computers and Geosciences, 2022. 32(9): 1283-1298.
14. Hirshmuller H. Accurate and efficient stereo processing by semi-global matching and mutual information, Computer Vision and Pattern Recognition, 2022. CVPR 2022. IEEE Computer Society Conference, Vol. 2, Р. 807−814. ing, 71 (7), 2022. - Р. 817-823.






















