Москва, г. Москва и Московская область, Россия
Москва, г. Москва и Московская область, Россия
Россия
УДК 531 Общая механика. Механика твердых тел
УДК 624 Строительные конструкции. Подземное строительство. Земляные работы. Фундаменты, основания и их устройство. Строительство тоннелей. Строительство мостов. Строительство наземных сооружений
Известно, что здания и сооружения совершают колебания от ветра, землетрясений, работы различных машин и оборудования. Рассмотрена динамика поведения жилого дома с точки зрения разработки принципов и методов расчета сооружений на воздействие различных динамических нагрузок с целью обеспечение их несущей способности при совместном воздействии статических и динамических нагрузок, а также ограничение уровня колебаний для исключения вредного влияния колебаний на людей и на технологические процессы. В статье проанализировано ветровое воздействие на 25 этажное здание, рассмотрены параметры региональных и локальных ветров, Рассмотрены основные аспекты определения ветровых нагрузок на здания и сооружения. Исследован характер ветровой нагрузки, а также методы ее расчета. предусмотрена задача дальнейшего развития метода расчета ветрового воздействия с использованием компьютерного моделирования.
ядро жесткости. железобетонный каркас, метод конечных элементов, лестнично-лифтовый узел, расчетная схема, сбор нагрузок, снеговая нагрузка, ветровая нагрузка
Актуальность работы
В многоэтажных зданиях при определении усилий в вертикальных несущих элементах большую роль играет ветровая нагрузка, которая к тому же является динамической. Для того чтобы разгрузить вертикальные элементы, а также ограничить горизонтальные перемещения и колебания здания, в конструктивную схему вводят дополнительные конструкции. В зданиях с железобетонным каркасом для этих целей служат продольные и поперечные железобетонные стены, объединенные в так называемое ядро жесткости, которое размещается как правило в лестнично-лифтовом узле. Вопрос размещения ядра жесткости в лестнично-лифтовом узле (ЛЛУ)заключается в том, что несмотря на очевидную выгоду размещения его в центре здания с конструктивной точки зрения, ЛЛУ размещается в крайнем пролете в связи с требованиями пожарной безопасности по устройству незадымляемых путей эвакуаций т.е. лестниц. В данной работе исследовано на сколько влияет и влияет ли вообще различное расположение ядра жесткости на усилия в колоннах, а также на горизонтальные перемещения и колебания здания.
Цели и задачи
Для проведения исследования были смоделированы два 25-этажных здания с железобетонным каркасом с одним подземным этажом, единственным отличием которых является расположение ядра жесткости.
Расчет проводился методом конечных элементов (МКЭ). Диски перекрытий и стены были смоделированы универсальным прямоугольным элементом оболочки (КЭ 41), данный КЭ имеет 6 степеней свободы в каждом узле и хорошо подходит для моделирования плит и стен. Колонны, универсальным пространственным стержневым конечным элементом (КЭ 10). Толщина перекрытий и стен принята 200 мм, модуль упругости принят как для бетона В30 (Е=32 000 МПа) с учетом понижающих коэффициентов для вертикальных конструкций – 0.6 и горизонтальных конструкций 0.2, коэффициент Пуассона принят равным 0.2. Сечение колонн 800х400 мм. модуль упругости принят как для бетона В30 (Е=32 000 МПа) с учетом понижающего коэффициента для вертикальных конструкций – 0.6, коэффициент Пуассона равен 0.2. Также был смоделирован один подземный этаж, помимо основных несущих конструкций в подземном этаже были смоделированы наружные железобетонные стены толщиной 200 мм. Расположенные по контуру. Конструкция здания опирается на монолитную фундаментную плиту толщиной 800 мм. В связи с тем, что основной целью данной работы было сравнение усилий в вертикальных элементах от ветровой нагрузки в зданиях с различным положением ядра жесткости учет работы грунтового основания нецелесообразен. В связи с этим на узлы фундаментной плиты были наложены связи обеспечивающие жесткое защемление фундамента.
На рис. 1 показаны рассматриваемые конструктивные решения.
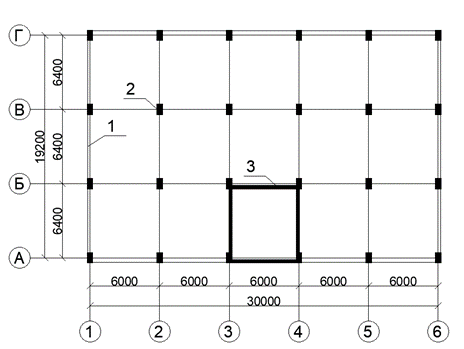
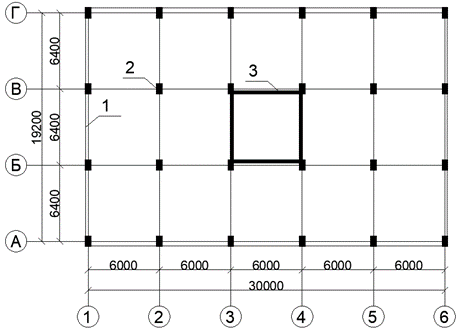
Рис 1. Расположение несущих конструкций типового этажа рассматриваемых вариантов.
1- контур плиты толщиной 200 мм., 2- колонны сечением 800х400 мм., 3- стены - 200 мм.
Сбор нагрузок
Нагрузка от собственного веса железобетонных конструкций была задана автоматически, с учетом коэффициента надежности по нагрузке gf =1.1.
Сбор нагрузок от собственного веса полов здания представлен в таблице 1.
Таблица 1
|
Нагрузки на перекрытия |
|||||
|
№ п/п |
Наименование, толщина слоя, мм |
Вид нагрузки |
Нормативная нагрузка, кПа |
gf |
Расчетная нагрузка, кПа |
|
1 |
Керамогранитная плитка, 10 |
Постоянная |
0,24 |
1,2 |
0,29 |
|
2 |
Клеевая основа, 5 |
Постоянная |
0,09 |
1,3 |
0,12 |
|
3 |
Цементно-песчанная стяжка, 35 |
Постоянная |
0,63 |
1,3 |
0,82 |
|
|
Итого |
|
0,96 |
1,28 |
1,23 |
Нормативное значение полезной нагрузки на типовой этаж здания принято согласно таблице 8.3 СП 20.13330.2016 равному Pt = 1.5 кПа. С учетом коэффициента надежности по нагрузке gf =1.3 (пункт 8.2.7 СП 20.13330.2016) расчетное значение полезной нагрузки принимается равным 1.95 кПа.
Полезная нагрузка прикладывается к плите покрытия как равномерно распределенная.
Нормативное значение снеговой нагрузки определяется по формуле 10.1 СП 20.13330.2016:
где:
μ- коэффициент формы;
се – коэффициент учитывающий снос снега с покрытия;
сt – термический коэффициент;
Sg – Нормативное значение веса снегового района (для Москвы принимается 1.5 kN);
Расчетное значение снеговой нагрузки с учетом коэффициента надежности по нагрузке gf =1.4 (пункт 10.12 СП 20.13330.2016) принимается равным 2.1 kN.
Снеговая нагрузка прикладывается к плите покрытия как равномерно распределенная.
Ветровая нагрузка
Согласно современным нормативным документам, полная ветровая нагрузка на здание складывается из средней wm и пульсационной wg составляющей.
Значение средней ветровой нагрузки определяется по формуле 11.2 СП 20.13330.2016:
где:
w0 – нормативное значение ветрового давления (для Москвы 0.23 кПа);
с- аэродинамический коэффициент (принимаемый равным для наветренной и подветренной стороны 0.8 и 0.5)
k(ze) – коэффициент учитывающий изменение ветрового давления по высоте, определяется по формуле 11.3 СП 20.13330.2016:
![]()
Коэффициенты k10 и a принимаются по таблице 11.3 СП 20.13330.2016 в зависимости от типа местности (принимаем тип местности (В)).
Коэффициент ze принимается согласно пункту 11.1.5 СП 20.13330.2016 случай (В).
Расчетное значение ветровой нагрузки с учетом коэффициента надежности gf =1.4 для различных высот представлены в таблице 1.
Таблица 1.
Значения ветровой нагрузки
|
Зона действия нагрузки |
Ze |
Wm при с=0.8, кПа |
Wm при с=0.8, кПа |
|
0 < H < 31.5 м |
30 |
1,08 |
0,67 |
|
31.5 м < H < 34.5 м |
33 |
3,31 |
2,07 |
|
34.5 м < H < 37.5 м |
36 |
6,32 |
3,95 |
|
37.5 м < H < 40.5 м |
39 |
10,22 |
6,38 |
|
40.5 м < H < 43.5 м |
42 |
15,09 |
9,43 |
|
43.5 м < H < 47.5 м |
45 |
21,05 |
13,16 |
|
47.5 м < H < 75 м |
75 |
68,83 |
43,02 |
Общая схема действия ветровой нагрузки показана на рис. 2.
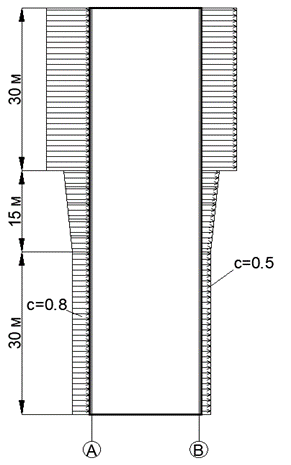
Рис. 2. Схема распределения ветровой нагрузки
Значение средней составляющей ветровой нагрузки умножается на грузовую площадь и прикладывается к торцевым узлам плит перекрытия. Для корректного учета полной ветровой нагрузки (в том числе пульсационной) необходимо назначить тип нагрузки для средней составляющей «Неактивное», далее необходимо создать динамическое загружение и назначаем параметры пульсационной нагрузки. Далее присваиваем для динамического загружения тип «Мгновенное». В таком случае полная ветровая нагрузка учитывается корректно программным комплексом при расчете.
Давление грунта на стены подземной части здания
Боковое давление грунта (расчетное значение) на наружные стены подземной части здания при нагрузке на поверхность земли у стен здания р=10 kN/м2.
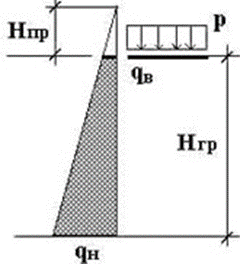
Рис 3. К определению бокового давления грунта на стены подземной части здания Объемный вес насыпного грунта составляет gгр=18 kN/м3, угол внутреннего трения j=300.
Высота приведенного слоя грунта: Нпр= р/gгр=10/18=0,56 м,
Верхнее значение на трапециевидной эпюре бокового давления грунта:
qв = gf ×gгр× Hпр × tg2 (45°- j /2) =1,15×18×0,56×0,33=3,83 kN/м2,
Нижнее значение на трапециевидной эпюре бокового давления грунта:
qн = gf× gгр ×(Hпр+Нгр)×tg2 (45°- j /2) =1,15×18×(2,5+0,56)× 0,33=20,9 kN/ м2
Давление грунта прикладывается к стенам подвала трапециевидной нагрузкой.
После приложения всех нагрузок в программном комплексе необходимо задать Таблицы расчетного сочетания нагрузок (РСН) и расчетного сочетания усилий (РСУ). Таблица РСУ генерируется автоматически с учетом коэффициентов сочетаний для различных типов нагрузки. Согласно нормативно-технической документации, коэффициент сочетания для постоянных нагрузок равен Ψ=1.0, коэффициент сочетания для длительных нагрузок равен Ψ=1.0 для основной по влиянию нагрузки и Ψ=0.95 для остальных. Коэффициенты сочетаний для кратковременных нагрузок равен Ψ=1.0 для основной по влиянию нагрузки, Ψ=0.9 для второй и Ψ=0.7 для остальных нагрузок. Помимо сочетаний нагрузок необходимо назначить группы взаимоисключающих нагрузок, в данном случае взаимоисключающими являются ветровые воздействия, действующие в разных направлениях.
Таблица РСН составляется вручную. Главное ее отличие от таблицы РСУ является, то что РСН используют для определения перемещений. Так как перемещения определяются от нормативных нагрузок, а мы задавали их расчетными необходимо коэффициенты сочетания нагрузок разделить на коэффициенты надежности по нагрузке.
Перед расчетом необходимо упаковать схему, чтобы исключить возможные удвоения узлов и элементов.
Результаты исследований
Эпюры моментов, полученные в результате расчета двух зданий представлены на рис. 4.
а)

б)
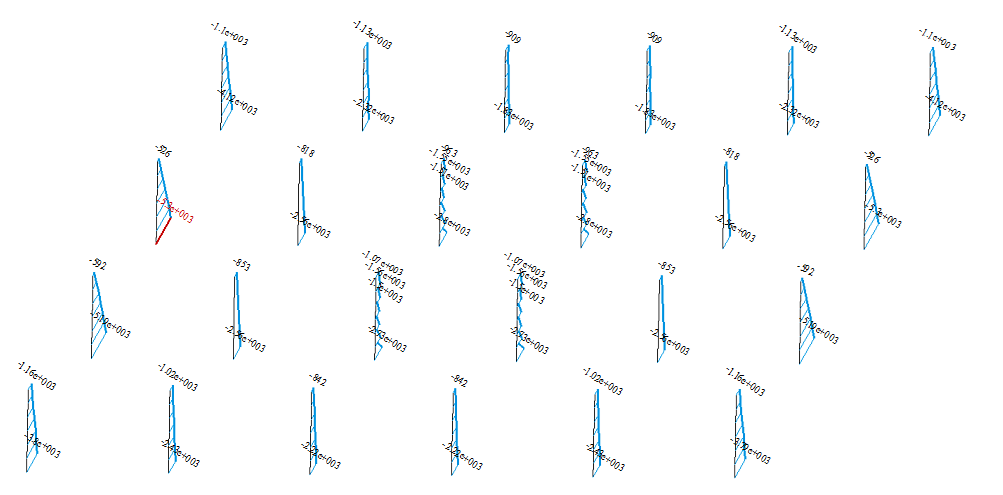
Рис. 4. Эпюры моментов в колоннах 1-го этажа (а –вариант 1, б – вариант 2)
Как следует из рис. 4, максимальный момент находится в колонне крайнего ряда и равен 5380 kNм. в схеме «а» и 5298 kNм. в схеме «б». Данное различие (всего 1.5 %) несущественно).
Эпюры продольных усилий, полученные в результате расчета двух зданий представлены на рис. 5.
а)
б)
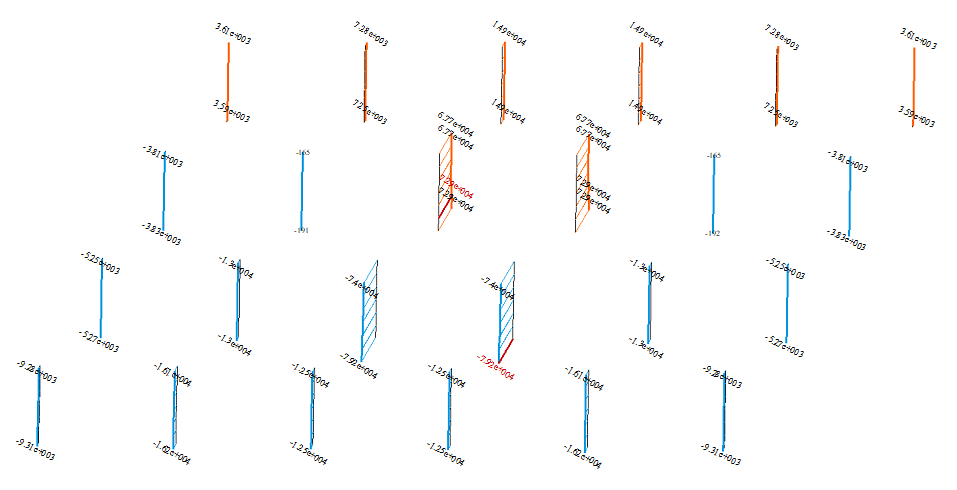
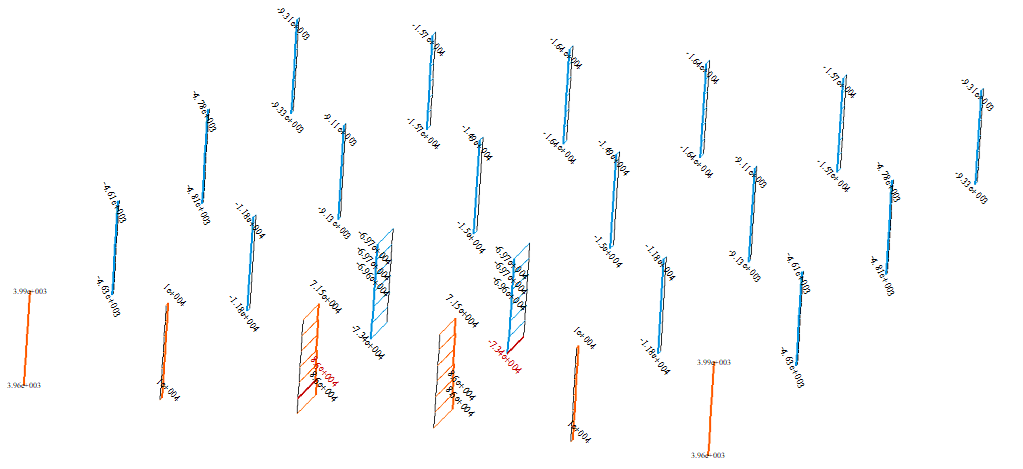
Рис. 5. Эпюры продольных сил в колоннах 1-го этажа (а –вариант 1, б – вариант 2)
Наибольшее растягивающее усилие в схеме «а» составляет 73400 kN, сжимающее 86000 kN при этом наиболее загруженными колоннами оказались те, которые примыкают к ядру жесткости. В схеме «б» наибольшее растягивающее усилие составило 72900 kN, сжимающее 79200 kN. Разница составляет около 8%. При этом стоит отметить, что усилия в колоннах примыкающих к ядру жесткости в несколько раз выше чем в остальных колоннах, это свидетельствует о том, что ядро жесткости воспринимает большую часть нагрузки, и существенно разгружает другие конструкции.
Горизонтальные перемещения, полученные в результате расчета двух зданий представлены на рис. 6.
а)
б)
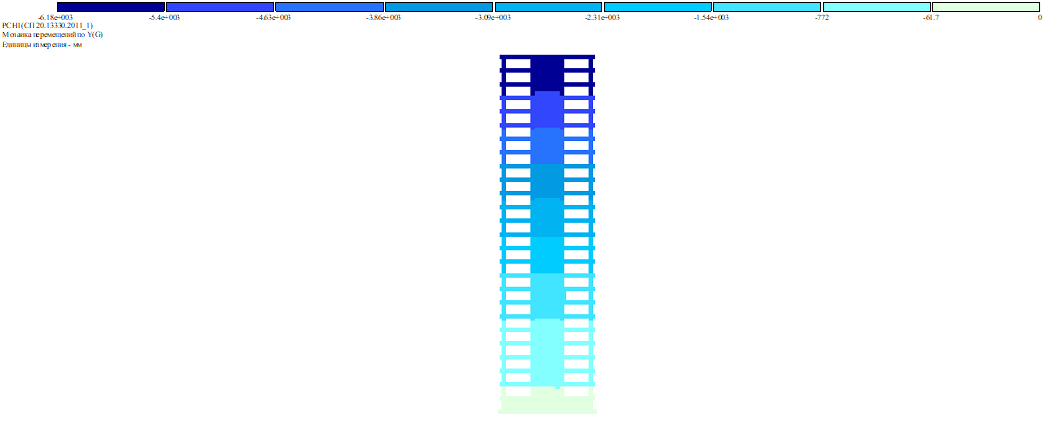
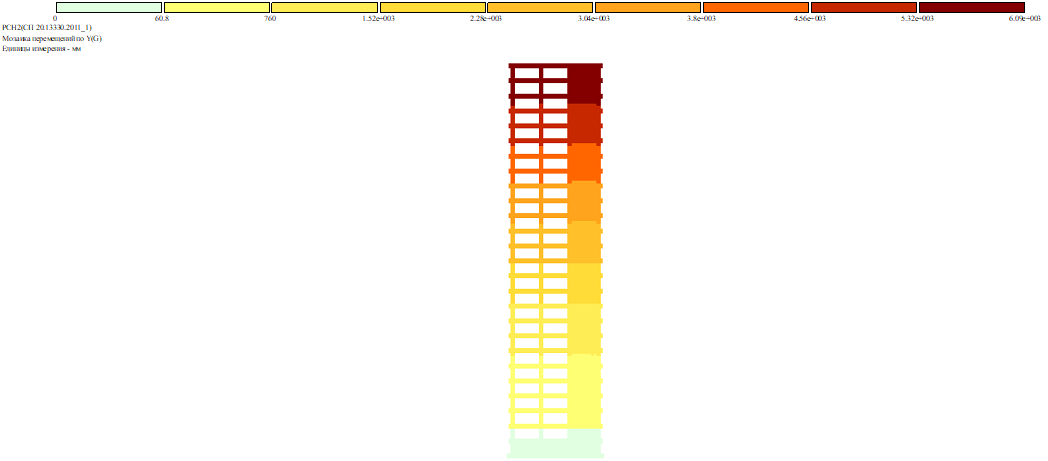
Рис. 6. Горизонтальные деформации (а –вариант 1, б – вариант 2)
Выводы.
- Максимальное перемещение составляет для случая «а» 6090 мм, для случая «б» 6180 мм.
- Большие значения перемещения вызваны тем, что для здания такой конфигурации (высота 75 метров, ширина 20 метров) недостаточно устройства ядра жесткости только в ЛЛУ, необходимо вводить дополнительные диафрагмы жесткости, однако они могли помешать оценить влияние расположения ядра жесткости и поэтому вводится не стали.
Очевидно, из выше приведенных сравнений, перенос ЛЛУ, а вместе с ним и ядра жесткости здания в крайний пролет, а вместе с ним и ядра жесткости здания в крайний пролет и наоборот, - не оказывает большого влияния на работу конструкции.
1. Гордееев В.Н., Лантук-Дященко А.И., Пашинский В.А., Перельмутер А.В., Пичугин С.Ф. Нагрузки и воздействия на здания и сооружения. M.: ASV, 2007. 482 с.
2. Лычев А.С. Надежность строительных конструкций. M.: АСВ, 2008. 184 с.
3. Райзер В.Д. Теория надежности в строительном проектировании. M.: АСВ, 1998. 304 с.
4. Барштейн М.Ф. Динамический расчет высоких сооружений на действие ветра. Справочник по динамике сооружений. M.: Стройиздат, 1972. С. 286-321.
5. Барштейн М.Ф. Руководство по расчету зданий и сооружений на действие ветра M.: Стройиздат,1978. 120 с.
6. Беспрозванная И.М., Соколов А.Г., Фомин Г.М. Воздействие ветра на высокие сплошностенчатые сооружения M.: Стройиздат, 1976. 185 с. (rus)
7. Болотин В.В. Методы теории вероятностей и теории надежности в расчетах сооружений. M.: Стройиздат, 1982. 351 с.
8. Коренев Б.Г., Рабинович И.М. Динамический расчет зданий и сооружений. M.: Стройиздат, 1984. 303 с.
9. Бронштейн М.Ф., Бородачев Н.М., Блюмина Л.К. Динамический расчет на специальные воздействия. M.: Стройиздат, 1981. 215 с.
10. Реттер Е.И., Стриженов С.И. Аэродинамика зданий. M.: Стройиздат, 1968. 240 с.
11. Реттер Е.И. Архитектурно-строительная аэродинамика. M.: Стройиздат. 1984. 296 с. (rus)
12. Савицкий Г.А. Ветровая нагрузка на сооружения. M.: Стройиздат, 1972. с. (rus)
13. Симиу Е., Сканлан Р. Воздействие ветра на здания и сооружения. M.: Стройиздат, 1984. 360 с. (rus)
14. Дубинский С.И. Численное моделирование ветровых воздействий на высотные здания и комплексы. M.: 2010. 198 с. (rus)
15. Bitsuamlak G.T., Stathopoulos T., Bedard C. Numerical evaluation of turbulent flows over complex terrains. A review//Journal of Aerospace Engineering, 17(4), 2004. Pp. 135-145.
16. Blocken V., Stathopoulos T., Carmeliet J. CFD simulation of atmospheric boundary layer-wall function problems//Atmospheric Environment, 41 (2), 2007. Pp. 238-252.


















