Казань, Республика Татарстан, Россия
Предложена методика оптимизация опор в виде усеченных конических оболочек со ступенчатым изменением толщины стенки. В качестве критериев оптимизации выбраны потенциальная энергия деформации, максимальное перемещение конструкции и первая частота собственных колебаний. Решение выполняется с использованием методов нелинейной оптимизации в сочетании с методом конечных элементов в среде Matlab.
оптимизация, коническая оболочка, переменная толщина, метод конечных элементов
Formulation of the problem. This article discusses a technique for optimizing shell structures in the form of a truncated cone with a stepwise varying thickness h. Such structures act as supports for wind turbines. When solving the optimization problem, the load acting on the tower is simplified by us in the form of the concentrated unit force at the upper end (Fig. 1). This load simulates an upstream wind turbine. The support of the tower at the base is assumed to be hingedly fixed.
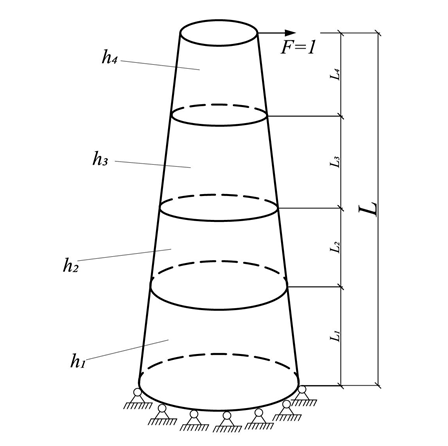
Fig. 1. Design scheme of the structure
The following values act as the objective function:
- Potential energy of deformation (PED) of the structure W;
- Maximum displacement of the structure vmax.
- The first frequency of natural vibrations of the structure ω.
The choice of PED as an objective function is justified by the fact that it is an integral measure that determines the level of the stress-strain state [1]. The lower the PED value is, the better the system resists to external influences [2].
The choice of the maximum displacement of the structure as an optimization criterion does not require additional explanations. The first frequency of natural vibrations was chosen as the objective function, since it shows the ability of a structure to resist the occurrence of the phenomenon of mechanical resonance: the higher it is, the more difficult it is to cause resonance during forced vibrations.
The structure consists of n steps with heights Li and wall thicknesses hi. It is required to find such values of Li and hi, to ensure the optimal value of the objective function. The optimum for the potential energy of deformation and displacement corresponds to the minimum, and for the first frequency to the maximum. In this case, the volume of the construction material must be constant and equal to the specified value. In addition to the restriction on the constancy of the volume, there is one more obvious restriction in this problem: ![]()
Methods. The problem posed belongs to the class of nonlinear optimization problems. Its solution is carried out in the Matlab software package using the Optimization Toolbox package. The interior point method [3] is used as an optimization method. To calculate the objective functions, a program based on the finite element method was prepared. The structure is modeled by flat triangular shell finite elements with 6 degrees of freedom at the node. It is based on the relations given in [4]. After solving the system of FEM equations, the potential strain energy is determined by the formula:
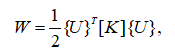
where [K] – stiffness matrix, {U} – vector of the nodal displacements.
The first natural frequency is determined from the equation:
![]()
where [M] is the mass matrix.
Results and Discussion. The problem was solved for the shell with height L = 40 m, with radii R0 = 2.15 m and R1 = 1.3 м. As an initial step, we took a structure of constant thickness h = 15 mm. Objective function values are W = 0.157 J, vmax = 0.314 mm, ω = 18.4 s-1. Let us first consider the solution for the number of steps n = 2. Lower (lb) and upper boundaries (ub) for the varied parameters are given in Table 1.
The results of solving the optimization problem are summarized in Table 2. When using the criteria of minimum PED and minimum displacement, the same optimal values of varied parameters were obtained. A similar result was obtained earlier in [5,6] when optimizing reinforced concrete slabs. Compared to the structure with constant thickness, the potential energy of deformation and displacement are reduced by about 7%. Also, the first natural frequency is increased by 29%.
Table 1. Lower and upper boundaries of the varied parameters at n = 2
|
parameter |
L1, m |
h1, mm |
h2, mm |
|
lb |
10 |
5 |
5 |
|
ub |
35 |
40 |
40 |
The variant corresponding to the maximum of the first frequency, from the point of view of the potential energy of deformation and maximum displacement, turned out to be worse than the initial step. The maximum of the first frequency is reached at the lower boundary of the parameter h2.
Table 2. Optimal parameters of the conical shell with two sections and the corresponding values of the objective functions
|
Criterion |
L1, m |
h1, mm |
h2, mm |
W, J |
vmax, mm |
ω, s-1 |
|
Minimum PED, minimum displacement |
29.1 |
17.2 |
7.3 |
0.146 |
0.293 |
23.8 |
|
First frequency maximum |
19.46 |
23.2 |
5 |
0.185 |
0.371 |
32.1 |
Let us consider further the solution for the number of steps n = 3. The number of variable parameters increases from 3 to 5. The lower and upper boundaries for the variables L1, L2, h1, h2, h3 are given in Table 3. Optimal values of parameters L1, L2, h1, h2, h3 found on the basis of three criteria are given in Table 4.
The solutions obtained by the criterion of minimum PED and minimum displacement are slightly different, but provide almost the same values of the functions W and vmax. Compared to the constant thickness structure, the potential strain energy and maximum displacement reduced by 8.3% and 8.6%, respectively.
Table 3. Lower and upper boundaries of the varied parameters at n = 3
|
parameter |
L1, m |
L2, m |
h1, mm |
h2, mm |
h3, mm |
|
lb |
1 |
1 |
5 |
5 |
5 |
|
ub |
35 |
35 |
40 |
40 |
40 |
Table 4. Optimal parameters of the conical shell and the corresponding values of the objective functions when dividing the structure into 3 sections
|
Criterion |
L1, m |
L2, m |
h1, mm |
h2, mm |
h3, mm |
W, J |
vmax, mm |
ω, s-1 |
|
minimum PED |
19.04 |
10.18 |
18.7 |
13.8 |
7.3 |
0.144 |
0.288 |
25.3 |
|
minimum displacement |
21.33 |
10.92 |
18.4 |
12.5 |
6.1 |
0.144 |
0.287 |
25.4 |
|
first frequency maximum |
14.67 |
7.58 |
25.4 |
11.9 |
5 |
0.175 |
0.351 |
33.1 |
Conclusions. A technique has been developed to optimize wind turbine towers in the form of truncated conical shells with a stepwise change in thickness based on the criteria of the minimum potential energy of deformation, the minimum of displacement and the maximum of the first vibration frequency. The optimal relationships between the dimensions of the steps and the wall thicknesses have been found. It was found that the criteria for the minimum PED and minimum displacement lead to practically the same results. With an increase in the number of steps, it is possible to improve the values of the objective functions.
1. Васильков Г.В. Эволюционные задачи строительной механики: синергетическая парадигма. Ростов н/Д: ИнфоСервис, 2003. 179 с.
2. Васильков Г.В. Теория адаптивной эволюции механических систем / Г.В. Васильков. Ростов н/Д: Терра-Принт, 2007. 248 с.
3. Byrd R. H., Hribar M. E., Nocedal J. An interior point algorithm for large-scale nonlinear programming //SIAM Journal on Optimization. 1999. Т. 9. №. 4. С. 877-900.
4. Чепурненко А.С., Сайбель А.В., Савченко А.А. Конечно-элементное моделирование ползучести пластин произвольной формы // Инженерный вестник Дона. 2017. №1. URL: http://ivdon.ru/ru/magazine/archive/n1y2017/3998
5. Ефименко Е.А., Беккиев М.Ю., Маилян Д.Р., Чепурненко А.С. Определение оптимального расположения опор в плите перекрытия промышленного здания с использованием стохастических методов // Вестник Дагестанского государственного технического университета. Технические науки. 2020. № 1. С. 138-146.
6. Efimenko E.A., Chepurnenko A.S., Mailyan D.R., Saibel A.V. The industrial buildings reinforced concrete floor slabs with rational choice of the column pitch // IOP Conference Series: Materials Science and Engineering. 2020. Vol. 896. URL: https://iopscience.iop.org/article/10.1088/1757-899X/896/1/012004/pdf


















