с 01.09.2014 по настоящее время
Казанский (Приволжский) федеральный университет (Институт дизайна и пространственных искусств, Главный научный сотрудник)
Батайск, Ростовская область, Россия
Ростов на Дону, Ростовская область, Россия
Россия
УДК 62 Инженерное дело. Техника в целом. Транспорт
ГРНТИ 67.03 Инженерно-теоретические основы строительства
ГРНТИ 67.01 Общие вопросы строительства
ОКСО 01.04.03 Механика и математическое моделирование
ББК 38 Строительство
ББК 308 Монтаж, эксплуатация, ремонт машин и промышленного оборудования
ТБК 5013 Техническая механика. Сопротивление материалов
В статье приводится вывод разрешающих уравнений для расчета трехслойных цилиндрических оболочек при осесимметричном нагружении с учетом ползучести. Задача сводится к системе из двух обыкновенных дифференциальных уравнений. Решение выполняется численно при помощи метода конечных разностей в сочетании с методом Эйлера.
трехслойные оболочки, ползучесть, метод конечных разностей, деформации поперечного сдвига
Трехслойные конструкции в виде пластин и оболочек находят широкое применение в различных отраслях, включая строительство, кораблестроение, авиастроение и т.д. Такие конструкции сочетают в себе малый вес и высокую жесткость. В качестве среднего слоя трехслойных конструкций широко используются полимерные материалы, для которых помимо упругих свойств характерна явно выраженная реология, поэтому для их расчета необходимо подключать аппарат теории ползучести.
Рассмотрим трехслойную цилиндрическую оболочку, находящуюся под действием гидростатического давления (рис. 1).
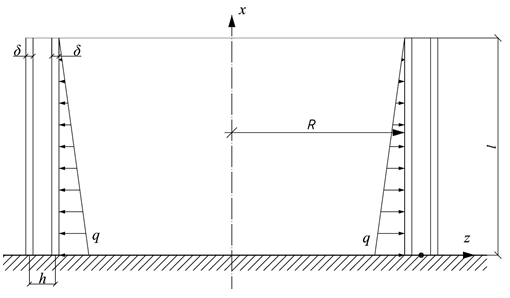
Рис. 1. Осесимметрично нагруженная трехслойная цилиндрическая оболочка
Геометрические уравнения получим из общих уравнений Коши в цилиндрических координатах, имеющих вид [1]:
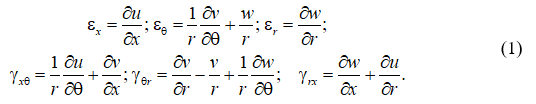
Для получения геометрических уравнений цилиндрической оболочки в (1) следует положить r = R + z и учесть, что z<<R. Деформации обшивок при этом примут вид:
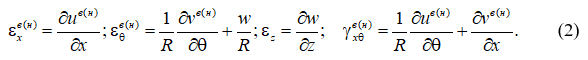
Деформации сдвига среднего слоя запишутся в виде:
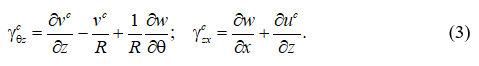
Для перемещений u среднего слоя примем линейное распределение по толщине:
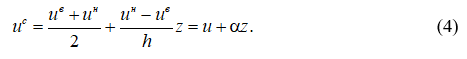
Перемещения  при осесимметричном нагружении отсутствуют. Деформации сдвига заполнителя из (3) и (4) запишутся в виде:
при осесимметричном нагружении отсутствуют. Деформации сдвига заполнителя из (3) и (4) запишутся в виде:

Касательные напряжения в заполнителе с учетом ползучести определяются следующим образом:
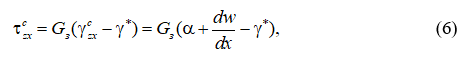
где ![]() – деформации ползучести среднего слоя,
– деформации ползучести среднего слоя, ![]() – деформации сдвига заполнителя.
– деформации сдвига заполнителя.
Деформации обшивок при осесимметричном нагружении запишутся в виде:
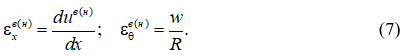
Принимая гипотезу о равномерном распределении касательных напряжений по толщине заполнителя, поперечную силу ![]() запишем следующим образом:
запишем следующим образом:
![]()
Связь между напряжениями и деформациями для обшивок запишется в виде:
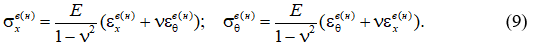
Принимая, что изгибающий момент ![]() полностью воспринимается обшивками, представим его в виде:
полностью воспринимается обшивками, представим его в виде:
![]()
где 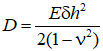 – цилиндрическая жесткость трехслойной оболочки.
– цилиндрическая жесткость трехслойной оболочки.
Осевые усилия ![]() также полностью воспринимаются обшивками:
также полностью воспринимаются обшивками:
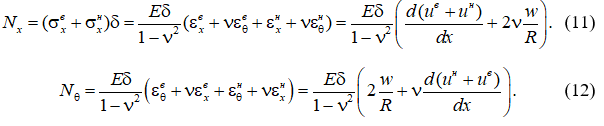
Приравнивая усилие ![]() к нулю и выражая величину
к нулю и выражая величину ![]() через прогиб, получим следующую формулу для
через прогиб, получим следующую формулу для ![]() :
:

Уравнения равновесия при осесимметричном нагружении запишутся в виде [1]:
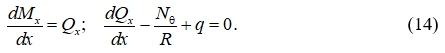
Нагрузка q в случае действия гидростатического давления определяется по формуле:
![]()
где ![]() – удельный вес жидкости.
– удельный вес жидкости.
Подставляя (10) и (8) в первое уравнение равновесия в (14), получим:
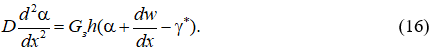
Подставив (8) и (13) во второе уравнение равновесия в (14), получим:
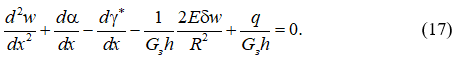
Таким образом, задача расчета трехслойной цилиндрической оболочки при осесимметричном нагружении свелась к системе из двух дифференциальных уравнений (16) и (17) относительно функций ![]() .
.
Для жестко защемленной в основании оболочки граничные условия имеют вид:
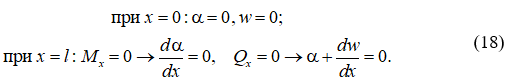
Решение системы уравнений (16) и (17) может быть выполнено численно методом конечных разностей в сочетании с методом Эйлера для определения деформаций ползучести [2].
Был выполнен расчет оболочки с пенополиуретановым заполнителем при следующих исходных данных: l = 3 м, R = 2 м, G = 4.85 МПа, Е = 2·105 МПа, ν = 0.3, h = 8 см, γ = 10 кН/м3, δ = 1 мм. В качестве закона ползучести использовалось нелинейное уравнение Максвелла-Гуревича, имеющее вид [3]:
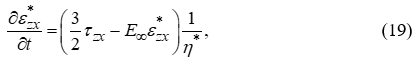
где 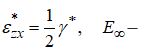 модуль высокоэластичности,
модуль высокоэластичности, ![]() – релаксационная вязкость, которая нелинейно зависит от напряжения:
– релаксационная вязкость, которая нелинейно зависит от напряжения:
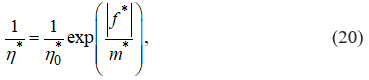
где ![]() – начальная релаксационная вязкость,
– начальная релаксационная вязкость, ![]() – модуль скорости,
– модуль скорости, ![]() – функция напряжений.
– функция напряжений.
Реологические параметры пенополиуретана [4]: ![]() ,
, ![]() .
.
На рис. 2 приведен полученный в результате расчета график изменения максимальной величины прогиба w. Из представленного графика видно, что ползучесть среднего слоя не оказывает заметного влияния на перемещения оболочки. Аналогичные результаты были получены автором ранее в работе [5] для пологих трехслойных оболочек.
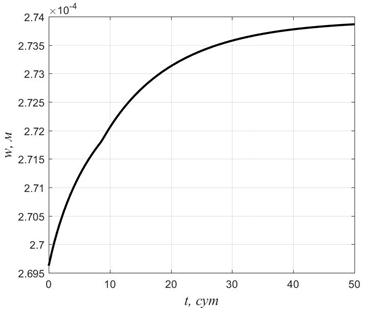
Рис. 2. Изменение во времени максимальной величины прогиба оболочки
Из рис. 3, показывающего изменение во времени максимальных касательных напряжений в заполнителе, видно, что в среднем слое происходит релаксация напряжений. Изгибающие моменты ![]() также убывают во времени, что демонстрирует рис. 4. Поскольку кольцевая сила пропорциональна прогибу w, то она во времени постоянна. Таким образом, в целом ползучесть среднего слоя положительно сказывается на напряженно-деформированном состоянии рассматриваемой конструкции.
также убывают во времени, что демонстрирует рис. 4. Поскольку кольцевая сила пропорциональна прогибу w, то она во времени постоянна. Таким образом, в целом ползучесть среднего слоя положительно сказывается на напряженно-деформированном состоянии рассматриваемой конструкции.
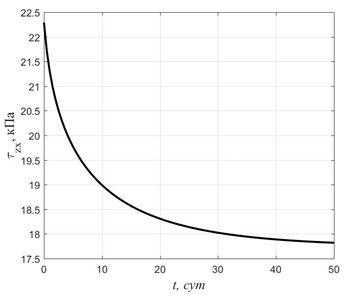
Рис. 3. Изменение во времени наибольших касательных напряжений в заполнителе
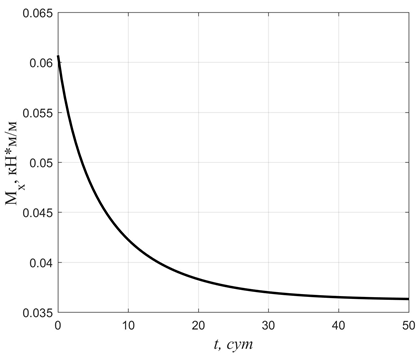
Рис. 4. Изменение во времени максимальной величины изгибающего момента Mx
1. Самуль, В.И. Основы теории упругости и пластичности / В.И. Самуль. - М.: Высшая школа, 1982. - 264 с.
2. Литвинов, С.В. Плоская деформация неоднородных многослойных цилиндров с учетом нелинейной ползучести / С.В. Литвинов, С.Б. Языев С.Б. Языева // Вестник МГСУ. - 2010. - № 1. - С. 128-132.
3. Литвинов, С.В. Устойчивость полимерных стержней при различных вариантах закрепления / С.В. Литвинов, Е.С. Клименко, И.И. Кулинич, С.Б. Языева // Вестник МГСУ. - 2011. - № 2-2. С. 153-157.
4. Yazyev, B.M. Calculation of Three-Layer Panels with Polyurethane Foam Filler Taking into Account the Rheological Properties of the Middle Layer / B.M. Yazyev, A.S. Chepurnenko, A.A. Savchenko // Materials Science Forum. - 2018. - Vol. 935. - Pp. 144-149.
5. Андреев, В.И. Расчет трехслойной пологой оболочки с учетом ползучести среднего слоя / В.И. Андреев, Б.М. Языев, А.С. Чепурненко, С.В. Литвинов // Вестник МГСУ. - 2015. - № 7. - С. 17-24.




















